A symbolic moment of joining up the dots of historypublished at 13:41 BST
Sean Coughlan
Royal correspondent, reporting from the Vatican
We’re inside the Basilica of St Paul’s Outside the Walls and
it is absolutely massive, even…

Sean Coughlan
Royal correspondent, reporting from the Vatican
We’re inside the Basilica of St Paul’s Outside the Walls and
it is absolutely massive, even…

We simulate the dynamics of VCG pools using a kinetic simulation that is based on the Gillespie algorithm. In the simulation, oligomers can hybridize to each other to form complexes or dehybridize from an existing complex. Moreover, two oligomers can undergo templated ligation if they are hybridized adjacent to each other on a third oligomer. At each time , the state of the system is determined by a list of all single-stranded oligomers and complexes as well as their respective copy number. We refer to the state of the system at the time as the ensemble of compounds . Given the copy numbers, the rates of all possible chemical reactions can be computed. To evolve the system in time, we need to perform two steps: (i) We sample the waiting time until the next reaction, , from an exponential distribution with mean , and update the simulation time, . (ii) We pick which reaction to perform by sampling from a categorical distribution. Here, the probability to pick reaction equals . The copy numbers are updated according to the sampled reaction, yielding . Steps (i) and (ii) are repeated until the simulation time reaches the desired final time, . A more detailed explanation of the kinetic simulation is presented in Göppel et al., 2022; Rosenberger et al., 2021.
Our goal is to compute observables characterizing replication in the VCG scenario based on the full kinetic simulation. In the following derivation, we focus on one particular observable (yield) for clarity. The results for other observables are stated directly, as their derivations follow analogously. Recall the definition of the yield introduced in the Results section,
As we are interested in the initial replication performance of the VCG, we compute the yield based on the ligation events that take place until the characteristic timescale of ligations . In principle, we would like to compute the yield based on the templated ligation events that we observe in the simulation. Unfortunately, for reasonable system parameters, it is impossible to simulate the system long enough to observe sufficiently many ligation events to compute to reasonable accuracy. For example, for a VCG pool containing monomers at a total concentration of and VCG oligomers of length at a total concentration of , it would take about 1700 hr of simulation time to reach (Figure 8). Multiple such runs would be needed to estimate the mean and the variance of the observables of interest, rendering this approach unfeasible.
The total concentration of feedstock monomers equals , while the total concentration of VCG oligomers is . The energy contribution per matching nearest-neighbor block is set to . The volume of the system is varied, and the time evolution is simulated until . The runtime of the simulation scales linearly with the volume of the system.
Instead, we compute the replication observables based on the copy number of complexes that could potentially perform a templated ligation, that is complexes in which two strands are hybridized adjacent to each other, such that they could form a covalent bond. We can show analytically that the number of productive complexes is a good approximation for the number of incorporated nucleotides: The number of incorporated nucleotides can be computed as the integral over the ligation flux, weighted by the number of nucleotides that are added in each templated ligation reaction,
Here, denotes the copy number of the complex C in the pool . and denote the lengths of the oligomers that undergo ligation, and is an indicator function which enforces that only complexes in a ligation-competent configuration contribute to the reaction flux. As only a few ligation events are expected to happen until , it is reasonable to assume that the ensembles do not change significantly during . Therefore, the integration over time may be interpreted as a multiplication by ,
(6)
where denotes the average over realizations of the ensembles within the time interval . This average corresponds to the average number of complexes in a ligation-competent configuration. Note that, at this point, we made the additional assumption that no templated ligations are taking place between . This assumption is reasonable, as (i) the equilibration process is very short compared to the characteristic timescale of ligation, and (ii) the number of complexes that might allow for templated ligation during equilibration is lower than in equilibrium (we start the simulation with an ensemble of single-stranded oligomers). Both aspects imply that the rate of templated ligation is negligible during the interval .
In order to compute the average over different realizations of ensembles (as required in Equation 6), we need to sample a set of uncorrelated ensembles that have reached the hybridization equilibrium, which can be done using the full kinetic simulation. The simulation starts with a pool containing only single-stranded oligomers and reaches the (de)hybridization equilibrium after a time . We identify this timescale of equilibration by fitting an exponential function to the total hybridization energy of all complexes in the system, (Figure 9A). In the set of ensembles used to evaluate the average in Equation 6, we only include ensembles for time to ensure that the ensembles have reached (de)hybridization equilibrium. To ensure that the ensembles are uncorrelated, we require that the time between two ensembles that contribute to the average is at least . The correlation time, , is determined via an exponential fit to the autocorrelation function of (Figure 9B). Besides computing the expectation value (Equation 6), we are also interested in the ‘uncertainty’ of this expectation value, that is in the standard deviation of the sample mean . (We use as a short-hand notation for ). The standard deviation of the sample mean, , is related to the standard deviation of , , by the number of samples, . Moreover, based on the van-Kampen system size expansion, we expect the standard deviation of to be proportional to , such that .

(A) The equilibration timescale is determined based on the total hybridization energy of all strands in the pool, . By fitting an exponential function to , we obtain a characteristic timescale (vertical dotted line), which is then used to calculate the equilibration time as (vertical dashed line). The horizontal dashed line shows the total hybridization energy expected in (de)hybridization equilibrium according to the coarse-grained adiabatic approach (Methods). (B) The correlation timescale is determined based on the autocorrelation of . We obtain (vertical dashed line) by fitting an exponential function to the autocorrelation. In both panels, we show simulation data obtained for a VCG pool containing monomers and VCG oligomers with a concentration of as well as oligomers of length with a concentration of .
Using Equation 6 (as well as an analogous expression for the number of nucleotides that are incorporated in VCG oligomers), the yield can be expressed as
The additional condition in the numerator ensures that the product oligomer is long enough to be counted as a VCG oligomer, that is at least nucleotides long. Analogously, the expression for the fidelity of replication reads
Multiplying fidelity and yield results in the efficiency of replication,
The ligation share of a particular type of templated ligation , that is, the relative contribution of this templated-ligation type to the nucleotide extension flux, can be represented in a similar form as the other observables,
As all observables are expressed as the ratio of two expectation values, , we can compute the uncertainty of the observables via Gaussian error propagation,
Since the variances, and , as well as the covariance, , are proportional to , the standard deviation of the observable mean, , scales with the inverse square root of the number of samples and the system volume, that is . Therefore, the variance of the computed observable can be reduced by either increasing the system volume or increasing the number of samples used for averaging. Both approaches incur the same computational cost: (i) Increasing the number of samples, , requires running the simulation for a longer duration, with the additional runtime scaling linearly with the number of samples. (ii) Similarly, the additional runtime needed due to increased system volume, , also scales linearly with (Figure 8). One update step in the simulation always takes roughly the same amount of runtime, but the change in simulation time per update step depends on the total rate of all reactions in the system. The total rate is dominated by the association reactions, and their rate is proportional to the volume. Therefore, the change in simulation time per update step is proportional to . The runtime, which is necessary to reach the same simulation time in a system with volume as in a system with volume 1, is a factor of longer in the larger system. With this in mind, it makes no difference whether the variance is reduced by increasing the volume or the number of samples. For practical reasons (post-processing of the simulations is less memory- and time-consuming), we opt to choose a moderate number of samples, but slightly higher system volumes to compute the observables of interest. The simulation parameters (length of oligomers, concentrations, hybridization energy, volume, number of samples, characteristic timescales) used to obtain the results presented in Figure 2 are summarized in Table 1.
| VCG oligo. length | conc. ratio | volume | equilibration time | correlation time | number of samples | yield | efficiency |
|---|---|---|---|---|---|---|---|
| 6 | 1.0 ⋅ 10−4 | 5.0 ⋅ 104 | 3.4 ⋅ 106 | 1.9 ⋅ 106 | 3805 | 0.04 ± 0.01 | 0.04 ± 0.01 |
| 6 | 1.0 ⋅ 10−3 | 5.0 ⋅ 103 | 1.2 ⋅ 107 | 2.6 ⋅ 106 | 3264 | 0.38 ± 0.02 | 0.36 ± 0.02 |
| 6 | 3.3 ⋅ 10−3 | 8.0 ⋅ 102 | 1.3 ⋅ 107 | 2.7 ⋅ 106 | 5400 | 0.68 ± 0.02 | 0.64 ± 0.02 |
| 6 | 1.0 ⋅ 10−2 | 9.1 ⋅ 101 | 1.4 ⋅ 107 | 2.7 ⋅ 106 | 5440 | 0.87 ± 0.01 | 0.77 ± 0.03 |
| 6 | 3.3 ⋅ 10−2 | 9.1 ⋅ 100 | 1.3 ⋅ 107 | 2.4 ⋅ 106 | 6170 | 0.96 ± 0.01 | 0.63 ± 0.03 |
| 7 | 1.0 ⋅ 10−4 | 3.9 ⋅ 104 | 1.7 ⋅ 108 | 2.6 ⋅ 107 | 784 | 0.33 ± 0.05 | 0.33 ± 0.05 |
| 7 | 1.0 ⋅ 10−3 | 7.6 ⋅ 102 | 1.9 ⋅ 108 | 4.0 ⋅ 107 | 2041 | 0.87 ± 0.02 | 0.81 ± 0.05 |
| 7 | 3.3 ⋅ 10−3 | 7.7 ⋅ 101 | 1.9 ⋅ 108 | 3.3 ⋅ 107 | 2980 | 0.95 ± 0.01 | 0.87 ± 0.04 |
| 7 | 1.0 ⋅ 10−2 | 1.1 ⋅ 101 | 1.9 ⋅ 108 | 2.6 ⋅ 107 | 3465 | 0.99 ± 0.01 | 0.81 ± 0.05 |
| 7 | 3.3 ⋅ 10−2 | 1.7 ⋅ 100 | 1.9 ⋅ 108 | 3.1 ⋅ 107 | 3235 | 0.99 ± 0.04 | 0.73 ± 0.05 |
| 8 | 1.0 ⋅ 10−4 | 6.3 ⋅ 103 | 2.5 ⋅ 109 | 1.1 ⋅ 108 | 466 | 0.81 ± 0.05 | 0.81 ± 0.05 |
| 8 | 1.0 ⋅ 10−3 | 9.9 ⋅ 101 | 1.9 ⋅ 109 | 3.6 ⋅ 108 | 615 | 0.99 ± 0.01 | 0.99 ± 0.01 |
| 8 | 3.3 . 10-3 | 1.6 ⋅ 101 | 1.0 ⋅ 109 | 2.2 ⋅ 108 | 1100 | 0.95 ± 0.03 | 0.95 ± 0.03 |
| 8 | 1.0 . 10-2 | 3.8 ⋅ 100 | 5.6 ⋅ 108 | 1.4 ⋅ 108 | 1700 | 1.00 ± 0.01 | 0.93 ± 0.05 |
| 8 | 3.3 . 10-2 | 0.9 ⋅ 100 | 4.9 ⋅ 108 | 7.4 ⋅ 107 | 3195 | 1.00 ± 0.03 | 0.82 ± 0.05 |
A human has outkissed one of Google’s superpowered artificial intelligence systems. The achievement isn’t in the realm of romance, however. Instead, this win is in the intellectual realm of advanced mathematics. While largely conceptual in…

While there is plenty of romance in Nobody Wants This Season 2, the platonic relationships — from Joanne and Morgan’s sisterly highs and lows to Esther’s budding friendship with the pair to Joanne and Esther’s tumultuous…

Use this guide to help you get ready for matchday.
Fans are reminded to show…

Saturn isn’t the only planet in our solar system with a ring system. While Saturn’s rings are the most dramatic, the three other gas giants — Jupiter, Neptune, and Uranus — each have a ring system as well. But the fun doesn’t stop there….

 BBC
BBCLincoln City has been fined £8,500 by the Football Association (FA) after supporters aimed “sectarian chants” at an opposition player.
The FA said the club had failed to…

– Advertisement –
ISLAMABAD, Oct 23 (APP): Federal Minister for Religious Affairs Sardar Muhammad Yousuf on Thursday said the government is taking steps to improve land and sea routes for pilgrims, mulling to introduce new system of ferry…
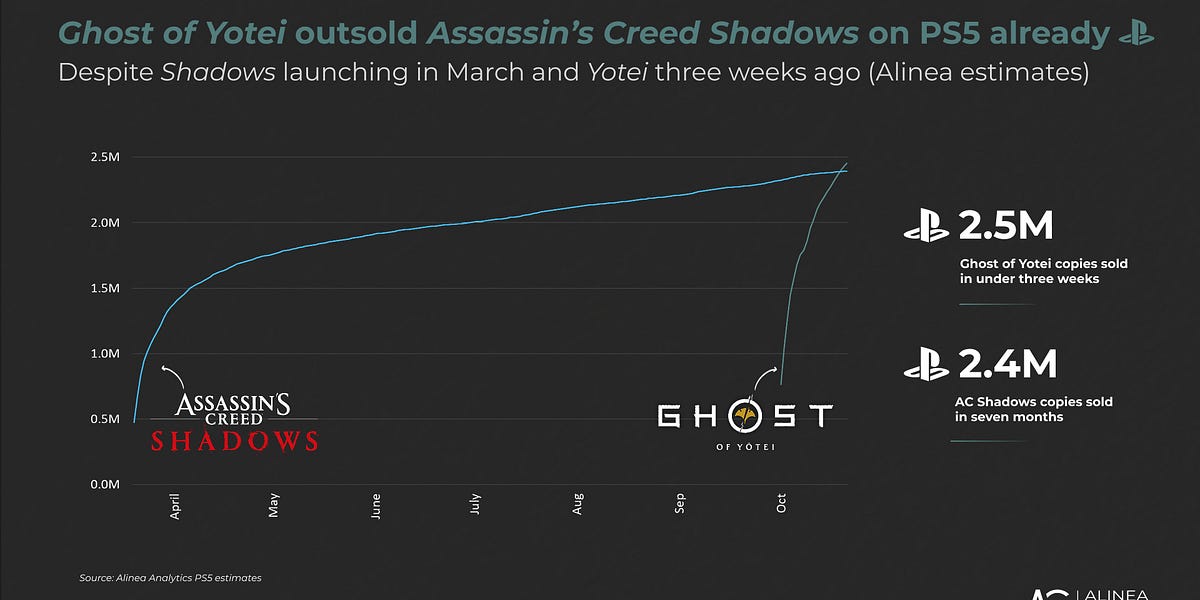
After seven months on the market, Assassin’s Creed Shadows has sold less on PS5 (2.4M) than Ghost of Yotei did (2.5M) in under three weeks, showing that this samurai showdown is just about settled.
Across all platforms, Shadows performed well in…