Information dynamics and the emergence of high-order individuality in ecosystems

Here, we discuss the details of the model and the information-theoretic measures used for the simulation and subsequent analysis of the model. We provide a brief overview of the Tangled Nature model²⁵, followed by the information individuality framework²¹ and other information dynamics measures presented above.

The model

In the Tangled Nature model, species—represented by a binary vector—form the dynamical units of evolution. The binary vector is an abstract representation of the pangenome of the species. The number of agents with the same pangenome represents the population of the species. The model does not assign distinct genomes to each member; therefore, species (identified by distinct binary vectors) act as the primary unit of interaction in the model. Agents from these individual species are subject to three stochastic processes: asexual replication, mutations, and annihilation. No structured groups or hierarchies are defined a priori. The evolutionary dynamics occur in a space of pangenomes where random interactions connect different species. The probability that an agent reproduces is determined by a sum over influences from other co-existing species the agent interacts with. This simple mathematical model captures a broad range of evolutionary phenomena. Starting with a few existing species, the model dynamics evolves to a quasi-stable configuration (also known as quasi evolutionary stable strategies or q-ESS) where only a select group of species exist. These subsets of species with stable populations are disrupted by mutations in the system that drive them to extinction, and a new group of species emerges as a result of the reorganization. Over time, the system evolves to more and more stable configurations, where the durations of the metastable states increase³⁰ and the interactions between the existing subset of species become more mutualistic over time^28,56, thus avoiding these extinction events and developing resilience.

Although the model has evolved into different variations over the years, for this study, we consider the model as defined in the original paper³⁰. Each species is determined using a unique binary pangenome vector of length L, comprising an ecosystem of a total of M = 2^L possible species. Interactions between species are encoded in an interaction matrix J_M×M. All entries in the interaction matrix are sampled at random from a uniform distribution, ({J}_{i,j} sim {{{mathcal{U}}}}(-1,1)), thus allowing potentially symbiotic, competitive or predator-prey relationships between any pair of species. However, of all possible interactions, each interaction is permitted with the coupling probability Θ. The coupling probability controls the overall connectivity of the interaction matrix. The population of a given species at a given time is represented as n_i(t), and the total population of the ecosystem is represented as N(t).

Starting from a random initial condition, where only a subset of species exist in the system, each timestep starts with an annihilation step in which a member of a species, selected uniformly at random, is killed with a probability p_kill. This is followed by asexual reproduction, where a member of a species, selected uniformly at random, creates an offspring with probability p_off. Each element of the pangenome of the offspring undergoes a mutation with a probability p_mut. These mutations introduce new species in the ecosystem, which then interact with the existing species. Since the population of species is updated using a random selection of an agent at each timestep, a sufficient number of updates are needed to ensure each agent is updated at least once. Therefore, the state of the system is recorded after each generation, i.e. N(t)/p_kill timesteps, which is the average number of timesteps required to kill all currently existing species. The reproduction probability p_off depends upon the fitness of the species at the given timestep. The fitness function, which is a weighted sum of interactions with all other species, is defined as

where the parameter μ relates to the inverse of the carrying capacity of the ecosystem. It characterizes the impact of resource constraints driven by increasing population N(t), which negatively contributes to fitness. Meanwhile, k is a scaling parameter for the strength of the interactions. The interaction strength is calculated using the sum of the influences from neighbouring species J_i,j, weighted by their corresponding populations n_j. Thus, the fitness of a given species depends not only on how it interacts with other neighbouring species but on the population of the ecosystem as well. The fitness function is related to the reproduction probability p_off for a given species i at timestep t as

Note that the probability of reproduction is non-linearly related to the fitness function. Although the probability of reproduction is higher for species with positive fitness, some non-zero probability of reproduction exists for negative fitness values, which enables non-performing species to reproduce and mutate towards fitter species. We visualize the fitness (({{{mathcal{H}}}})) and reproduction probability (p_off) values in an example of interacting species (see Fig. 8)

For the purposes of our study, the fixed parameters used for the model are L = 10, Θ = 0.25, p_kill = 0.2, k = 33 and μ = 1/143. These parameters are chosen based on the standard parameter ranges used in previous studies³⁰ that have recreated intermittent co-evolutionary dynamics observed in fossil records⁶³. We study the changes observed in the dynamics of the model when a key parameter p_mut is varied. This parameter represents the selection pressure introduced by the ecosystem. Since changing temperature and weather conditions lead to more mutations^38,39, p_mut can be considered a proxy for controlling abiotic environmental selection pressures⁵⁷. This parameter has a significant impact on the dynamics of the system: visually, it can be observed (see Fig. 2) that the dynamics are more selective and stable with fewer transitions at very low mutation rates (p_mut = 0.001). In an intermediate range (p_mut = 0.01), more species are observed during the metastable states, along with more transitions. As the mutation rate increases in the transition region, the transition time between two metastable states increases throughout this range. Finally, for very high mutation rates (p_mut≥ 0.05), new species emerge, old species die every generation, and the metastable states are non-existent (i.e. no stable population of species emerge). Thus, the system exhibits a phase transition where the system moves from order to disorder between the range of p_mut ∈ (0.4, 0.5) (see ref. ⁶³ for a detailed discussion).

Computationally efficient Rust code was used to simulate the Tangled Nature Model. The code is available with documentation on GitHub.

Information-theoretic measures

In this paper, we use tools from information theory to estimate the various measures presented in the Results. Primarily, we use multivariate mutual information (MI) to quantify interdependencies between time series of species populations obtained from the simulations. Typically, the numerical estimation of MI requires stationary probability distributions of the random variables. However, the Tangled Nature model exhibits non-stationary evolution, i.e. the distribution of population across species changes with generational time. Therefore, we use ensembles of simulations to estimate mutual information at each time point. The population distributions are estimated across ensembles at each generational timestep, providing statistically stable empirical distributions for the estimation of MI. This method is commonly used in neuroimaging studies where brain activity changes in time in response to a stimulus⁶⁴. Details of this ensemble method of estimating mutual information are provided in Supplementary Information C. Below, we briefly discuss the measure of information individuality, as well as other measures used to quantify species-environment interactions.

We use the Gaussian estimators from the Java Information Dynamics Toolkit⁶⁵. A Python implementation of these estimators on a subset of simulations generated using the Tangled Nature Model is available on GitHub.

Information individuality

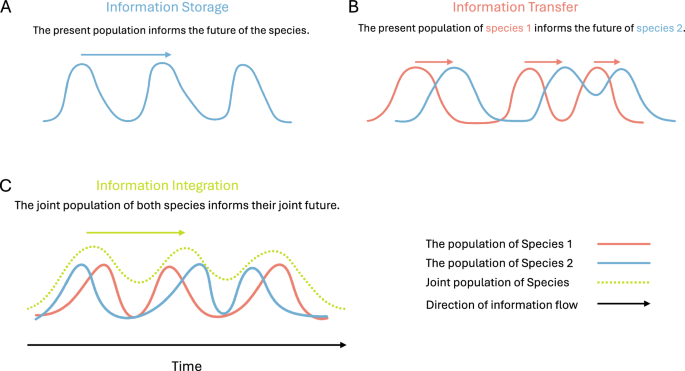
In recent work, Krakauer and others²¹ put forward an information-theoretic solution to identifying the boundary between an individual and their environment. This definition is based on principles of optimal self-prediction- i.e. if a subsystem can predict its future better than any of its parts, and any addition to the subsystem hinders its predictability, then that subsystem is deemed an information individual. This optimal self-predictability enables biological entities to control and navigate their environment⁶⁶, implying that selection for persistence^10,11 could be a putative explanation for their emergence. Once such a boundary is identified, the rest of the parts can be considered as the complement or the environment of the individual. This partition between the individual and the environment is an informational boundary²¹. Therefore, it should not be conflated with the natural environment, which includes abiotic factors not modelled in this study.

For the analyses above, let S(t) be a joint vector representing the population of a subset of K species, S(t) = (n₁(t), n₂(t), …, n_K(t)), at a given time t. Where n_i(t) is the population of the species i. If N(t) is the total population of the ecosystem, the population of the corresponding environment E(t) can then be written as

Then, based on the properties laid out in the original paper²¹, Krakauer et al. propose three different individuality measures as follows:

The operator I(X; Y) refers to the mutual information between variables X and Y. The organismal individuality A^* measures the total information shared between the current population vector S(t) to the future S(t + 1) of the subset of species. Essentially, it tracks how the joint probability distribution of the population of a subset of species evolves over time. The colonial individuality A focuses on the extra information that is shared between the present and the future of the species beyond what can be gained from the environment E(t). Finally, nC measures the information shared between the future population of the subset of species and the present population of the environment beyond what is already known from the present population of the species. Here, we focus on the organismal individuality, which is closely linked to persistence selection^10,11. This individuality measure includes both the collective predictive information of the group of species, as well as the redundancy they share with the environment (see ref. ²¹ for more details). Such information is useful for the species to maintain cohesion and respond to environmental fluctuations.

For our analyses, we first generate an ensemble of 10,000 simulations of the Tangled Nature model with different initial conditions for each mutation rate. We then sample a maximum of 10⁵ different subsets of K species from a rank-ordered list of all possible subsets of species. The subsets are ranked in the order of population of species they contain, starting with the subset of the most populous K species. The rank ordering of subsets of species ensures sampled subsets with similar population distributions and interaction structures across time, improving comparison across different subset sizes. Finally, we measure the average organismal individuality of each subset by estimating the mutual information between the current and future populations of the species (see Supplementary Information C). This process is repeated for different K values ranging from K = 1–15. To account for the bias introduced by increasing dimensions as we calculate multivariate mutual information, we normalize using the group size (see Supplementary Information D). Thus, the normalized individuality score shown in Fig. 4 can be written as

Information transfer and integration

Finally, we briefly describe the measures shown in Section ‘Interaction between species and their environment’ to quantify species-environment interaction. We keep the same notation as above, using S(t) to denote the vector representing the population of K species at time t, and E(t) to denote the state of their environment at time t.

Transfer Entropy (TE) is a conditional mutual information (CMI)-based measure of Granger causality. TE quantifies information transfer from a source variable to the target as CMI between the past of the source and the future of the target conditioned on the past of the target. For instance, TE from a subset S of K species to their environment E can be written under the Markov condition as,

Measures of integrated information (generally denoted by Φ) were first introduced by Tononi et al.⁶⁷ to measure integration among different regions in the brain. Since then, multiple related measures have been proposed, with some adapted to more practical scenarios^31,68 and applied to quantify interactions across a broad range of complex systems³². In essence, these measures quantify the extent to which the interactions between parts of a system drive the joint temporal evolution of the system as a whole; a system has high integrated information if its dynamics strongly depend on the interactions between its parts.

Here, we estimate two measures of integrated information (whole-minus-sum integrated information, Φ^WMS31, and its revised version, Φ^R69) between a single species and its environment jointly evolving over time. Denoting the population of species i and its environment E by the joint random variable X = (n_i, E), Φ^WMS is given by

where X_i denotes the i^th element of X.

Despite its intuitive formulation, Φ^WMS has one crucial disadvantage: it can become negative in systems where the parts are highly correlated^69,70. To address this problem, Mediano et al. proposed a revised measure of integrated information, Φ^R, based on the mathematical framework of integrated information decomposition (ΦID)⁶⁹. This revised measure simply adds a new term to Φ^WMS, correcting for the correlation, or redundancy⁷¹, between the parts of the system:

In the main text, we report results using Φ^R, due to its better interpretability. For completeness, we provide a comparison between the two measures of integrated information in Supplementary Information Fig. F.1.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.