Datasets collection
To comprehensively verify the effectiveness and universality of the proposed algorithm, this study adopts two large-scale public MIDI datasets. First, the LAKH MIDI v0.1 dataset (https://colinraffel.com/projects/lmd/) is used as the main training data. It is a large-scale dataset containing over 170,000 MIDI files, and its rich melody, harmony, and rhythm materials provide a solid foundation for the model to learn music rules. In the data preprocessing stage, this study filters out piano music MIDI files from the LMD dataset because their melodic structures are clear, making them suitable as basic training materials for melody generation models.
However, to address the limitation of the LAKH MIDI dataset being dominated by piano music and test the model’s universality across a wider range of instruments, this study introduces a second multi-instrument dataset for supplementary verification. It adopts the MuseScore dataset (https://opendatalab.com/OpenDataLab/MuseScore), which is a large-scale, high-quality dataset collected from the online sheet music community MuseScore. The core advantage of this dataset lies in its great instrumental diversity, covering sheet music from classical orchestral music to modern band instruments (such as guitar, bass, drums) and various solo instruments. This provides an ideal platform for testing the model’s ability to generate non-piano melodies.
For both datasets, a unified preprocessing workflow is implemented:
1) Instrument Track Filtering: For the LAKH MIDI dataset, this study uses its metadata to filter out MIDI files with piano as the primary instrument. For the MuseScore dataset, which contains complex ensemble arrangements, it applies heuristic rules to extract melodic tracks: prioritizing tracks in MIDI files where the instrument ID belongs to melodic instruments (such as violin, flute, saxophone, etc.) and which have the largest number of notes and the widest range.
2) Note Information Extraction: This study uses Python’s mido library to parse each MIDI file. From the filtered tracks, it extracts four core attributes of each note: Pitch (i.e., MIDI note number, 0-127); Velocity (0-127); Start Time (in ticks); and Duration (in ticks).
3) Time Quantization and Serialization: To standardize rhythm information, it quantizes the start time and duration of notes to a 16th-note precision. This means discretizing the continuous time axis into a grid with 16th notes as the smallest unit, where all note events are aligned to the nearest grid point. All note events are strictly sorted by their quantized start time to form a time sequence.
4) Feature Engineering and Normalization: To eliminate mode differences, each melody is transposed to C major or a minor, allowing the model to focus on learning relative interval relationships rather than absolute pitches. Finally, each note event is encoded into a numerical vector. A typical vector might include: [normalized pitch, quantized duration, interval time from the previous note]. The sequence formed by these vectors serves as the final input to the model.
5) Data Splitting: All preprocessed sequence data are strictly divided into training and test sets in an 80%/20% ratio.
Experimental environment and parameters setting
To ensure the efficiency of the experiment and the reliability of the results, this paper has carefully designed the experimental environment and parameter settings. The experiment uses a high-performance computing cluster equipped with NVIDIA Tesla V100 GPUs to accelerate the model training process. This GPU has strong parallel computing capabilities and can effectively handle the computational burden brought by large-scale datasets. The model training is implemented based on the TensorFlow 2.0 framework, and Keras is used to construct and optimize the neural network structure. Due to the large scale of the LMD dataset, the training process requires a large amount of time and computational resources. Therefore, multi-GPU parallel computing technology is adopted in the experiment. Through multi-GPU parallel computing, the training time can be significantly shortened, and the experimental efficiency can be improved. In addition, the hyperparameters of the model have been carefully adjusted and optimized in the experiment to ensure that the model can achieve the best performance during the training process. Table 2 displays the parameter settings.
In hyperparameter tuning, a combination of Grid Search and manual fine-tuning based on validation set performance is adopted. The tuning method involved dividing 10% of the training set into a Validation Set, with the selection of all hyperparameters ultimately judged by the model’s F1 score on this validation set.
Search space and selection reasons for key hyperparameters:
1) Learning Rate: Searched within the range of [1e-3, 1e-4, 5e-5]. Experiments showed that a learning rate of 1e-3 led to unstable training with severe oscillations in the loss function, while 5e-5 resulted in excessively slow convergence. The final choice of 1e-4 achieved the best balance between convergence speed and stability.
2) Batch Size: Tested three options: [32, 64, 128]. A batch size of 128, though the fastest in training, showed slightly decreased performance on the validation set, possibly getting stuck in a poor local optimum. A batch size of 64 achieved the optimal balance between computational efficiency and model performance.
3) Number of LSTM Layers: Tested 1-layer and 2-layer LSTM networks. Results indicated that increasing to 2 layers did not bring significant performance improvement but instead increased computational costs and the risk of overfitting.
4) Number of Neurons: Tested hidden layer neuron counts in [128, 256, 512]. 256 neurons proved sufficient to capture complex dependencies in melodic sequences, while 512 neurons showed slight signs of overfitting.
5) Reward Function Weights: Tested weight ratios of artistic/technical aspects in [0.5/0.5, 0.7/0.3, 0.9/0.1]. Through subjective listening evaluation of generated samples, the ratio of 0.7/0.3 was deemed to best balance the melodic pleasantness and technical rationality.
Performance evaluation
To evaluate the performance of the constructed model, the proposed AC-MGME model algorithm is compared with the model algorithm proposed by DQN, MuseNet32, DDPG33 and Abouelyazid (2023), and the Accuracy, F1-score, and melody generation time are evaluated. The results in LAKH MIDI v0.1 dataset are shown in Figs. 4, 5 and 6.
Accuracy results for music melody prediction by various algorithms in the LAKH MIDI v0.1 dataset.
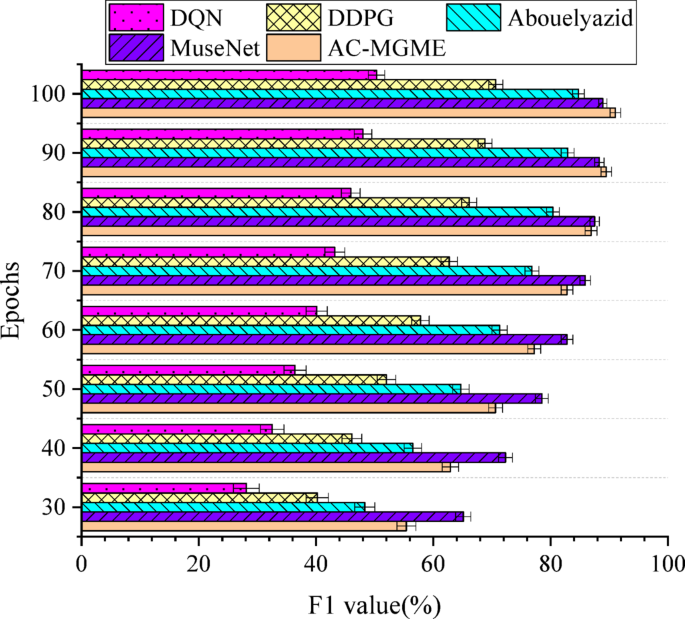
F1-score results for music melody prediction by various algorithms in the LAKH MIDI v0.1 dataset.
In Figs. 4 and 5, it can be found that on the LAKH MIDI dataset, the proposed AC-MGME model algorithm achieves the highest scores in both key indicators: accuracy (95.95%) and F1 score (91.02%). From the perspective of the learning process, although the Transformer-based State-of-the-Art (SOTA) model MuseNet shows strong competitiveness in the early stage of training, the AC-MGME model, relying on its efficient reinforcement learning framework, demonstrated greater optimization potential and successfully surpassed MuseNet in the later stage of training. This not only proves the superiority of its final results but also reflects its excellent learning efficiency. At the same time, AC-MGME maintained a leading position in all stages compared with other reinforcement learning-based comparison models (such as DDPG, DQN, etc.).
To more rigorously verify whether the leading advantage of the AC-MGME model in accuracy is statistically significant, a two-sample t-test is conducted on the results of each model in the final training epoch (Epoch 100). The significance level (α) adopted is 0.05, that is, when the p-value is less than 0.05, the performance difference between the two models is considered statistically significant, as shown in Table 3.
In Table 3, the test results clearly demonstrate that the performance advantage of the AC-MGME model over all comparison models in terms of the key accuracy indicator is statistically significant. Specifically, even when compared with the powerful benchmark model MuseNet, its p-value (0.021) is far below the 0.05 significance threshold, and the differences from models such as DDPG and DQN are even more pronounced (p < 0.001). This conclusion is further confirmed by the F1 score, which more comprehensively reflects the model’s precision and recall. AC-MGME is also significantly superior to all comparison models in terms of F1 score (all p-values are less than 0.05). Overall, these statistical test results fundamentally rule out the possibility that the observed performance differences are caused by random factors. It provides solid and quantitative statistical evidence for the core assertion that the proposed AC-MGME model exhibits strong performance in both generation accuracy and comprehensive performance.
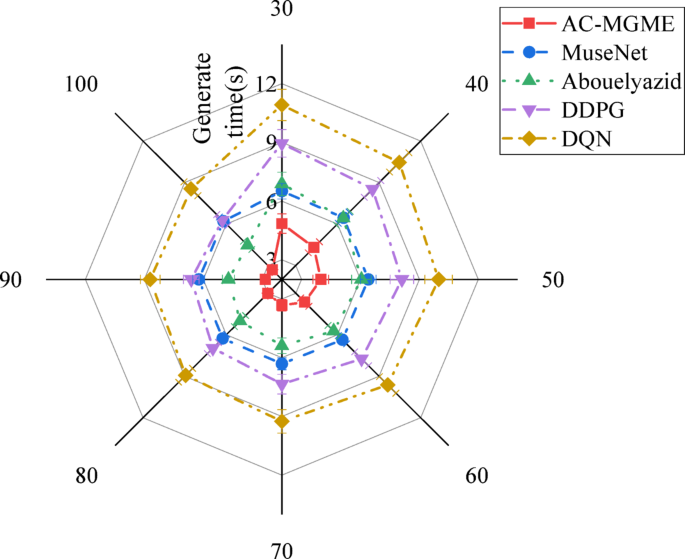
The comparison result chart of music melody generation time by each algorithm in LAKH MIDI v0.1 dataset.
Figure 6 illustrates how the developed AC-MGME model outperforms previous contrast models in terms of melody creation time efficiency. From the figure, the generation time of AC-MGME decreases steadily with the progress of training, reaching the lowest value among all models at the 100th epoch, which is only 2.69 s. In sharp contrast, the Transformer-based SOTA model MuseNet maintains an inference time of over 6.2 s, highlighting the limitations of large-scale models in real-time applications. Meanwhile, the efficiency of AC-MGME is also significantly superior to all other reinforcement learning-based comparison models.
To further verify the superiority of the AC-MGME model in computational efficiency from a statistical perspective, a two-sample t-test is similarly conducted on the melody generation time of each model at the final epoch (Epoch 100), as shown in Table 4.
In Table 4, in comparisons with all contrast models (including the heavyweight MuseNet and other reinforcement learning models), the p-values are all far less than 0.001. This extremely low p-value indicates that the shorter generation time exhibited by the AC-MGME model is not a random fluctuation in the experiment, but a significant advantage with high statistical significance. This finding provides decisive statistical evidence for the applicability of the model in real-time personalized music teaching applications that require rapid feedback.
To verify the generalization ability of the AC-MGME model in more complex musical environments, the final accuracy rates on the MuseScore dataset are compared, as shown in Fig. 7.
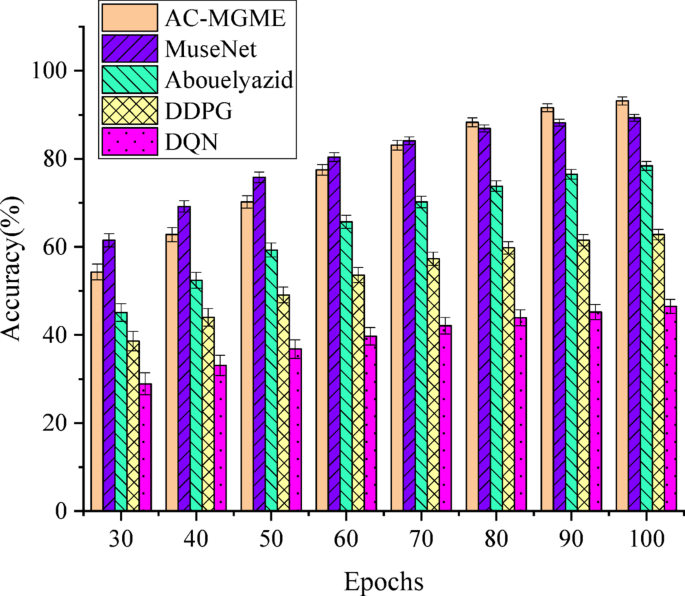
Accuracy results for music melody prediction by various algorithms in the MuseScore dataset.
In Fig. 7, due to the significantly greater complexity and diversity of the MuseScore dataset in terms of instrument types and musical styles compared to the LAKH dataset, there is a universal decline in the accuracy of all models, which precisely reflects the challenging nature of this testing task. Nevertheless, the AC-MGME model once again demonstrats its strong learning ability and robustness, topping the list with an accuracy rate of 90.15% in the final epoch. It is particularly noteworthy that, in the face of complex musical data, the advantages of AC-MGME over other reinforcement learning models (such as DDPG and DQN) are further amplified. It successfully surpasses the powerful SOTA model MuseNet in the later stages of training. This result strongly proves that the design of the AC-MGME model is not overfitted to a single type of piano music, but possesses the core ability to migrate and generalize to a wider and more diverse multi-instrument environment, laying a solid foundation for its application in real and variable music education scenarios.
To verify whether the generalization ability of the AC-MGME model across a wider range of instruments is statistically significant, a two-sample t-test is similarly conducted on the accuracy results of each model at the final epoch (Epoch 100) on the MuseScore dataset, as shown in Table 5.
In Table 5, the test results indicate that the performance advantage of the AC-MGME model is statistically significant. Even in comparison with its strongest competitor, MuseNet, its p-value (0.042) is below the 0.05 significance level. While the differences from models such as Abouelyazid (2023), DDPG, and DQN are even more pronounced (p < 0.001). This strongly proves that the leading position of this model on diverse, multi-instrument datasets is not accidental. More importantly, this conclusion fundamentally confirms the robustness and generality of the AC-MGME framework, indicating that it is not limited to the generation of single piano melodies but can effectively learn and adapt to the melodic characteristics of a wider range of instruments, thus having application potential in more diverse music education scenarios.
To evaluate the deployment potential of the model in real teaching scenarios, a dedicated test on inference performance and hardware resource consumption is conducted. The model’s performance is assessed not only on high-performance servers but also deploys on a typical low-power edge computing device (NVIDIA Jetson Nano) to simulate its operation on classroom tablets or dedicated teaching hardware. The comparison of inference performance and resource consumption of each model on high-performance GPUs and edge devices is shown in Fig. 8.
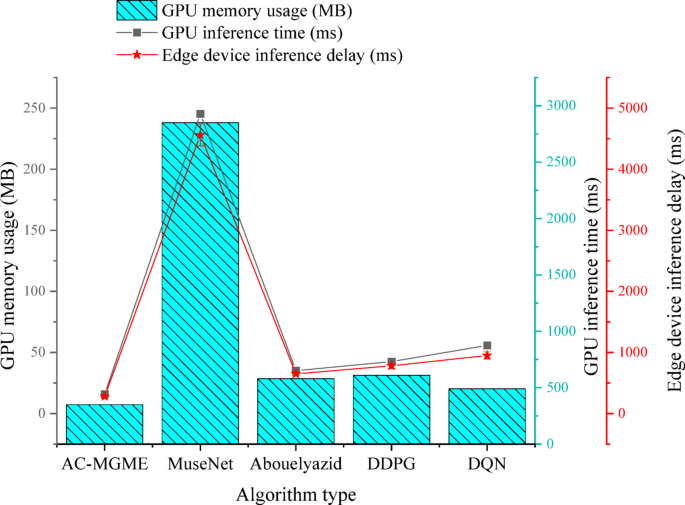
Comparison table of reasoning performance and resource occupation of each model on high-performance GPU and edge devices.
In Fig. 8, an analysis of the inference performance and resource consumption test reveals the significant advantages of the proposed AC-MGME model in practical deployment. In the high-performance GPU (NVIDIA Tesla V100) environment, AC-MGME not only demonstrated the fastest inference speed (15.8 milliseconds) but also had a GPU memory footprint (350 MB) far lower than all comparison models. Particularly when compared with the heavyweight Transformer model MuseNet (2850 MB), it highlighted the advantages of its lightweight architecture. More crucially, in the test on the low-power edge device (NVIDIA Jetson Nano) simulating real teaching scenarios, the average inference latency of AC-MGME was only 280.5 milliseconds, fully meeting the requirements of real-time interactive applications.
Two objective indicators, namely Pitch Distribution Entropy and Rhythmic Pattern Diversity, are further introduced to quantify the musical diversity and novelty of the generated melodies. This helps evaluate whether the model can generate non-monotonous and creative musical content. Among them, Pitch Distribution Entropy measures the richness of pitch usage in a melody. A higher entropy value indicates that the pitches used in the melody are more uneven and unpredictable, usually implying higher novelty. Rhythmic Pattern Diversity calculates the unique number of different rhythmic patterns (in the form of n-grams) in the melody. A higher value indicates richer variations in the rhythm of the melody. The comparison results and statistical analysis of the objective musicality indicators of the melodies generated by each model are shown in Table 6.
Table 6 reveals the in-depth characteristics of each model in terms of musical creativity, and its results provide more inspiring insights beyond the single accuracy indicator. As expected, MuseNet, as a large-scale generative model, obtains the highest scores in both Pitch Distribution Entropy and Rhythmic Pattern Diversity, and statistical tests shows that its leading advantage is significant (p < 0.05), which proves its strong ability in content generation and innovation. However, a more crucial finding is that the AC-MGME model proposed in this study not only demonstrates highly competitive diversity but also significantly outperforms all other reinforcement learning-based comparison models in both indicators (p < 0.01). This series of results accurately indicates that the AC-MGME model proposed in this paper does not pursue unconstrained and maximized novelty, but rather achieves much higher musical diversity and creativity than similar DRL models on the premise of ensuring the rationality of musical structures. This good balance between “controllability” and “creativity” is an important reason why it obtained high scores in subsequent subjective evaluations, especially in “teaching applicability”.
To evaluate the subjective artistic quality and educational value that cannot be captured by technical indicators, a double-blind perception study is conducted. 30 music major students and 10 senior music teachers with more than 5 years of teaching experience are invited as expert reviewers. The reviewers score the melody segments generated by each model anonymously on a 1–5 scale (higher scores indicate better performance) without knowing the source of the melodies. The user feedback results under the proposed model algorithm are further analyzed, including the scores (1–5 points) in three aspects: the use experience, the learning effect and the quality of the generated melody. The comparison results with traditional music teaching and learning are shown in Fig. 9.
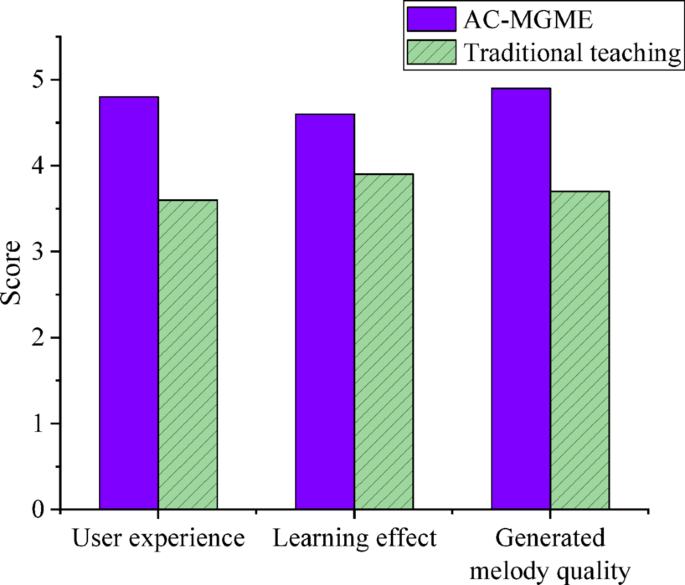
Comparison chart of user feedback results.
In Fig. 9, according to the feedback from users, the satisfaction of AC-MGME model is higher than that of traditional music teaching. Especially in the aspect of melody quality, AC-MGME gets a high evaluation of 4.9 points, which is significantly better than the traditional teaching of 3.7 points. In addition, AC-MGME also performs well in terms of experience and learning effect, with scores of 4.8 and 4.6 respectively, far exceeding the scores of 3.6 and 3.9 in traditional teaching. This shows that AC-MGME model not only improves the learning effect and student experience, but also provides higher quality results in melody creation.
The expert evaluation results of subjective quality of melodies generated by each model are shown in Table 7, and the statistical analysis results are shown in Table 8.
The results of Tables 7 and 8 show that, in the dimension of artistic innovation, MuseNet achieves the highest score with its strong generative capability, and its leading advantage is statistically significant (p = 0.008), which is completely consistent with the conclusion of the objective musicality indicators. However, in terms of melodic fluency, AC-MGME won with a slight but statistically significant advantage (p = 0.041), and expert comments generally considered its melodies to be “more in line with musical grammar and more natural to the ear”. The most crucial finding comes from the core dimension of teaching applicability, where the AC-MGME model obtained an overwhelming highest score (4.80), and its advantage over all models including MuseNet is highly statistically significant (p < 0.001). The participating teachers pointed out that the melodies generated by AC-MGME are not only pleasant to listen to, but more importantly, “contain clear phrase structures and targeted technical difficulties, making them very suitable as practice pieces or teaching examples for students”. This series of findings strongly proves that while pursuing technical excellence, this model more accurately meets the actual needs of music education, and can generate educational resources that combine artistic quality and practical value. This is a unique advantage that cannot be matched by models that simply pursue novelty or accuracy.
Discussion
The results of this study clearly demonstrate the comprehensive advantages of the AC-MGME model across multiple dimensions. In terms of objective performance, the model not only outperforms all comparison benchmarks, including state-of-the-art models, in accuracy and F1 score, but also confirms the reliability of this advantage through strict statistical significance tests (p < 0.05). More importantly, in the subjective quality evaluation, AC-MGME achieved an overwhelming highest score in “teaching applicability”, indicating that it does not simply pursue technical indicators, but precisely meets the core needs of music education—generating musical content that combines structural rationality, artistic fluency, and teaching practical value. In addition, through deployment tests on low-power edge devices, this study is the first to empirically prove that while ensuring high-quality generation, the model has great potential for efficient and low-latency deployment in real classroom environments, laying a solid foundation for its transition from theory to application.
This study indicates that the proposed AC-MGME model exhibits significant performance in terms of melody generation quality, learning effectiveness, and user experience. In terms of melody generation quality, the AC-MGME model scores 4.9/5, which is higher than that of traditional music teaching, demonstrating its strong ability to generate melodies with both artistic and technical merits. Meanwhile, AC-MGME also performs well in learning effectiveness, with a score of 4.6/5, which is higher than traditional teaching, proving its effectiveness in generating personalized learning paths and improving students’ skills. In terms of user experience, AC-MGME scores 4.8/5, also higher than traditional teaching (3.6/5), further verifying the advantages of the interactive and convenient teaching system based on DRL. This is consistent with the findings of Dadman et al. (2024)34 and Udekwe et al. (2024)35. Particularly in terms of generation time, AC-MGME only takes 2.69 s to generate a melody, while other models such as DQN require 8.54 s. AC-MGME not only improves the generation quality but also significantly enhances the generation efficiency. In addition, the model performs excellently in terms of generation quality (with an accuracy rate of 95.95% and an F1 score of 91.02% on the LAKH MIDI dataset), and its generation quality is higher than that of other tested models, supporting the feasibility of real-time applications. This is consistent with the research of Chen et al. (2024)36.
Therefore, the proposed model algorithm can efficiently generate melody and provide personalized learning experience. By dynamically adjusting the melody generation strategy, AC-MGME can optimize the generated content in real time according to students’ different needs and learning progress, which greatly improves the intelligence and personalization level of music education and provides valuable practical basis for the development of AI-driven music education tools in the future.
However, while affirming these achievements, people must carefully recognize the limitations and potential biases in the research. Firstly, in terms of datasets, although the introduction of the MuseScore dataset has greatly expanded the diversity of instruments, the content of both datasets still mainly focuses on Western tonal music. This may lead to poor performance of the model when generating non-Western music or modern atonal music, resulting in an “over-representation” bias in a broader cultural context. Secondly, the size of the user sample is also a limiting factor. Although the expert review panel composed of 40 music professionals has provided valuable in-depth insights, this scale is not sufficient to fully represent the diverse perspectives of global music educators and learners. Therefore, although the results of this study are robust within the test framework, caution is still needed when generalizing them to all music cultures and educational systems, and more localized verifications should be conducted.
Finally, the application of such AI technologies in the field of education will inevitably raise ethical issues that require serious attention. A core concern is the potential risk of abuse, particularly music plagiarism. The model may learn and reproduce copyrighted melody segments during training, thereby triggering intellectual property issues. To mitigate this risk, future system iterations must integrate plagiarism detection algorithms, for example, by comparing generated content with n-gram sequences in the training set, and design corresponding reward mechanisms to encourage originality. Another equally important ethical issue is the privacy and security of student data. While tracking and analyzing students’ practice data can enable personalized teaching, it also involves sensitive personal performance information. To address this, strict data management strategies must be adopted, including anonymizing and aggregating all data, ensuring system design complies with relevant regulations such as the General Data Protection Regulation (GDPR), and fully disclosing the content, purpose, and usage of data collection to students, parents, and teachers. These measures aim to build a trustworthy and responsible intelligent music education ecosystem.
