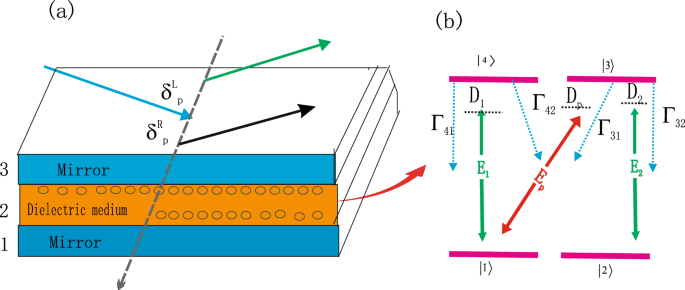
The two layers 1,3 in atomic model consists of a mirrors having dielectric function (epsilon _{1,3}) and layer 2 is four level dielectric medium having dielectric function (epsilon _{2}). The thickness of mirrors is represented by (d_{1,3}), whereas the intracavity atomic mediums have a thickness of (d_{2}) as demonstrated in Fig. 1a. The dielectric medium consists of a four-level configuration having probe field (E_{p}) and the control fields (E_{1,2}), as illustrated in Fig. 1b.
(a) A schematic arrangement features a coherent dielectric material positioned between two mirrors. Upon encountering the mirror surfaces, the incident light experiences a spin-dependent separation. (b) Shows a four-level atomic system influenced a probe beam and two control beams.
The unperturbed Hamiltonian is expressed as
$$begin{aligned} H_0= & sum ^{4}_{w=1}{hbar }omega _w left| wrightrangle leftlangle wright| end{aligned}$$
(1)
The modified Hamiltonian of the dielectric material is20,21.
$$begin{aligned} H_i= & -frac{hbar }{2}(R_1 e^{-iD_1t}left| 1rightrangle leftlangle 4right| +R_2 e^{-iD_2t}left| 2rightrangle leftlangle 3right| +R_{p} e^{-iD_{p}t}left| 1rightrangle leftlangle 3right| +H.C) end{aligned}$$
(2)
The density matrix method is employed to evaluate the coherence aspect of the probe field22.
$$begin{aligned} {dot{rho }}=&-frac{i}{hbar }[H_{I},rho ]-&sum frac{1}{2}Gamma _{ij}(U^{+}U^{-}rho +rho U^{+}U^{-}-2U^{-}rho U^{+}) end{aligned}$$
(3)
where (U^{+})( (U^{-})) denotes the creation (annihilation) operator associated with decay processes23 and indicates the decay rates between different atomic states. The steady-state coherence solution for the probe field is outlined below.
$$begin{aligned} {widetilde{rho }}_{13}=frac{2iR_{p}(4H_2H_3H_4-H_2R_1^2+H_3R_2^2)}{-R_1^4+(4H_1H_3-R_2^2)(4H_2H_4+R_2^2)+R_1^2(-4H_1H_2+4H_3H_4+2R_2^2)} end{aligned}$$
(4)
where (H_{1-4}) are given as:
$$begin{aligned} & H_1=iD_{p}-frac{G_{31}+G_{41}}{2} end{aligned}$$
(5)
$$begin{aligned} & H_2=i(D_1-D_{p}) end{aligned}$$
(6)
$$begin{aligned} & H_3=i(D_{p}-D_2)-frac{G_{32}+G_{42}+G_{31}+G_{41}}{2} end{aligned}$$
(7)
$$begin{aligned} & H_4=i(D_{p}-D_1-D_2)-frac{G_{32}+G_{42}}{2} end{aligned}$$
(8)
The susceptibility of the dielectric medium is (chi _{die}=frac{2N|varrho _{die}|^{2}}{epsilon _{0}hbar R_{p}}rho _{13}). Here N is atomic number density, (varrho _{die}) is dipole moments, ({widetilde{rho }}_{die}) is probe field coherence. The dielectric susceptibility is expressed as24
$$begin{aligned} chi _{die}=-frac{2Nvarrho ^2_{d}}{epsilon _0hbar R_{p}}{widetilde{rho }}_{13} end{aligned}$$
(9)
The permittivity of the dielectric medium is (epsilon _{2}=1+chi _{die}). The light beam approaches the cavity situated between the mirrors at an incident angle (theta _i) from the vacuum. The light can either reflect or transmit through the structure. As shown in Fig. 1a, The incoming beam’s left and right handed circular polarization components are separated spatially along a direction perpendicular to the plane of incidence. This lateral shift, referred to as the Photonic Spin hall Effect (PSHS), is an optical phenomenon influenced by polarization, resulting in photons with opposite helicities diverging because of the interplay between their spin and orbital angular momentum. This phenomenon can be viewed as the optical counterpart of the electron spin hall shift. For the three-layer setup under examination, the reflection coefficients are denoted as (r_p) for TM polarization and (r_s) for TE polarization in the following way25:
$$begin{aligned} & r_{p}=frac{r^{12}_{p}+r^{23}_{p}e^{2ik_{2z}d_2}}{1+r^{12}_{p}r^{23}_{p}e^{2ik_{2z}d_2}} end{aligned}$$
(10)
$$begin{aligned} & r_{s}=frac{r^{12}_{s}+r^{23}_{s}e^{2ik_{2z}d_2}}{1+r^{12}_{s}r^{23}_{s}e^{2ik_{2z}d_2}} end{aligned}$$
(11)
where (r^{12.23}_{p}) and (r^{12.23}_{s}) is the Fresnel’s reflection coefficient at the 1,2 and 3 interfaces are given by
$$begin{aligned} & r^{12}_{p}=frac{k_{1z}/epsilon _{1}-k_{2z}/epsilon _{2}}{k_{1z}/epsilon _{1}+k_{2z}/epsilon _{2}} end{aligned}$$
(12)
$$begin{aligned} & r^{23}_{p}=frac{k_{2z}/epsilon _{2}-k_{3z}/epsilon _{3}}{k_{2z}/epsilon _{2}+k_{3z}/epsilon _{3}} end{aligned}$$
(13)
$$begin{aligned} & r^{12}_{s}=frac{k_{1z}-k_{2z}}{k_{1z}+k_{2z}} end{aligned}$$
(14)
$$begin{aligned} & r^{23}_{s}=frac{k_{2z}-k_{3z}}{k_{2z}+k_{3z}} end{aligned}$$
(15)
where (k_{1z}=sqrt{k_{o}epsilon _{1}-k^{2}_{x}}), (k_{2z}=sqrt{k_{o}epsilon _{2}-k^{2}_{x}}) and (k_{3z}=sqrt{k_{o}epsilon _{3}-k^{2}_{x}}) is the wave vector within the respective layers and (k_{x}=sqrt{epsilon _{1}}k_{o} sintheta _{i}). Where (k_{o}=2pi /lambda) denotes wave vector.
As shown in Eqs. (10) and (11), the reflection coefficients depend on the dielectric medium’s permittivity, denoted as (epsilon _{2}), which can be actively modified by changing (chi _{die}). This variation results in a tunable Photonic Spin hall shift (PSHS) for incident light. Once the dielectric susceptibility is known, the PSHS can be calculated using the Fresnel reflection coefficients. The transverse spin shift, represented by (delta ^{L}{p}) and (delta ^{R}{p}), is defined based on the reflection coefficients associated with the three layers 1,2 and 3 are26.
$$begin{aligned} delta ^{L,R}_{p}=pm frac{k_{1}omega ^{2}_{o}Re[1+frac{r_{s}}{r_{p}}]cottheta _i}{k^{2}_{1}omega ^{2}_{o}+|frac{partial lnr_{p}}{partial theta _{i}}|^{2}+|(1+frac{r_{s}}{r_{p}})cottheta _i|^{2}} end{aligned}$$
(16)
Here (k_{1}=sqrt{epsilon _{1}}k_{0}) and (omega ^{2}_{o}) is radius of the incident beam’s waist.
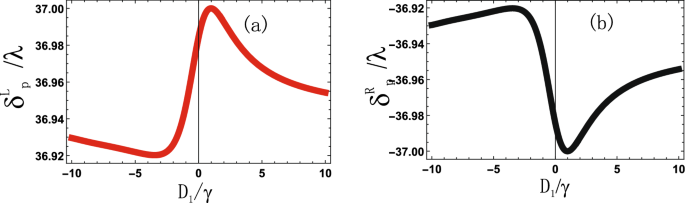
Spin hall shift (delta ^{L,R}_{p}) against control field detuning (D_{1}/gamma), (D_{2}=20gamma), (D_{p}=0gamma), (|R_1|=4gamma), (|R_2|=5gamma), (phi _1=pi /6), (phi _2=pi /2), (theta _i=pi /6), (Gamma _{31,32,41,42}=2gamma).
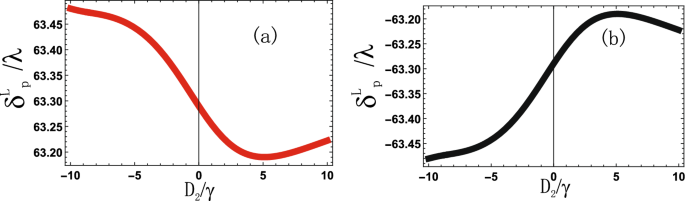
Spin hall shift (delta ^{L,R}_{p}) against control field detuning (D_{2}/gamma), (D_{1}=10gamma), (D_{p}=0gamma), (|R_1|=40gamma), (|R_2|=50gamma), (theta _i=pi /4), (phi _1=pi /6), (phi _2=pi /2), (Gamma _{31,32,41,42}=2gamma).
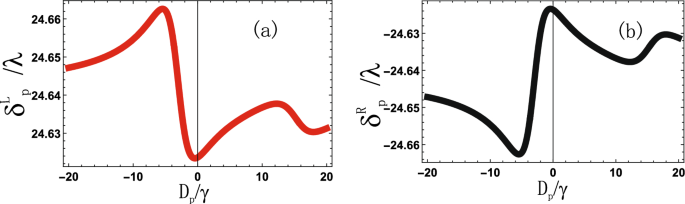
Spin hall shift (delta ^{L,R}_{p}) against probe field detuning (D_{p}/gamma), (D_{1}=20gamma), (D_{2}=10gamma), (|R_1|=10gamma), (|R_2|=15gamma), (theta _i=pi /6), (phi _1=pi /6), (phi _2=pi /2), (Gamma _{31,32,41,42}=2gamma).
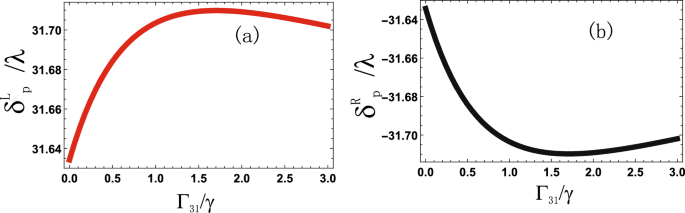
Spin hall shift (delta ^{L,R}_{p}) versus decay rate (Gamma _{31}/gamma), (D_{1,2}=10gamma), (D_{p}=0gamma), (|R_1|=2gamma), (|R_2|=4gamma), (phi _1=pi /6), (phi _2=pi), (theta _i=pi /4), (Gamma _{31,32,41,42}=2gamma).
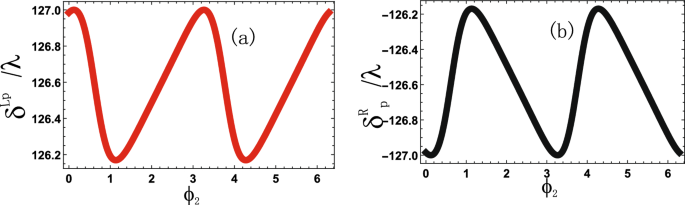
Spin Hall shift (delta ^{L,R}_{p}) versus control field phase (phi _2), (D_{p}=0gamma), (D_{1,2}=10gamma), (|R_1|=2gamma), (|R_2|=5gamma), (theta _i=pi /4), (phi _1=pi), (Gamma _{31,32,41,42}=2gamma).
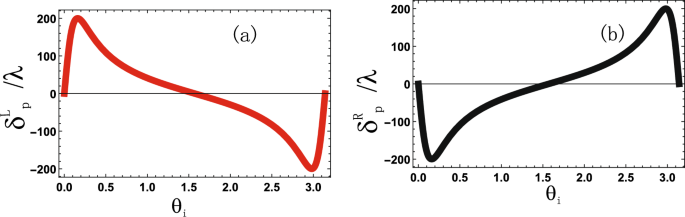
Spin hall shift (delta ^{L,R}_{p}) versus incidence angle (theta _i), (D_{p}=0gamma), (D_{1,2}=10gamma), (|R_1|=2gamma), (|R_2|=5gamma), (phi _1=pi), (phi _2=pi /2), (Gamma _{31,32,41,42}=2gamma).
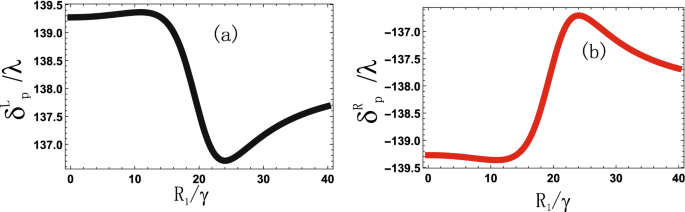
Spin hall shift (delta ^{L,R}_{p}) versus Rabi frequency (|R_1|/gamma), (D_{1}=20gamma), (D_{2}=10gamma), (D_{p}=0gamma), (|R_2|=15gamma), (theta _i=pi /3), (phi _1=pi /6), (phi _2=pi /2), (Gamma _{31,32,41,42}=2gamma).
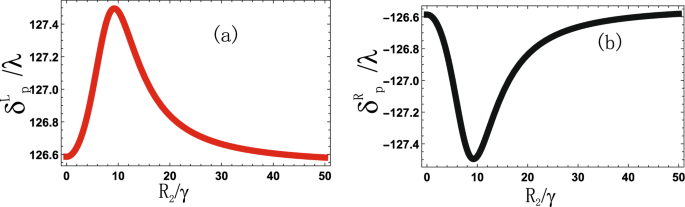
Spin hall shift (delta ^{L,R}_{p}) versus Rabi frequency (|R_2|/gamma), (D_{1,2}=10gamma), (D_{p}=0gamma), (|Omega _1|=2gamma), (theta _i=pi /3), (phi _1=pi /6), (phi _2=pi), (Gamma _{31,32,41,42}=2gamma).