Decentralized queue control with delay shifting in edge-IoT using reinforcement learning

Analytical modelling of the edge-IoT environment as a single-channel queueing system with controlled shift in distributions

In modern edge-oriented IoT environments, there is an increasing need for adaptive load regulation that considers constraints related to latency, energy consumption, and traffic class. This is particularly relevant for systems such as URLLC or mMTC, where response speed or transmission stability is critically important. Under such conditions, the problem of formal control over waiting time and queue length becomes pressing, without disrupting the overall flow structure. One of the key solutions involves introducing a shift parameter into the arrival and service distributions. For this purpose, let us consider single-channel queueing systems of the A/B/1 type in Kendall’s classification, where the symbols A and B denote the probability distributions of inter-arrival and service intervals respectively, and 1 indicates the number of service channels. The single-channel model is the most appropriate abstraction of an edge node. It reflects the hardware constraints of NB-IoT, LoRa, or BLE devices, which process requests sequentially rather than in parallel. Moreover, this model preserves the mathematical clarity of the analytical apparatus, particularly when using the spectral method³¹ for the Lindley equation³².

In A/B/1 queueing systems, the probability density functions (alpha left( t right)) and (beta left( t right)), corresponding to the distributions of inter-arrival times and service durations, respectively, are defined as time-shifted functions (tau), where (tau>0) is a controllable parameter characterising the minimum delay in the system

Here, (tilde {alpha }left( t right)) and (tilde {beta }left( t right)) represent the original (non-shifted) density functions of inter-arrival and service intervals, respectively. The introduction of the shift (tau) enables continuous adjustment of the expected values of the corresponding stochastic variables without altering their functional form. As a result, a controlled reduction in the coefficient of variation occurs, which is one of the main factors influencing the mean waiting time. Consequently, the parameter (tau) becomes a controllable variable that can be used to shape delays as an optimisation tool, for instance, to balance between QoS classes or minimise buffer overflow. Henceforth, it is assumed that the base densities (tilde {alpha }left( t right)) and (tilde {beta }left( t right)) belong to the class of functions that admit Laplace transformation. This is a critical requirement for applying the spectral method, which serves as the principal analytical tool used to derive the numerical-analytical characteristics of queue waiting time. As a result of introducing the controllable shift (tau) into the density functions (1), not only the expected values of the corresponding intervals are altered, but also the shape of the system’s overall variation profile is affected. In particular, increasing the mean values of the intervals while keeping the variance fixed leads to a monotonic decrease in the coefficients of variation, which has a decisive impact on queue characteristics. Since the mean waiting time in a G/G/1 system is directly proportional to the squares of the coefficients of variation of inter-arrival and service intervals, managing the shift opens the way to analytically controlled delay optimisation.

From a mathematical standpoint, a system with a regulated shift does not preserve Markovian properties, and its dynamics are described within the general G/G/1 class. In this class, the arrival and service flows may follow arbitrary structures, provided they admit a Laplace transform. To describe the distribution law of the queue waiting time, the Lindley integral equation is used in the following interpretation:

where (Wleft( x right)) is the distribution function of the queue waiting time, and (Fleft( {{v_xi }} right)) is the distribution function of the stochastic variable (rho =beta – alpha), which describes the difference between the service time (beta) and the inter-arrival interval (alpha) of two successive requests. The variable ({v_rho }) in this context is the integration variable that spans all possible values of (rho), i.e., all scenarios of relative positioning of arrival and service completion events. If ({v_rho }>0), the current request is forced to wait; if ({v_rho } leqslant 0), the service begins immediately. The controllable shift parameter (tau), introduced at the level of the distributions (alpha left( t right)) and (beta left( t right)), indirectly shapes the behaviour of the function (Fleft( {{v_rho }} right)), and thus governs the entire dynamics of request accumulation in the system.

To obtain an analytical solution to the Lindley Eq. (2) under arbitrary (non-Markovian) arrival and service distributions, it is appropriate to apply the spectral method³². This approach is widely used in the analysis of queueing systems, as well as in applied problems of mathematical physics and signal processing. In our model, this method preserves analytical controllability even in the absence of simplifying assumptions about the form of the densities. The core idea of the method is to transition into the Laplace transform domain, where the densities (alpha left( t right)) and (beta left( t right)) are represented as functions ({{rm A}^ * }left( p right)) and ({{rm B}^ * }left( p right)). This transition allows the integral Eq. (2) to be rewritten in the form of an algebraic relation:

where (p in {text{F}}) is the complex Laplace transform parameter, and (aleft( p right)), (bleft( p right)) are analytical functions (typically polynomials) that approximate the integral structure in rational form. Such a transformation enables the analysis of the system’s spectral structure, in particular the identification of its zeros and poles, which directly influence the temporal characteristics of the service process and determine the asymptotic behaviour of the waiting time.

For the subsequent analysis, we select two of the most representative distributions that combine analytical transparency with practical relevance for IoT edge subsystems – the exponential and the second-order Erlang distributions. Their selection is motivated by the fact that these distributions, on the one hand, possess closed-form Laplace transforms, and on the other hand, allow for the modelling of both reactive and multi-phase behaviour of service or arrival processes.

The exponential distribution serves as a fundamental model for memoryless stochastic events, such as spontaneous request generation by sensors or short computational tasks. Its shifted distribution function is given in

where (lambda) denotes the intensity of the exponential process. This distribution is characterised by a zero coefficient of variation, which makes it convenient for analytical anchoring and spectral interpretation of systems with constant load.

The Erlang distribution of order two, in turn, enables the modelling of structured, staged processes, particularly in cases where a request undergoes several stages of preliminary processing (filtering, authorisation, encryption). Its distribution function with adjustable shift (tau) is given in

where (mu) denotes the intensity parameter of each phase. Unlike the exponential distribution, this one exhibits a lower coefficient of variation, which allows for more precise control over load fluctuations and more efficient management of waiting times in the system.

Both distributions form a unified parametric axis, enabling a smooth transition from a fully random (exponential) to a sequential-phase (Erlang) mode without losing analytical controllability. This makes it possible, within a single spectral scheme, to model a wide range of edge scenarios () from lightweight requests with immediate service to complex transactions with sequential processing.

Within the described analytical framework, we consider queueing systems in which interarrival and service intervals are modelled by continuous stochastic variables with shifted distribution functions. Specifically, let us assume that the system dynamics are defined by two functions of the form ({F^{left( i right)}}left( t right)=left{ begin{gathered} {{tilde {F}}^{left( i right)}}left( {t – tau } right)forall t geqslant tau , hfill \ 0forall 0 leqslant t leqslant tau , hfill \ end{gathered} right.), where ({tilde {F}^{left( 1 right)}}left( t right)) and ({tilde {F}^{left( 2 right)}}left( t right)) denote the base (unshifted) distributions for arrivals and service, respectively. This formalisation generalises the previously considered exponential and Erlang cases, allowing a more abstract representation of systems with controllable delay. Interpretatively, this means that each process in the system initiates no earlier than after a fixed time interval (tau), reflecting hardware, protocol, or energy constraints typical of real-time edge nodes. Such a shift enables the reproduction of internal buffering, adaptive delays, and minimum activity intervals without disrupting the overall structure of the model. Importantly, the shifted distributions retain all key properties of classical queueing models that underpin spectral and Laplace-based methods.

After formalising the shifted form of the distribution functions (4), (5) and analysing their properties in the time domain, a natural step is to transition to the spectral representation, which is implemented via the Laplace transform. In the classical formulation, it is defined as

where (fleft( t right)) denotes the probability density function of the corresponding random variable. This transition to the complex domain enables the replacement of integral operators with algebraic ones and reveals the structure of functional relationships between model components in the form of products, quotients, and poles.

In the case of time-shifted functions (in particular, (fleft( {t – tau } right)), which equals zero for (left[ {0,tau } right))), the standard shift property ({text{L}}left[ {fleft( {t – tau } right)} right]={F^ * }left( p right)exp left( { – tau p} right)) is used, allowing the effect of controllable delay to be easily incorporated into the spectral image. This enables the previous relation (3) to be rewritten in the following form

where exponential factors associated with the shift parameter (tau) mutually cancel. As a result, the structural form of the spectral expression remains unchanged, which is a significant advantage: the shifted model does not require additional adjustment in the Laplace transform domain. This makes it possible to directly apply the spectral decomposition technique developed for classical systems, without any loss of generality or need to renormalise components.

Within the formulated model, we consider a queueing system in which both arrivals and service are described by two-phase Erlang densities with a symmetric delay structure. This approach reflects practical scenarios in which both incoming requests and their processing consist of sequential stages with a guaranteed minimum activation time, such as authentication and confirmation procedures. In the analytical representation, these densities take the form:

where (varphi ,phi>0) are the intensities of the phase components. Both densities are shifted to the right by (tau), ensuring consistency with the previously introduced logic of controllable delay.

After transitioning to the spectral domain, the corresponding Laplace transforms take the form:

where the factors (exp left( { – tau p} right)) arise as a consequence of the shift in the time domain. Since the exponential components in both transforms are synchronised, they cancel each other out within the product structure that appears in the spectral relation. After algebraic manipulation, we obtain:

where the coefficients ({k_0}), ({k_1}), ({k_2})​ depend solely on the model parameters and define the numerator as a third-degree polynomial. The pole structure of the fraction (10) is fully determined: singularities at the points (p=varphi) and (p=phi) define the dominant frequency behaviour of the system and determine the positions of the spectral peaks. This spectral localisation subsequently enables a precise analysis of the asymptotic characteristics of the waiting time.

Summarising the results of the spectral representation, we construct the Laplace transform of the waiting time function based on the rational structure of the fraction derived earlier. In the model with two-phase Erlang density distributions for arrivals and service, the corresponding transform ({W^ * }left( p right)) is given by

where ({Omega _+}left( p right)) is the regular part of the spectrum, and ({p_1}), ({p_2}) are the real positive roots of the denominator of the spectral decomposition, associated with the frequency characteristics of the system. Their presence determines the asymptotic behaviour of the waiting time function, including the dominant decay rates of the queue.

To complete the spectral construction, we refine the structure of the functions (aleft( p right)) and (bleft( p right)), which appear in relation (10) and define the spectral decomposition in the frequency domain:

where ({p_3}) is the pole of the function (bleft( p right)), located to the right on the complex axis and is the reciprocal of the characteristic time parameter of intensity (varphi). The rational form of both functions enables the efficient application of inverse transform methods and analytical approximation techniques.

The mean waiting time ({rm E}left[ W right]) is determined using the standard operator approach to the derivative of the spectral transform (11), or equivalently, through the analysis of partial fraction decomposition. We obtain:

which clearly illustrates the dependence of delay on the location of poles in the spectrum. According to formula (13), the value of ({rm E}left[ W right]) decreases with increasing ({p_1}), ({p_2})​, which, in turn, depend on the distribution parameters (primarily the mean intervals and coefficients of variation). Therefore, controlling these quantities opens the way to analytically formalised optimisation of delays in the system.

To proceed with the comparative analysis, we consider the generalised metric characteristics of the arrival and service flows. These quantities allow spectral results to be interpreted in terms of temporal scales and the dispersion properties of the system.

For the arrival flow, the corresponding values are calculated as:

where ({rm E}left[ {{T_varphi }} right]) is the mean interarrival time and ({c_varphi }) is the coefficient of variation, reflecting the degree of instability in the incoming traffic. Similarly, for the service flow we obtain:

In both cases, the coefficient of variation is a decreasing function of (tau), which confirms the earlier statement: increasing the shift stabilises the process by reducing relative dispersion and smoothing stochastic fluctuations.

In contrast to standard Erlang distributions without shift, where the coefficient of variation equals ({1 mathord{left/ {vphantom {1 {sqrt 2 }}} right. kern-0pt} {sqrt 2 }}), in the proposed model it is further reduced due to the presence of an unavailability phase. Consequently, both coefficients satisfy the inequality (0<{c_varphi },{c_phi }<0.5), indicating that the model belongs to the class of systems with limited variability, where the influence of random factors on the waiting time is significantly diminished. This creates the preconditions for predictable queue behaviour and effective real-time quality of service management.

Finally, let us consider the limiting case of the model with Erlang densities – Its transition to the exponential distribution with the same shift parameter (tau). This model corresponds to the classical M/M/1 system with activation delay, allowing an assessment of the impact of distribution order on the behaviour of the waiting time. In this case, the arrival and service densities take the form:

In contrast to the two-phase Erlang structure, this configuration exhibits memoryless behaviour with the highest possible variability (coefficient of variation (c=1)). In such a setup, the mean waiting time is determined by the classical formula for the M/M/1 model:

which, despite the presence of the shift (tau), retains its form due to the cancellation of exponential factors in the spectral domain, as demonstrated earlier.

The Laplace transforms of the densities (16) take the form:

and the product ({{rm A}^ * }left( { – p} right){{rm B}^ * }left( p right)) results in a rational fraction that describes the spectral structure of the model:

Unlike the previously considered cases, expression (19) has two simple poles, and the structure of the numerator is linear in (p), which simplifies inversion and facilitates the interpretation of queue dynamics. In this way, the shifted model remains fully compatible with the classical M/M/1 theory, while introducing a crucial element, controlled service unavailability over the interval (left[ {0,tau } right)), which is essential in realistic IoT scenarios.

In contrast to existing approaches that address task placement or energy-aware scheduling without formally modelling the internal queue structure, the proposed model introduces a parametrically controlled delay shift within a G/G/1 framework, enabling analytical control over key QoS metrics. For example, the study³³ formulates a stochastic game for distributed task coordination among UAVs, but does not explicitly model queue dynamics or device activation delay. Similarly³⁴, applies a vacation queue model to optimise application placement, yet its optimisation process is based on empirical heuristics and lacks an analytical linkage between service parameters and latency characteristics. The work³⁵ focuses on energy-efficient scheduling, but does not formalise the queue as a controllable element within the service process. The proposed model, by contrast, incorporates analytically derived expressions for mean waiting time (formula (13)) and coefficients of variation (formulas (14) and (15)), where the shift parameter (denoted (theta)) directly affects both temporal stability and service variability. The Laplace-domain representation (formulas (10) and (11)) enables spectral analysis of system behaviour under arbitrary input distributions. Furthermore, the shifted Erlang distributions defined in formula (8) allow precise modelling of activation delays typical for edge nodes. As a result, the proposed framework offers a mathematically grounded foundation for reinforcement learning that is explicitly sensitive to queue dynamics, structurally induced service delays, and decentralised real-time optimisation.

Intelligent control of the shift parameter in a queueing model for Edge-IoT environments using reinforcement learning

After formalising the analytical queueing model with a controllable shift, it is justified to proceed to the description of the mechanism for its intelligent control. The shift (tau), previously interpreted as a parameter defining the phase of system unavailability prior to processing, is hereinafter considered a controllable variable dynamically adjusted by the RL agent in response to the current system state. This is particularly relevant in edge-IoT environments, where load characteristics fluctuate unpredictably and the need to adapt to resource and timing constraints is critical.

The problem of optimal selection (tau) in this context is formalised as a Markov Decision Process (MDP), within which the RL agent observes the variation of queue parameters, selects actions from the set of admissible shifts, and receives a reward for reducing delay and improving system stability.

The state space (s) is defined by the key features of the current service configuration (S=leftlangle {q,rho ,{c_{ef}}} rightrangle), where (q) denotes the queue length, (rho ={varphi mathord{left/ {vphantom {varphi phi }} right. kern-0pt} phi }) represents the load intensity, and ({c_{ef}}) is the effective coefficient of variation. The latter can be specified as the average value between ({c_varphi }) and ({c_phi }), calculated according to formulas (14) and (15), which already incorporate the impact of the shift (tau) on the variability of incoming flows.

The action space ({rm T}) is a finite set of permitted shift values available for the agent to choose from: ({rm T}=left{ {{tau _1},{tau _2}, ldots ,{tau _n}, ldots ,{tau _N}} right}), ({tau _n} in left[ {0,{tau _{hbox{max} }}} right]). The boundaries of this set are determined by hardware, protocol, or energy constraints of edge devices, while its discrete nature allows for controlled complexity of the learning algorithms.

The reward function (Rleft( {s,{tau _n}} right)) integrates two key aspects of service performance: the average waiting time and the balance between the variability of service and arrivals. In its simplest form, it is expressed as

where ({rm E}left[ {Wleft( {{tau _n}} right)} right]) is defined by the spectral formula (13), which depends on the poles ({p_1}) and ({p_2}), indirectly influenced by the choice of shift (see expressions (10), (19)); (left| {{c_varphi } – {c_phi }} right|) serves as an indicator of variability imbalance; ({q mathord{left/ {vphantom {q {{q_{hbox{max} }}}}} right. kern-0pt} {{q_{hbox{max} }}}}) is the normalised queue length, directly reflecting the level of request accumulation; ({q_{hbox{max} }}) denotes the maximum permissible queue length; and the term (hbox{max} left( {0,rho – 1} right)) penalises situations where the arrival intensity exceeds the system’s computational capacity. The coefficients ({kappa _1},{kappa _2},{kappa _3} in {{mathbb{R}}^+}) define the relative importance of each criterion, taking into account architectural and service-level priorities.

The probabilistic transition function (Pleft( {s^{prime}left| {s,{tau _n}} right.} right)), which describes the change of state resulting from performing action ({tau _n} in {rm T}) in state (s in S), is empirically defined in most practical cases. The RL agent does not possess complete knowledge of the model; instead, it learns the queue dynamics through experience-based learning algorithms (off-policy).

The objective of the RL agent is to approximate the optimal policy ({pi ^ * }=arg mathop {hbox{max} }limits_{pi } {rm E}left[ {sumnolimits_{{t=0}}^{infty } {{gamma ^t}Rleft( {{s_t},{n_t}} right)} } right]), where (gamma in left( {0,1} right]) is the discount factor that determines the long-term significance of decisions.

The RL approach serves as a superstructure over the analytical framework outlined in subsection 2.1. It does not alter the structure of the Lindley equation or the spectrum (see expressions (3), (10), (19)), but rather uses them as a foundation for dynamic learning. Crucially, the RL agent operates not at the level of modifying the mathematical model itself, but at the level of managing its parameters, thus, enabling the system to adapt to load fluctuations and instability in incoming flows without sacrificing analytical predictability.

Function (20) formalises shift management (tau) as a MDP, in which the RL agent, interacting with the analytically grounded queuing system (see expressions (13)–(15)), develops a policy for dynamic action selection. However, in a practical edge-IoT environment, additional factors (such as buffer limitations, request losses, traffic class, and node energy capacity) play a decisive role alongside stability and service speed. Therefore, it is reasonable to introduce an extended reward function that complements function (20) with terms accounting for these application-specific requirements:

where (L={{{N_{drop}}} mathord{left/ {vphantom {{{N_{drop}}} {{N_{arrive}}}}} right. kern-0pt} {{N_{arrive}}}}) is the empirically estimated ratio of lost requests to total arrivals, (L in left[ {0,1} right]); ({L_{hbox{max} }}) is the permissible loss threshold defined by the QoS profile; (Eleft( {{tau _n},{c_{ef}}} right)) is the expected energy consumption, modelled in simplified linear form

where ({e_0},{e_1},{e_2} in {{mathbb{R}}^+}) are the parameters of the node’s energy profile corresponding to background consumption, delay cost, and processing of variable input flows; ({E_{hbox{max} }}) is the available energy consumption limit; and ({kappa _4},{kappa _5} in {{mathbb{R}}^+}) are the weighting coefficients. Each term in function (21) represents a measurable or predictable quantity calculated at the decision-making moment, ensuring a fully formalised agent policy without the need for heuristic tuning.

The extension of function (20) to the form (21) requires the construction of an agent-based architecture capable of making decisions regarding the value of the shift parameter (tau), based on observations of queue state, load characteristics, variability, losses, and energy consumption. Given that such key components of the reward as average waiting time and coefficients of variation are determined analytically (see expressions (13)–(15)), the RL agent does not approximate the service model, but rather operates as a strategic superstructure over an already adapted system.

The agent’s input is defined as a state vector (s=left( {q,rho ,{c_{ef}},L,E} right)), (s in S), where all variables are either available during execution (e.g. (q,rho)), (rho)) or computed using the mathematical framework defined in subsection 2.1. At the same time, reward components dependent on the selected action (in particular, ({rm E}left[ {Wleft( {{tau _n}} right)} right])) are not included in the state, as they are computed post hoc, after the action has been applied. As before, the RL agent’s action space is defined by the set of admissible shift values ({rm T}=left{ {{tau _i}} right}), (i=overline {{1,N}}). The discreteness of this set enables the use of tabular methods for policy learning. For such configurations, it is appropriate to apply the Q-learning algorithm, which updates the estimated utility of selecting ({tau _n} in {rm T}) in state s according to the rule:

where.(eta in left( {0,1} right]). is the learning rate, (left( {s,{tau _n}} right)) and (left( {s^{prime},{{tau ^{prime}}_n}} right)) denote the current and next states of the system, respectively; (Rleft( {s,{tau _n}} right)) is the reward function of the form (20) or (21), computed analytically based on the parameter ({tau _n}) and the observed state (s)s.

In cases where the dimensionality of the state space increases (for instance, due to the inclusion of additional QoS labels or changes in flow distributions), and the action set becomes broader, the RL agent can be implemented as a neural approximation of the Q-function, i.e. as a DQN. In this case, function (23) is modelled by a neural network with parameters (theta), which are updated by minimising the squared error between current and target estimates:

where ({theta ^ – }) denotes the parameters of the target network, updated with a delay. The DQN variant is appropriate in contexts where the management of (tau) is performed centrally using edge servers or gateway devices capable of real-time learning.

Thus, the optimal policy of the RL agent is defined as:

or, in the case of DQN:

The architecture generalised by expressions (23)–(26) implements a fully functional approach to system behaviour management without altering its internal structure. The RL agent, operating as a superstructure over the analytical core (13)–(15), performs adaptation to current load conditions, energy constraints, and service priorities (depending on the selected function (20) or (21)). This enables QoS-resilient, resource-aware control in practical edge-IoT scenarios, particularly in environments such as LoRaWAN, NB-IoT, or Smart Building Monitoring.

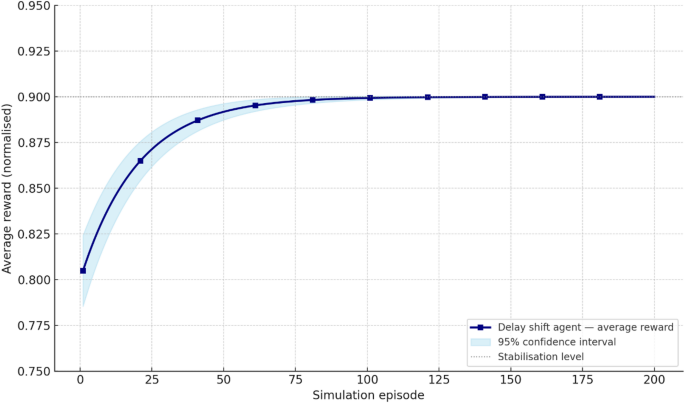
The construction of an effective policy for managing the shift parameter (tau) requires training the RL agent in a controlled environment that simultaneously reflects the analytical structure of the queuing model (see subsection 2.1) and allows flexible modelling of dynamic service conditions, losses, and energy consumption. Such simulation is a key instrument for validating the effectiveness of the chosen RL agent architecture and the reward function of the form (20), (21).

The simulator implements the integration of two components: the analytical core, which provides the computation of metrics (17)–(19), and the dynamic module, which updates the queue, overall costs, and energy expenditure. The current system state at step t is represented as ({s_t}=left( {{q_t},{rho _t},c_{{ef}}^{{left( t right)}},{L_t},{E_t}} right)). The RL agent selects an action ({tau _n} in {rm T}), corresponding to shift (tau _{n}^{{left( t right)}}), and the system transitions to a new state.

Within each simulation step of duration (Delta), the shift phase (tau _{n}^{{left( t right)}}) is implemented as a service delay. During this interval, arrivals continue, while processing is suspended. The new queue state is modelled according to the scheme:

where (Uleft( {tau _{n}^{{left( t right)}}} right)) is the number of new requests arriving during the shift, and (Dleft( {tau _{n}^{{left( t right)}}} right)) is the number of requests the system manages to process after the shift ends. The latter is computed as (Dleft( {tau _{n}^{{left( t right)}}} right)=hbox{min} left( {{q_t},phi left( {Delta – tau _{n}^{{left( t right)}}} right)} right)), which accounts for both queue limitations and the remaining service time. Losses are defined as the proportion of requests dropped due to buffer overflow: ({L_t}={{{N_{drop}}left( t right)} mathord{left/ {vphantom {{{N_{drop}}left( t right)} {Uleft( {tau _{n}^{{left( t right)}}} right)}}} right. kern-0pt} {Uleft( {tau _{n}^{{left( t right)}}} right)}}), and energy consumption is modelled as a linear function of the shift and flow variability: ({E_t}={e_0}+{e_1}tau _{n}^{{left( t right)}}+{e_2}c_{{ef}}^{{left( t right)}}). 

It is reasonable to train the RL agent under variable load conditions by following one of four typical scenarios:

• stationary (with constant (varphi), (phi));

• peak (with impulse load patterns);

• quasi-periodic (representing daily cycles in sensor networks);

• energy-constrained (with a variable energy budget).

To quantitatively assess the effectiveness of the strategy (pi left( s right)), the following metrics are accumulated:

where ({N_{rm T}}) denotes the number of iterations (simulation steps) during which the RL agent performs actions and the corresponding metric values are recorded.

The final stage of training the RL agent responsible for managing the shift parameter (tau) is the interpretation of the resulting policy (pi left( s right)) in terms of its stability, sensitivity to environmental changes, and generalisability beyond training scenarios. All actions of the RL agent are constrained within the discrete space ({rm T}), which ensures the preservation of the system’s spectral stability, particularly the invariance of the admissible pole placement in expression (10). The training procedure is formalised to ensure that the resulting policy (pi left( s right)) consistently reduces the average waiting time ({rm E}left[ W right]) while maintaining controlled losses ({rm E}left[ L right]) and balanced energy consumption ({rm E}left[ E right]). The sensitivity of the policy (pi left( s right)) to parametric changes was analysed through planned variation of (leftlangle {varphi ,{q_{hbox{max} }},{E_{hbox{max} }}} rightrangle) and the weighting coefficients ({kappa _i}).

To contextualise the proposed approach within the broader landscape of queueing and scheduling strategies for edge-IoT systems with strict QoS constraints, a comparative overview of relevant mathematical models is presented in the unnumbered table below. This summary outlines the structural and functional characteristics of classical stochastic queueing frameworks, threshold-based and protocol-imposed policies, task offloading schemes, and learning-driven delay management strategies. The models are compared in terms of their ability to regulate delay shifts, adapt to dynamic load conditions, and provide real-time responsiveness under decentralised operation. The final entry in the table summarises the distinctive contribution of this work, which formally integrates parameterised service delay control with reinforcement learning logic for locally autonomous decision-making.

Summary of Mathematical Models Considered in the Study.