Ventilator-free days (VFDs) introduced by Bernard et al. (1994) [1] have been commonly used as the primary endpoint in clinical care trials. The number of VFDs is defined as the number of days alive and free of mechanical ventilation during the measurement period. In the case of 28-day period, a patient is given a value of 0 if the patient dies on or before day 28 or is still on mechanical ventilator on day 28 [2]. Hence, VFDs combine mortality and duration of mechanical ventilation into a single measure.
Despite the composite nature, VFDs are often reported as a continuous or count variable with no distinction between a zero score from a patient who dies and a zero score from a patient who is alive but still on ventilator. VFDs are then analyzed by a t-test, the Wilcoxon rank-sum test, Poisson regression, or negative binomial regression to assess treatment efficacy. Excessive zeros from patients who die are likely to violate the distributional assumption for the t-test. When there are a substantial number of ties due to excessive zeros, the normal approximation to the null probability distribution of the rank-sum becomes questionable. Excessive zeros causing over-dispersion also invalidate analysis based on the Poisson or negative binomial distribution. Interpreting treatment effects from any of these tests that do not account for excessive zeros from mortality can lead to misleading conclusions. Several trials have reported that VFDs can lead to false conclusions that an intervention reduces both mortality and duration on mechanical ventilator when in fact the intervention affect only ventilator duration rather than mortality [3, 4].
Although both outcomes are significant, mortality is generally considered more consequential than prolonged mechanical ventilation. Assigning equal weights for death and prolonged mechanical ventilation may not reflect patient, family, clinician, or social values and beliefs [5]. Novack et al. (2020) [6] proposed a hierarchical outcome through modification of VFDs by treating death as a worse outcome than prolonged ventilation. Following Finkelstein and Schoenfeld (1999) [7], each patient is compared to every other patient in the trial and assigned a score (win = +1; lose = −1; tie = 0) for each pairwise comparison. Scores from all pairwise comparisons are summed for each patient and compared between two trial arms using the Wilcoxon rank-sum test. However, statistically significant results from the win-lose-tie approach cannot inform investigators as to the magnitude, nature, and direction of the intervention effects on mortality and duration of mechanical ventilation. Novack and colleagues suggested reporting mortality and ventilator-free days among survivors separately by treatment group along with the probability that an individual randomly selected from the study population will have a superior outcome if assigned to a given treatment arm.
Yehya et al. (2019) [4] considered mortality and achieving unassisted breathing as competing events and applied the Fine-Gray sub-distribution hazard model to assess the relative effect of an intervention on time to achieve unassisted breathing, accounting for the occurrence of death as a competing risk. Competing risks arise in clinical research when there are a number of potential failure events and the occurrence of one event prevents the occurrence of other events. While competing risk regression allows researchers and clinicians to account for the competing nature of death, Schoenfeld (2006) [8] advocated that endpoints such as 28-day or 60-day hospital mortality should be compared mainly during hospitalization using binary analysis methods such as (chi ^{2}) tests or logistic regression. He argued that survival methods such as Cox proportional hazards regression or competing risk regression are not appropriate because prolonged survival in patients who die during their hospitalization does not benefit the patients and, therefore, should not be measured in trials involving critically ill patients.
Verghis et al. (2023) [2] considered VFDs as zero-inflated count data and suggested modeling them using hurdle (or two-part) models [9] or zero-inflated models [10]. In a hurdle model, zeros from patients who die or patients alive but still on mechanical ventilator and non-zeros from patients alive and free of mechanical ventilation are analyzed separately. Logistic regression can be used to model the probability of having non-zero ventilator-free days in the first part and conditional on being non-zero, a truncated Poisson or negative binomial regression can be used to model the number of ventilator-free days among survivors achieving unassisted breathing in the second part. In a zero-inflated model, zeros are modeled as a mixture of structural (or true) zeros from patients who die and random (or sampling) zeros from patients alive but still on mechanical ventilator under the assumption that structural zeros are latent and not directly observable. Logistic regression can be applied to estimate the probability that an observed zero is a structural zero while a Poisson or negative binomial regression can be applied to model the number of ventilator-free days among patients not classified as structural zeros. Nevertheless, in the context of ventilator-free days, structural zeros due to death are observed rather than latent as its timing is known. Failing to explicitly model the source of these zeros either by treating zeros due to death as latent (as in zero-inflated models) or by assuming that all zeros, whether structural or random, come from a single generating process (as in hurdle models) can obscure important distinctions in treatment effects and lead to biased or misleading conclusions.
As VFDs combine mortality and duration of mechanical ventilation into a single measure, we propose a two-part model in which mortality is modeled in the first part and conditional on survival, the number of ventilator-free days is modeled in the second part. This approach aligns more closely with clinical interpretation of VFDs and avoids conflating deaths with poor but surviving outcomes from patients who survive but remian on a ventilator for the entire period. An indicator of death or survival is incorporated into the outcome variable VFDs to facilitate the proposed two-part modeling. Unlike the hurdle or zero-inflated model, the proposed two-part model not only provides a more comprehensive assessment of intervention effects on mortality and duration of mechanical ventilation but also helps investigators determine the magnitude and direction of intervention effects on mortality and duration of mechanical ventilation. To account for the cluster randomized cross-over design of the clinical trial that motivated this paper, each part of the two-part model also includes a random cluster effect that is assumed to be either shared, to account for a common latent cluster-specific quantity or trait that affects both the likelihood of mortality and duration of mechanical ventilation, or independent across the two parts. We conduct a simulation study to evaluate type I error rates and power of the different methods to detect an overall intervention effect. We illustrate the two-part model using data from the Pragmatic Airway Resuscitation Trial (PART) [11], a cluster randomized cross-over clinical trial to compare two airway management strategies for patients with out-of-hospital cardiac arrest.
PART trial
The PART trial was designed to compare the effectiveness of initial endotracheal intubation and laryngeal tube insertion on 72-hour survival in adults with out-of-hospital cardiopulmonary arrest (OHCA) [12]. More than 350,000 cardiac arrests occur outside of the hospital each year in the United States according to the American Heart Association. Endotracheal intubation is commonly performed by emergency medical services (EMS) professionals in which an endotracheal tube is inserted into the trachea to create an airway during cardiopulmonary resuscitation. Alternatively a laryngeal tube can be inserted into the pharynx and above the vocal cords. The PART trial included 27 EMS agencies from the Birmingham (Alabama), Dallas-Fort Worth (Texas), Milwaukee (Wisconsin), Pittsburgh (Pennsylvania), and Portland (Oregon) communities of the Resuscitation Outcomes Consortium [11]. These 27 EMS agencies were grouped into 13 clusters. Patients with OHCA were assigned to either initial endotracheal intubation (ETI) or initial laryngeal tube (LT) insertion based on a cluster randomized cross-over design in which each EMS agency alternated between interventions at 3-5-month intervals. There were 2 time periods in 2 clusters, 3 time periods in 3 clusters, 4 time periods in 6 clusters, and 5 time periods in 2 clusters. Patients with OHCA in each cluster within the same period received the same intervention, and randomization determined the order of interventions within a cluster. Further details on the PART trial are given in Wang et al. (2018) [12] and Wang et al. (2022) [11].
In this secondary analysis of the PART trial, the ventilator-free day outcome was defined as the number of days during the first 30 rather than 28 days of hospitalization that the patient was alive and free of mechanical ventilation. A patient with OHCA was given a value of 0 if the patient died without achieving return of spontaneous circulation (ROSC), died after achieving ROSC on or before day 30, or was still on mechanical ventilator on day 30. ROSC was defined as the presence of palpable pulses on emergency department arrival. Patients discharged alive from the hospital prior to 30 days were assumed alive and not on mechanical ventilator on day 30.
Of 3,004 patients with OHCA enrolled from December 1, 2015, to November 4, 2017, 1505 (51.1%) patients were randomized to initial LT and 1499 patients were randomized to initial ETI. The median age (interquartile range) was 65 (53-76) years and 1829 (60.9%) patients were men. For details on characteristics of these 3,004 patients by interventions, see Table 1 in Wang et al. (2018) [12]. Ventilator-free days were available for 2,947 (98.1%) patients in this secondary analysis. Of the 2,947 patients, 1831 (62.1%) patients [947 (64.8%) initial ETI and 884 (59.5%) initial LT] died without achieving ROSC, 884 (30.0%) patients [423 (28.9%) initial ETI and 461 (31.0%) initial LT] died after achieving ROSC on or before day 30, and 232 (7.9%) patients [92 (6.3%) initial ETI and 140 (9.5%) initial LT] were alive on day 30.
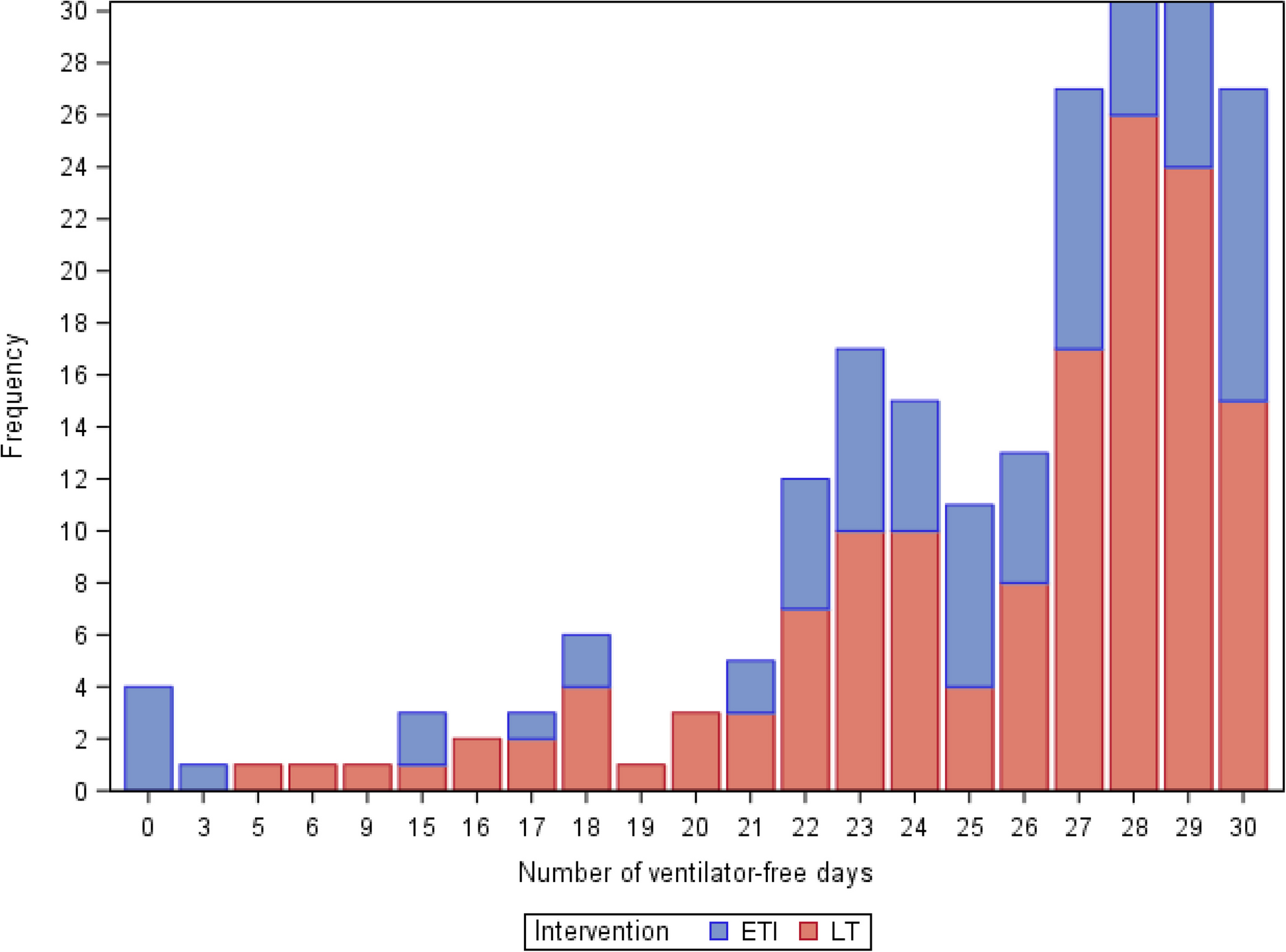
Of the 232 patients alive, 4 (1.7%) patients (4 initial ETI and 0 initial LT) were still on mechanical ventilator on day 30 whereas 189 (81.5%) patients [75 (39.7%) initial ETI and 114 (60.3%) initial LT] were discharged after 7 or less days of hospitalization. The mean ± SD number of ventilator-free days among survivors was 24.8 ± 6.7 in 92 patients initial ETI and 25.6± 4.6 in 140 patients initial LT. The histogram of the ventilator-free days in 232 patients alive is displayed in Fig. 1. From inspection of the figure, it appears that the distribution of the number of days alive and free of mechanical ventilation is towards the right side, leaving the left side heavily tailed. The binomial, Poisson, or negative binomial distribution is not likely to fit the observed left-skewed distribution of ventilator-free days well. Unlike the binomial distribution, the beta-binomial distribution allows the probability of success to vary from individual to individual, following a beta distribution. With two shape parameters from the beta distribution, the beta-binomial is flexible in fitting distributions that are flat, left-skewed, right-skewed, bell-shaped, U-shaped, or bimodal. The beta-binomial distribution can be used to fit the number of ventilator-free days in 232 patients alive.
Histogram of number of ventilator-free days in 232 patients achieving return of spontaneous circulation and alive on day 30
Two-part model
Let (Y_{ijk}) denote the number of ventilator-free days during the measurement period and (Z_{ijk}) be a response variable that can take on one of three possible values: 1 if the patient fails to achieve ROSC, 2 if the patient dies after ROSC, or 3 if the patient is alive for patient (k = 1, ldots , m) within period (j = 1, ldots , T) within cluster (i = 1, ldots , C). The probability function of (Y_{ijk}) is given by
$$begin{aligned} f(y_{ijk}) = left{ begin{array}{ll} P(Z_{ijk} = 1), & textrm{if} y_{ijk} = 0 , and , Z_{ijk} = 1;\ P(Z_{ijk} = 2), & textrm{if} y_{ijk} = 0 , and , Z_{ijk} = 2;\ (1 – P(Z_{ijk} = 1) – P(Z_{ijk} = 2)) f(y_{ijk} mid Z_{ijk} = 3), & textrm{if} y_{1ij} ge 0 , and , Z_{ijk} = 3. end{array} right. end{aligned}$$
Part 1: Let (P(Z_{ijk} = 1) = p_{1ijk}), (P(Z_{ijk} = 2) = p_{2ijk}), and (p_{3ijk} = 1 – p_{1ijk} – p_{2ijk}) that are modeled through multinomial logistic regression equations:
$$begin{aligned} textrm{log}left(frac{p_{1ijk}}{p_{3ijk}}right) = beta _{10} + beta _{11} x_{ijk} + delta _{1j} + u_{i} end{aligned}$$
(1)
and
$$begin{aligned} textrm{log}left(frac{p_{2ijk}}{p_{3ijk}}right) = beta _{20} + beta _{21} x_{ijk} + delta _{2j} + u_{i}, end{aligned}$$
(2)
where (x_{ijk}) indicates initial ETI or LT received by patient k within period j within cluster i, and (beta _{10}), (beta _{11}), (beta _{20}), and (beta _{21}) are unknown parameters. Fixed period effects are denoted by (delta _{1j}) and (delta _{2j}) with (delta _{11} = 0) and (delta _{21} = 0). Cluster-specific random effects are denoted by (u_{i}) that is assumed to follow a normal distribution with mean 0 and variance (sigma _{u}^{2}). A larger value of (u_{i}) implies that patients being treated in cluster i tend to have a higher probability of death without or after ROSC.
Part 2: Model the number of ventilator-free days among patients alive. Conditional on (Z_{ijk} = 3), (Y_{ijk}) is assumed to follow a binomial distribution, (Binomial (n, pi _{ijk})) with the probability of ventilator-free, (pi _{ijk}), assumed to follow a beta distribution, (Beta (a_{ijk}, b_{ijk})). Integrating with respect to (pi _{ijk}), we find that (y_{ijk}) follows a beta-binomial distribution with probability mass function given by
$$begin{aligned} f(y_{ijk} mid Z_{ijk} = 3) = left( begin{array}{c}{n}\ {y_{ijk}}end{array}right) frac{Gamma (a_{ijk} + b_{ijk})}{Gamma (a_{ijk})Gamma (b_{ijk})}frac{Gamma (a_{ijk} + y_{ijk})Gamma (b_{ijk} + n – y_{ijk})}{Gamma (a_{ijk} + b_{ijk} + n)}, end{aligned}$$
(3)
where (a_{ijk}> 0), (b_{ijk}> 0), and n is the length of the measurement period. For example, n is 30 in the PART trial.
The conditional mean and variance of (Y_{ijk}) are given respectively as
$$begin{aligned} E(Y_{ijk} mid Z_{ijk} = 3)= & ncdot frac{a_{ijk}}{a_{ijk} + b_{ijk}} nonumber \= & n mu _{ijk}. end{aligned}$$
(4)
and
$$begin{aligned} Var(Y_{ijk} mid Z_{ijk} = 3) = n mu _{ijk}(1 – mu _{ijk})left[1 + (n – 1)frac{phi _{ijk}}{1 + phi _{ijk}}right], end{aligned}$$
(5)
where (mu _{ijk} in (0, 1)) is the mean of the probability (pi _{ijk}) from the beta distribution and (phi _{ijk}= frac{1}{a_{ijk} + b_{ijk}}) is the dispersion parameter. We assume that the odds of a patient who fails to achieve ROSC or dies after ROSC (in Part 1) and number of days the patient is alive and free of mechanical ventilation (in Part 2) are correlated through a common random cluster effect (u_{i}). A logit link function is used to model (mu _{ijk}) as follows:
$$begin{aligned} textrm{log}left(frac{mu _{ijk}}{1 – mu _{ijk}}right) = gamma _{0} + gamma _{1} x_{ijk} + eta _{j} + gamma _{2}u_{i}, end{aligned}$$
(6)
where (x_{ijk}) indicates initial ETI or LT received by patient k within period j within cluster i; (gamma _{0}), (gamma _{1}), and (gamma _{2}) are unknown parameters; and (eta _{j}) are fixed period effects with (eta _{1} = 0). (gamma _{2}) is a real-valued association parameter that describes the dependency between Part 1 and Part 2, suggesting a common latent cluster-specific quantity attributing to a patient’s probabilities of both death and ventilator-free. If (gamma _{2}> 0), patients in a cluster with a higher latent cluster-specific quantity are more likely to be free of mechanical ventilation whereas if (gamma _{2} < 0), patients in a cluster with a higher latent cluster-specific quantity are less likely to be free of mechanical ventilation. If (gamma _{2} = 0), Part 1 and Part 2 are independent and can be modeled separately with each part having its own cluster-specific random effect. Note that the two-part model with a shared random cluster effect is a simplified version of the two-part model with correlated random cluster effects.
Let (d_{1ijk}) be 1 if (Z_{ijk} = 1) and 0 otherwise, and (d_{2ijk}) be 1 if (Z_{ijk} = 2) and 0 otherwise. Under the conditional independence assumption, the marginal likelihood for the kth patient within period j within cluster i is
$$begin{aligned} L_{ijk}(theta ) = int p_{1ijk}^{d_{1ijk}}p_{2ijk}^{d_{2ijk}}[(1- p_{1ijk}- p_{2ijk})f(y_{ijk} mid Z_{ijk}=3, u_{i})]^{(1 – d_{1ijk}- d_{2ijk})} g(u_{i}) , du_{i}, end{aligned}$$
(7)
where (theta = (beta _{10}, beta _{11}, beta _{20}, beta _{21}, gamma _{0}, gamma _{1}, gamma _{2}, delta _{1j}, delta _{2j}, eta _{j}, sigma _{u}^{2})), (p_{1ijk}) and (p_{2ijk}) are given in (1) and (2), (f(y_{ijk} mid Z_{ijk}=3, u_{i})) is given in (3), and (g(u_{i})) is the density function for (u_{i}). The likelihood to be maximized is
$$begin{aligned} L(theta ) = prod _{i=1}^{C}prod _{j=1}^{T}prod _{k=1}^{m} L_{ijk}(theta ). end{aligned}$$
(8)
The likelihood in (8) involves integrating a nonlinear function over the shared random effect given in (7). Quasi-Newton methods along with adaptive Gauss-Hermite quadrature to approximate the integral can be applied to find the maximum likelihood estimator for (theta = (beta _{10}, beta _{11}, beta _{20}, beta _{21}, gamma _{0}, gamma _{1}, gamma _{2}, delta _{1j}, delta _{2j}, eta _{j}, sigma _{u}^{2})). This approach can be implemented in statistical software packages such as R, SAS or Stata.
On a final note, there are three effects associated with the intervention in the two-part model. One is the intervention effect on odds of death without ROSC measured by (beta _{11}) in (1), another one is the intervention effect on odds of death after ROSC measured by (beta _{21}) in (2), and the last one is the intervention effect on odds of being ventilator-free measured by (gamma _{1}) in (6). The likelihood ratio test or the Wald test can be used to determine whether there is an overall intervention effect through testing the null hypothesis of (beta _{11} = beta _{21} = gamma _{1} = 0).