Stabilizing effect of amino acids on protein and colloidal dispersions

Second osmotic virial coefficient

A common way to evaluate the stability of a compound in a dispersion is through the equation of state (EOS)^8,9,31:

where Π is the osmotic pressure, ρ is the number density and kT is the product of the Boltzmann constant (k) and the temperature (T). In this equation, B is the virial coefficient, with the subscript numbers indicating the component of the dispersion—1 for the solvent, and 2 and 3 for the main and minor solute. Therefore, B₂₂ is the osmotic second virial coefficient that measures the self-interaction among the main solutes. When all virial coefficients have a value of 0, the EOS becomes equivalent to that for the ideal gas. A virial expansion is needed to represent realistic dispersions.

Origin of the energy landscape in the PMF of the nanoparticle

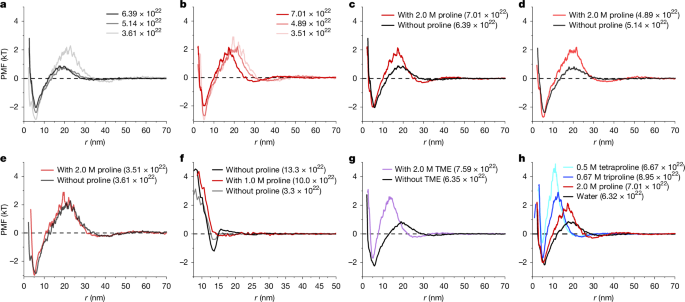
For nanoparticles, we observe a peak in the PMF at around twice the diameter D, and the height and position are concentration dependent. Given its range, this peak indicates that a longer-range attractive force is at play. The origin of the peak comes from the competition between the well-known plasmonic coupling between gold nanoparticles and a screened Coulomb repulsive force between the charged particles. The strong attractive well is due to ligand–ligand contact interactions. A sketch of all the interactions at play is shown in Supplementary Fig. 9. Previous calculations by our group have estimated the depth of the well for similar-sized nanoparticles (neglecting plasmons) to be of the same order of magnitude as that measured in this paper¹¹. This deep well should not be affected by the presence of AAs. However, at distances above the contact point, there is an attractive contribution to the potential due to electrostatic dipole–dipole couplings in the form of plasmon coupling.

Exclusion of other mechanisms

As directly demonstrated by SIC (Fig. 2b), we measure positive changes in ΔB₂₂ at AA concentrations as low as 10 mM, corresponding to a molar ratio of lysozyme to AA of about 1:7 (shown for glutamine in Supplementary Fig. 10, representative for all AAs). We performed a classical hydrotrope assay³², in which the solubility of a hydrophobic compound (fluorescein diacetate, FDA) in water is measured as a function of hydrotrope concentration. As shown in Supplementary Fig. 5, we did not find a threshold concentration for proline as the minimum hydrotrope concentration. Furthermore, we tested ΔB₂₂ dependence on the absolute concentration of the AA or on the stoichiometric ratio between the AA and the protein. We found that ΔB₂₂ depends only on the absolute AA concentration and not on that of the proteins (Supplementary Fig. 11).

Theoretical framework

For the simplicity of presentation, we discuss below the case of AAs interacting with proteins, but the model is general and is developed for small molecules interacting with nanoscale colloids in a dispersion. Consider a set of n colloidal particles with z attractive patches, with which they can interact with other identical colloidal particles. Given the coordination number z, we can think of this problem as that of colloids in a lattice with coordination given by z. We set the volume of a lattice point to be approximately the volume of the colloids a³, for simplicity. The coordination number depends on the number of patches and is an open variable, but it will generally be a number of order 10 or less (for example, the coordination number for a face centre cubic lattice would be 12, but it is 2 for divalent patchy particles). The coordination number sets the fictitious lattice on which we will work, but it is not important for the rest of our calculations, nor does it have further implications. The energy between two colloids is considered to have strong short-range repulsion (hard core), short-range attraction between patches (hydrophobic effect), screened long-range repulsion (electrostatic) and longer-range attraction from dipole–dipole interactions (Supplementary Fig. 9). This model is analogous to the DLVO theory. The increase in B₂₂ can be obtained by screening the short- or long-range attraction, which, in turn, increases the effect of repulsive forces. The latter, longer-range attractive term is important in the case of polarizable gold nanoparticles. In this case, the adsorption of zwitterionic AAs onto the ligand shell will screen NP–NP attractive dipole–dipole interactions, but leave the repulsion for the most part untouched, given that the excess AAs will be within the ligand shell because of hydrophobic attraction.

For simplicity, we will start with purely short-range interactions, which are applicable to most proteins. For this case, the free energy (per site) can be constructed directly from a mean-field (Bragg–Williams) approach to yield

where ϕ is the volume fraction of the colloids within the solvent. The interaction is completely captured by the incompatibility parameter χ (normally referred to in soft matter as the Flory χ parameter)

where the different ϵ values represent an effective interaction energy (per patch) of either colloid–colloid (CC), solvent–solvent (SS) or the cross-interaction colloid−solvent (CS). As can be seen from equation (4), increasing (or decreasing) the incompatibility parameter χ, which dictates the enthalpy of mixing, can be accomplished by increasing (decreasing) the strength of the interactions ϵ values, or by changing the effective coordination of the colloids z. We believe that the mechanism by which AAs modulate the colloid–colloid interaction is a competition-type of interaction, meaning AAs decrease z by blocking attractive patches and hydrating them. This is seen in the PMF of apoferritin (Fig. 1f), in which the short-range attractions disappear on increasing the concentration of AAs. The second virial coefficient can be extracted from the expansion of the free energy, and is written as

Note that in the absence of attractive interactions (that is, χ → 0), the excluded volume becomes the lattice site volume. More generally, we should evaluate the second virial as ({B}_{22}=-frac{1}{2}int ({{rm{e}}}^{-U/kT}-1){rm{d}}{bf{r}}), where U is the pair interaction potential. It is important to note that in the model we are studying, the attractive interaction parametrized by χ is assumed to be a contact interaction of very short range, that is, a contact interaction occurring only on contact with the particles, and this gives rise to the interacting part scaling with a³. This is a good approximation in the limit that the interactions are short ranged, which we believe applies to proteins under biological conditions. However, if long-range electrostatic repulsive or attractive interactions are present, we would need to add a constant to the virial potential and express it as

where ({Delta B}_{22}^{{rm{elec}}}=-frac{1}{2}{int }_{a}^{infty }({{rm{e}}}^{{-U}_{{rm{e}}{rm{l}}{rm{e}}{rm{c}}}/kT}-1){rm{d}}{bf{r}}). For a pure Coulomb potential, we find that ({Delta B}_{22}^{{rm{elec}}}) does not converge, but it does for a Debye–Yukawa potential, which is expected under the conditions typically encountered in colloidal solutions. As can be seen from equation (6), this generalized form of the second virial coefficient is similar to the original case where no electrostatic contributions were assumed. We need to rescale only the effective size of the colloid by the effective repulsive excluded volume and rescale the attractive part accordingly. Thus, for simplicity, we will assume from here on equation (6) without losing generality, with the understanding that a³ corresponds to an effective excluded volume and not just the steric contribution. As will be seen below, this rescaling does not affect any of our results.

Now we turn our attention to the effect of AAs or similar small molecules. We assume that AAs adsorb onto some patches of the proteins, which is in agreement with literature reports that have observed the adsorption (that is, weak interaction) of some AAs onto protein surfaces^33,34,35,36. The adsorption is transient, but it equilibrates rapidly because the barriers to adsorb and desorb are small, and the diffusion constant of the AAs is large compared with that of the proteins themselves^37,38. Thus, we can think of this system as consisting of an adsorption onto a surface with Nz adsorption sites, where N is the number of proteins and each has z patches to adsorb onto. We will assume, for simplicity, that one patch can only adsorb one AA or small molecule. This is not a strict condition and can be easily relaxed by assuming each patch has a given number of adsorption sites. We can model this adsorption process using the Langmuir adsorption isotherm, in which we can compute the fractional coverage (fraction of adsorbed sites) as

where c is the concentration of AAs and K is the equilibrium constant of binding between AAs and attractive patches. These quantities can be measured or computed.

The effective coordination is then given by z = z₀(1 − θ), with z₀ being the original number of patches in the absence of AAs. Finally, the second virial coefficient becomes

where F({ϵ}) is a function that depends only on the original interaction parameters and is independent of the concentration of AAs.

The second virial coefficient in the absence of AAs (when θ = 0) can be written as

and the change in the virial coefficient on addition of AAs is then simply given by

Inserting the expression of ({B}_{22}^{{rm{o}}}) in terms of F({ϵ}) in ΔB₂₂ from equation (9) and explicitly considering the fraction of sites, we find that the change of the second virial coefficient is an expression independent of the interaction energies:

This expression is insightful because it shows that the scale of change in the second virial is dictated by the difference between the maximum excluded volume the colloid can have given by a³ (stemming from purely repulsive interactions, steric + electrostatic, as discussed above), and the measured and actual excluded volume in the absence of AAs, that is, ({B}_{22}^{{rm{o}}}) that does include the effect from attractive patches. The change is regulated by the number of blocked attractive sites and patches given by the Langmuir expression, in which the equilibrium constant K can be extracted by fitting. It is important to mention that we are treating all patches equally. This condition can be relaxed (as shown below) and does not affect the results we are presenting. Furthermore, this relationship allows the quantification of the strength of the interaction that will lead to noticeable changes; these will happen when the product of K and c is in the range of 1.

We further introduce f_max, a small molecule-dependent parameter that captures the intrinsic affinity of a molecule to cover the surface of a particle. As shown in Fig. 2a,b, the plateau for proline-stabilized lysozyme is almost twice that of glycine-stabilized lysozyme. The assumption implicit in the Langmuir model that results in equation (11) is that the whole surface is made of identical patches and all small molecules will take ΔB₂₂ to the same plateau at infinite concentration. This is not observed experimentally. f_max is the maximum fraction of the surface that a small molecule can cover. In other words, it is the fraction of patches in the surface to which the small molecule can adsorb. Equation (11) becomes

It is important to note that we have made some approximations, namely, we have assumed that all the patches are equal and have the same interaction energy. This implies that we are not distinguishing the actual orientation of the bonds between colloids, nor the relative difference in interaction between different patches and the solvent. Although this is not true in general, we can think of the interacting patches that drive aggregation as a subset of patches and can lump the contributions of the other patches onto an effective interaction parameter that is not affected by the presence of the AAs. This can be calculated explicitly by considering, for example, two different subsets of patches. The total number of patches z = z₁ + z₂, and the respective interactions will be ({{epsilon }}_{{rm{SS}}},,{{epsilon }}_{{rm{CS}}}^{1},{{epsilon }}_{{rm{CS}}}^{2},{{epsilon }}_{{rm{CC}}}^{{rm{1,1}}},{{epsilon }}_{{rm{CC}}}^{{rm{2,2}}},{{epsilon }}_{{rm{CC}}}^{{rm{1,2}}}). Invoking the mean-field approximation as used above, we obtain the same free energy form with

where f₁ = z₁/z and f₂ = z₂/z, with the condition f₁ + f₂ = 1. Regrouping this equation, we can see that if, for example, patches of type 1 can be screened by the AAs, whereas patches of type 2 will not, then

where

The Δχ term does not change on adding AAs, so the aforementioned change in the second virial coefficient holds, even if the total χ parameter is negative from Δχ, in the approximation of χ₁ being much smaller than Δχ.

Cloud point determination

The critical temperatures (T_cr) and critical lysozyme concentrations (C_cr) were found by fitting the coexistence curves by the following equation (11):

where C_p is the protein concentration; β = 0.33 is the critical exponent; and α, T_cr and C_cr are the adjustable parameters³⁹.

A 20 mg ml⁻¹ lysozyme solution in 1× PBS was filtered through a 0.45-µm syringe filter and concentrated in Amicon tubes (10 kDa cut-off, Ultra-15) by centrifuging at 5,000 rpm at 20 °C for 50 min. Lysozyme concentration was measured by Implen NanoPhotometer (Implen) at 280 nm using an extinction coefficient of 2.72 mg⁻¹ ml cm⁻¹. The concentration of the lysozyme stock solution was adjusted to 200 mg ml⁻¹. The stock solutions of the AAs were prepared by dissolving the amino acid powder in water (Milli-Q) until a final volume of 1 ml was reached and adding 1 ml of 2 M NaCl solution in 2× PBS. The two-fold serial dilution of the stock solutions of AAs was done in 1 M NaCl solution in 1× PBS. Mixing of protein and amino acid solutions as well as transferring of the samples (100 µl) to capillaries (0.3 ml Crimp Neck Micro-Vial, 31.5 × 5.5 mm, clear glass, round bottom) were performed in ThermoMixer F1.5 Eppendorf at 42 °C. The blocks in a CrystalBreeder (Technobis Crystallization Systems) were kept at 42 °C for 10 min before the capillaries were placed into the instrument. The transmissivity was calibrated automatically after 5 min of temperature equilibration of the sample at 42 °C, followed by cooling down at a rate of 0.2 °C min⁻¹ under constant nitrogen flow to prevent protein oxidation. The cloud point temperature was registered at 70% transmissivity loss.

Detailed synthesis and characterization

Hen egg-white lysozyme (14.3 kDa, ≥95%) was purchased from Roche. All the AAs were purchased from Thermo Scientific in powder form. FUS-LCD was a gift from Prof. Dufresne¹⁵. BSA was purchased from Thermo Scientific. Ferritin and apoferritin were ordered from Sigma-Aldrich. Poly-proline peptides (tri- and tetra-proline) were purchased from Bachem Americas. 1,1,1-Tris(hydroxymethyl)ethane (TME, 97%) was purchased from ABCR Swiss. Plasmid DNA (4207 bp dsDNA, pIVEX1.3-CAT) was purchased from Biotechrabbit. The salts for the sodium phosphate buffer were also purchased from Sigma-Aldrich in powder form.

Synthesis of nanoparticles

HAuCl₄·3H₂O (789.3 mg), oleylamine (64 ml) and n-octane (80 ml) were mixed in a 500 ml three-necked round-bottom flask. The mixture was left stirring till the solid completely dissolved. The flask was connected to argon flow for 10 min followed by a quick injection of 16 ml of tert-butylamine-borane complex (351.3 mg) dissolved in oleylamine to induce the reduction reaction. The reaction was constantly stirred for 1 h and quenched with 240 ml of ethanol. Nanoparticles were precipitated with centrifugation. This was followed by sonication adding fresh dichloromethane and then ethanol several times and reprecipitated each time before adding fresh ethanol to remove organic residuals from reaction materials. Oleylamine (90 mg) functionalized nanoparticles was dissolved in 30 ml dichloromethane (dissolved with 34.86 mg of sodium mercapto-undecane sulphonate (MUS) and 31.23 μl of octane thiol). The ligand exchange was kept sealed and under stirring for 21 h. The nanoparticles after ligand exchange were sonicated and precipitated several times with fresh dichloromethane and acetone to remove organic residuals. Then pre-purified nanoparticles were dissolved in ultrapure water using Amicon 30 kDa MWCO filters for further purification to remove MUS. NMR of nanoparticles is presented in Supplementary Fig. 1 to show the quality of purification as well as the final composition of the two ligands functionalized on the nanoparticles.

Purification of ferritin based on sucrose density gradient ultracentrifugation

Ferritin, from equine spleen type I (Sigma-Aldrich, in saline solution), known to have a wide distribution of ferritin because of different iron loads, oligomerization or apoferritin impurities⁴⁰, was purified using preparative ultracentrifugation. Sucrose gradients in Mili-Q water (5–30 wt%) were prepared in six ultracentrifuge tubes (Ultra-Clear, 25 × 89 mm, SW28, Beckman Coulter, USA) by a Piston Gradient Fractionator (BioComp Instruments). Ferritin solution (400 µl) was loaded onto the gradient, followed by centrifuging (Optima XPN-80, Beckman Coulter) in a SW32 rotor, followed by centrifugation at 30,000 rpm at 20 °C for 2 h. Then three fractions were collected in a top-down manner (the liquid surface being 0 mm), at distances of 20–28 mm (fraction 1), 28–36 mm (fraction 2) and 36–46 mm (fraction 3). Each fraction was purified five times with 1× PBS in Amicon tubes (100 kDa cut-off, Ultra-15), at 4,000 rpm, 4 °C for 30 min. Quality of purification were characterized by analytical ultracentrifugation in sedimentation velocity (AUC-SV) (Supplementary Fig. 12). For AUC-SV, 380 µl of 1× PBS (reference) and 376 µl of the sample were loaded into 12 mm cells in an An60-Ti rotor and equilibrated at 20 °C in vacuum for 2 h, followed by velocity scans at 15,000 rpm with an absorbance profile collected at 280 nm. Data analysis was done using SEDFIT software⁴¹ with maximum entropy regularization at a confidence level of 0.68, final s-resolution of 500 in s-interval from 0 S to 250 S. For the cryo-EM measurement, fraction 2 was chosen due to its relatively monomeric distribution at around 60 S that is typical for ferritin⁴⁰ (Supplementary Fig. 12). Concentration of ferritin was measured by Implen NanoPhotometer (Implen) at 420 nm using an extinction coefficient⁴² of 10 mg⁻¹ ml cm⁻¹.

Cryogenic transmission microscopy

A total of 3.5 μl of dispersion was cast onto a previously glow-discharged quantifoil grid (Quantifoil R 1.2/1.3, 200 Mesh, Cu). The grid with solution was blotted with Whatman filter papers on both sides in a vitrobot (Vitrobot Mark IV) at 100% humidity and 22 °C, followed by immediate vitrification in liquid ethane. Imaging was performed at the Dubochet Center for Imaging (Lausanne) using a Titan Krios G4 microscope operating at 300 kV. Tilt series were recorded from −60° to 60° with two increments at a magnification of 33,000× (camera pixel size of 0.37 nm), a defocus of about 7 μm and a total dose of 120 e⁻¹ Å⁻². For data processing, pre-aligned .mrc files were compiled from Tomography v.5.16.0 (Thermo Fisher Scientific) and Camera Falcon 4i equipped with Selectris X energy filter (slit width 20 eV).

Generating PMF curves from cryo-ET tomograms

Details of this workflow were published in ref. ¹⁰. The contrast of the tomogram was inverted using ImageJ (NIH). High-contrast nanoparticles became white in the tomogram. Extra slices on the bottom and top of the tomograms, where there were no particles, were trimmed away to reduce the size of the tomogram. The tomogram was exported as a whole in the mrc file format and then imported into Imaris (Bitplane) for visualization and segmentation in *.ims format. The segmentation to detect particles was performed by following the steps of the built-in Surface detection function in Imaris, with seed growth selection turned on to dissect particles that are close to each other. The coordinates of the detected particles were exported to a text file and further processed for flatness and tilt correction. A rectangular box containing particles were cropped out and used for calculation of the radial distribution function. The particle coordinates are exported to the final text file that contains three columns; each row contains a 3D position (x, y, z) for a particle. It is read into the previously published Python program to calculate the radial distribution function. The PMF is found to be the logarithm of this function multiplied by thermal energy K_BT. Typical tomograms and their segmentation are shown in Supplementary Figs. 13–15.

Column grafting for SIC experiments

For this work, we adapted and optimized the experimental procedure for the custom-made column grafting with lysozyme and the protocol established in ref. ¹³ for our SIC experiments. For the grafting of the SIC column, a Tricorn 5/50 column (Cytiva, Column Volume of 1.178 ml) was manually grafted with lysozyme (Lys) using TOYOPEARL AF Formyl-650M chromatography particles, sodium cyanoborohydride, potassium phosphate and ethanolamine as a resin. The standard buffer used throughout the experiments was 50 mM sodium phosphate at pH ≈ 6.9, consisting of monobasic and dibasic sodium phosphate in MilliQ water.

All experiments were performed on SIC columns with a grafted surface coverage of lysozyme of around 45%. The column was packed under pressure with the following flow rates: 0.75 ml min⁻¹ for 15 min, then at 3 ml min⁻¹ at 15 min and again at 0.75 ml min⁻¹ for 30 min. The column was stored at 4 °C overnight and between experiment days.

SIC experiments

To prepare a chromatography column for a CIC experiment, Lys was manually grafted on the column, as outlined in the previous section, and for the optimized signal-to-noise ratio of the elution profile, we determined that the protein concentration should be around 20 mg ml⁻¹, which was injected in all SIC experiments in this work.

SIC experiments were conducted to probe the Lys self-interaction in different solution environments (buffer alone or in the presence of small molecules, such as AAs, poly-proline and TME at different concentrations dissolved in buffer) from which the respective values of B₂₂ were calculated. Before each measurement series, a column performance test was run with 20% acetone in Milli-Q water. For each run of the experiments, 50 µl of lysozyme at 20 mg ml⁻¹ was injected. Samples were injected after 10× column volume and with a constant flow rate of 0.75 ml min⁻¹ at room temperature. The AAs tested were proline, glycine, serine, threonine, asparagine and glutamine, and their concentration was varied between 5 mM and 1.2 M (considering their respective solubility limit). The upper range limit was set by the fact that towards the solubility limit of an added molecule (for example, amino acid, polyproline peptides, TME), the buffer solution becomes turbid, which very likely clogs and thus breaks the column. Therefore, to protect the grafted column, we set the upper limit to 1.2 M, a range well below the solubility limit of the studied AAs and small molecules.

Determination of B
₂₂ by SIC

In SIC experiments, we evaluate the interactions between the injected protein in the mobile phase and the immobilized protein grafted on the column in terms of the measured retention volume. To experimentally determine B₂₂, we first compute the retention factor k′ = (V₀ − V_R)/V₀, where V₀ is the retention volume of non-interacting species, which is calculated before each experiment with the column performance test using 20% acetone in MilliQ water and V_R is the volume required to elute the injected protein in the mobile phase through the grafted column. Then B₂₂ (mol ml g⁻²) can be computed as

where ({B}_{{rm{HS}}}=,2{rm{pi }}{r}^{3}/3{N}_{{rm{A}}}{M}^{2}) is the excluded volume or hard-sphere contribution of the two interacting proteins, assuming a spherical shape, s is the immobilization density, that is, the number of covalently immobilized protein molecules per unit area of the bare chromatography particles and Φ = A_sV₀ is the phase ratio (that is, the total surface available to the mobile phase protein). To calculate B_HS, we used the hydrodynamic radius r (1.89 ± 0.03 nm) and the average molecular weight M = 14,300 g mol⁻¹ of the self-interacting lysozyme¹⁷; N_A is Avogadro’s number. To exchange the units for B₂₂ (mol ml g⁻²), which is commonly used in SIC experiments, to one of the AUC experiments B₂₂ (m³) = B₂₂ (mol ml g⁻²)M₂/N_A10⁻⁶.

The assumption here is that we measure only two-body interactions, that is, one injected free protein interacts with only one immobilized protein molecule at a time. This constraint can be guaranteed by controlling the immobilized proteins grafted onto an effectively flat surface being the column. Another assumption is that the injected free Lys interacts only with one immobilized Lys grafted onto the column and not with each other. This can be verified by determining the variation for the calculated B₂₂ value measured at a concentration of 5–30 mg ml⁻¹ of the lysozyme. For the Lys–Lys self-interaction, the obtained B₂₂ value should remain constant. We determined this variation to be about 3.4 × 10⁻²⁶ m³ for Lys–Lys and considered this variation in our error analysis.

Sedimentation diffusion equilibrium analytical ultracentrifugation

In a typical SE-AUC experiment, a protein solution in phosphate buffer (pH 7, 50 mM) at a typical concentration of 10 mg ml⁻¹ was mixed with AAs. The final solutions were added into the AUC cells (3 mm pathlength). Gold nanoparticles were measured using capillary cells⁸. The sedimentation diffusion equilibria with a depleted meniscus at a proper angular velocity, 20 °C were reached typically after 24 h. The protein concentration gradient was obtained and converted into the EOS curve by the previously established methods⁹.

Intrinsic fluorescence measurements of lysozyme

All fluorescence measurements were performed with the CaryEclipse fluorometer (Agilent) using a 1.0-cm quartz cuvette. The fluorescence spectra of lysozyme (10 µM) with variable concentrations of proline (0−1 M), glycine (0–1 M), serine (0–1 M) and alanine (0–1 M) were measured at a constant temperature (25 °C). The volumes of the samples were adjusted to 1.5 ml with 50 mM sodium phosphate buffer, at pH = 6.9. The samples were excited at 290 nm, and the fluorescence was recorded from 310 nm to 420 nm with an em/ex slit of 5 nm and a scanning speed of 120 nm min⁻¹.

If it is assumed that there are similar and independent binding sites in the protein, the binding constant (K_D) and the number of binding sites (n) can be determined using the following equation^43,44:

where F₀ and F are the fluorescence intensities in the absence and presence of AAs, respectively. Q is the quencher concentration, for example, amino acid. k_D and n can be determined by the intercept and the slope of the linear regression of (log left(frac{{F}_{0}-F}{F}right)) compared with log(Q).

Dynamic light scattering

Lysozyme and BSA solutions, about 0.8 mg ml⁻¹, in phosphate buffer (pH 7, 50 mM) were filtered (0.22 µm) before DLS measurements using Nano ZS from Malvern. All DLS measurements were performed with three replicates.

Sedimentation velocity AUC study of insulin aggregates

Before AUC-SV experiments, insulin was dissolved in a glass vial containing saline (NaCl 0.9%) and in a glass vial containing saline (NaCl 0.9%) with 1 M proline, respectively. The two vials were subjected to mechanical mixing in identical conditions in a tilting shaker at the same time and for the same duration of 1 h. Clear saturated insulin solutions were obtained by brief low-speed centrifugation of the vials to remove large visible aggregates. AUC-SV measurements were performed immediately afterwards in a Beckman Coulter Optima XL-I analytical ultracentrifuge equipped with an AN-60 rotor. Two-sector cells with a titanium centrepiece (path length of 12 mm, Nanolytics) and sapphire windows were used. The AUC was stabilized at least 2 h before start. The experiments were conducted at 20 °C at 60,000 rpm, in absorbance mode with no delay set between scans. Sedfit (v.17.0) was used to fit the experimental data to obtain the distribution of sedimentation coefficients C(s), which was then displayed by GUSSI.

Cell culture

HeLa cells (CCL-2) were cultured in Dulbecco’s modified Eagle medium (high glucose, GlutaMAX supplement), supplemented with 10% foetal bovine serum and 1% penicillin–streptomycin. The cells were cultured at 37 °C, 5% CO₂.

Immunofluorescence microscopy

The HeLa cells were plated in an ibidi 8-well µ-Slide at a seeding density of 1.5 × 10⁴ cells ml⁻¹ 24 h before the experiment. The cell culture media were replaced with fresh cell culture media supplemented with 200 mM of proline and incubated at 37 °C, 5% CO₂ for 1.5 h. The cells were then incubated at 43 °C, 5% CO₂ for 30 min for the heat shock treatment and fixed with 4% formaldehyde phosphate-buffered saline (PBS) for 15 min. The fixed cells were then permeabilized with 0.25% Triton X−100 in PBS for 15 min and blocked with 20 mg ml⁻¹ bovine serum albumin in PBS. The cells were first incubated overnight at 4 °C with the primary antibody, mouse anti-G3BP mAb (1:300, Abcam) and then incubated for 45 min at room temperature with the secondary antibody Alexa Fluo 488 (AF488) goat-anti-mouse IgG (1:300, Abcam). Then cell nuclei were stained with 4′,6-diamidino-2-phenylindole (DAPI) (1:1000, Sigma-Aldrich) for 15 min at room temperature and F-actin was stained by Alexa Fluor 555 Phalloidin (1:500, Thermo Fischer) for 35 min at room temperature. The fixed cells were then imaged using the Leica SP8 inverted confocal microscope with a 63× oil-immersion objective (NA = 1.40, HC PL APO, Leica). All z-stack images were acquired with the same z-step size of 1 μm and the same pixel dwell time of 3.16 μs.

Pharmacokinetic study

For the pharmacokinetic study, 500 ng of insulin was dissolved in saline or with 1 M proline in saline. Each group consisted of 5 mice, which were administered the solution by subcutaneous injection. Simultaneously, 10 mg of glucose was administered intraperitoneally. Mouse plasma was collected at various time points, and insulin concentrations were measured at these different time points using ELISA kits. The pharmacokinetic parameters were fitted using a non-compartmental analysis of plasma data after extravascular input using the package PK-solver.

Animal care

All animal procedures were performed in compliance with protocols approved by the Animal Care and Use Committee of the Southern University of Science and Technology (resolution number: SUSTech-JY202407031). During all animal experiments, the Chinese law and the local Ethical Committee Quantita Protocol were followed.

Details on ELISA detection

The ELISA kit used for insulin detection was purchased from Solarbio (catalogue no. SEKH-0219). Thirty minutes before the experiment, the reagent kit was allowed to return to room temperature. Before starting, the enzyme-linked plate was soaked three times and patted dry. Standard and test samples (100 µl each) were added to the reaction wells. The plate was sealed and incubated with shaking at room temperature (25 ± 2 °C) for 120 min, then washed plate four times and patted dry. Biotinylated antibody working solution (100 µl) was added to the reaction wells. The plate was sealed and incubated with shaking at room temperature (25 ± 2 °C) for 60 min, then washed four times and patted dry. Enzyme conjugate working solution (100 µl) was added to the reaction wells. The plate was sealed and incubated with shaking at room temperature (25 ± 2 °C) for 30 min, then washed five times and patted dry. Chromogenic substrate (100 µl) was added to the reaction wells. The plate was sealed and the colour developed in the dark at room temperature (25 ± 2 °C) for 5–20 min. Stop solution (50 µl) was added and the OD value at a wavelength of 450 nm measured within 5 min using an ELISA reader.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.