Every survey finding published by Pew Research Center comes with a margin of sampling error.
In our charts, we sometimes illustrate the margin of error through error bars, which can also be called confidence intervals. Center researchers typically calculate margins of error using a 95% confidence level. But what do the error bars mean? How should they be interpreted?
Here are some answers to common questions that might help you better understand charts with error bars.
What do error bars indicate?
Error bars illustrate the margin of error for a survey estimate by showing how precise that estimate is. To explore this concept in more detail, let’s revisit a recent Center analysis examining public attitudes about abortion in all 50 states and the District of Columbia.
The analysis found that 62% of adults in Ohio say abortion should be legal in all or most cases. In the chart excerpt below, the error bars extending from either side of the plotted point show that the margin of error for this estimate is plus or minus 3 percentage points. Statistically, that means support for legal abortion in Ohio could plausibly fall somewhere between 65% (3 points higher than our estimate) to 59% (3 points lower). We can expect the true value of support for legal abortion in Ohio to fall somewhere within the range highlighted by the error bars.

Why are some error bars longer than others?
Error bars can also give a sense of the survey’s sample size – that is, the number of people we interviewed.
Generally speaking, the margin of error for a survey estimate is determined in large part by the sample size. Estimates based on large samples are more precise and have smaller margins of error; estimates based on smaller samples are less precise and have larger margins of error.
Thus, our estimates for a big state like Texas, where we surveyed thousands of respondents, are more precise and have fairly short error bars. In smaller states like Delaware, where we surveyed fewer people, our margin of error is larger, and so are the error bars.

How should readers interpret error bars for multiple survey estimates?
The main purpose of error bars is to show an individual estimate’s level of precision. But they can also tell you how two different estimates compare.
When the error bars for two estimates do not overlap at all, it means the two estimates are significantly different from each other, statistically speaking.
Comparing estimates from different states
Let’s go back to our example above, showing support for legal abortion in Texas and Delaware.
In Texas, 56% of adults support legal abortion, and the error bar shows that the true value could be as high as 59%.
In Delaware, 73% of adults favor legal abortion, and the error bar shows that the true value there could be as low as 66%, after accounting for the 7-point margin of error.
There is no overlap between the error bar for Texas (which maxes out at 59%) and Delaware (which bottoms out at 66%). So we can conclude that support for legal abortion is statistically lower in Texas than in Delaware.
Comparing estimates from the same state
Error bars can also help illustrate whether support for legal abortion is higher or lower than opposition within a single state.
Again, we know that 73% of people in Delaware support legal abortion and that the true value for this estimate, after factoring in the margin of error, could be as low as 66%.
In the same survey, 26% of Delaware residents told us they think abortion should be illegal in all or most cases. Once the margin of error for this estimate is taken into account, the true value of opposition to abortion in Delaware could be as high as 33%.
In the chart excerpt below, the error bar around support (shown in blue) doesn’t come close to overlapping with the error bar around opposition (shown in orange). So we can conclude that far more people in Delaware support legal abortion than oppose it.
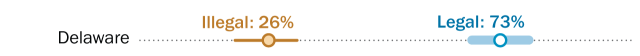
What does it mean when error bars overlap?
The picture becomes more complicated when error bars overlap. While overlapping error bars often indicate that two estimates are not significantly different from each other, statistically speaking, this is not always the case. Whether two estimates with overlapping error bars are significantly different depends on a variety of technical factors, and there is not a good rule of thumb for interpreting them that can be applied across the board.
When error bars overlap, these kinds of statistical comparisons require calculations that are difficult to depict in a chart. In these cases, it’s good practice to use caution in interpreting the differences as either significant or insignificant. When you see a chart with overlapping error bars in a report, the text will often include context and analysis to help interpret that chart.
Do error bars include all of the possible sources of error in opinion polls?
No. Error bars only illustrate sampling error. They show how far off an estimate might be from the true value because it’s based on interviews with a random sample of the population, rather than every single member of the population.
But there are other reasons a survey estimate can differ from the true value. For example, we know that some kinds of people are more likely than others to respond to surveys. If the people who respond have different views from the people who don’t respond, it can lead to nonresponse bias. Similarly, if some survey participants interpret a question differently than others, that can also introduce inaccuracies that are not reflected in error bars.
Unfortunately, these kinds of “nonsampling” errors are usually impossible to measure or calculate mathematically. As a result, error bars understate the true amount of error.
Related: When writing about survey data, 51% might not mean a ‘majority’