BPNN model results
The optimal number of neurons for the developed BPNN model was 50, the best training function was the Levenberg-Marquardt, and the best transfer function was Tan-sigmoidal. The learning rate and the momentum used for the BPNN model were 10− 4 and 0.9, respectively. Evaluation matrices for training, validating and testing phases were recorded during the running process of BPNN model, and the parameters that performed better on the basis of relation coefficient (R) and average absolute error (AAE) considered the models optimum parameters as:
$$:R=sqrt{frac{sum:_{i=1}^{n}{left({CA}_{pred,i}-{overline{CA}}_{act}right)}^{2}}{{left({CA}_{act,i}-{stackrel{-}{CA}}_{act}right)}^{2}}},$$
(16)
$$:AAE=frac{1}{n}left(sum:_{i=1}^{n}left|{CA}_{act,i}-{CA}_{pred,i}right|right)/left(frac{1}{n}sum:_{i=1}^{n}{CA}_{act,i}right),$$
(17)
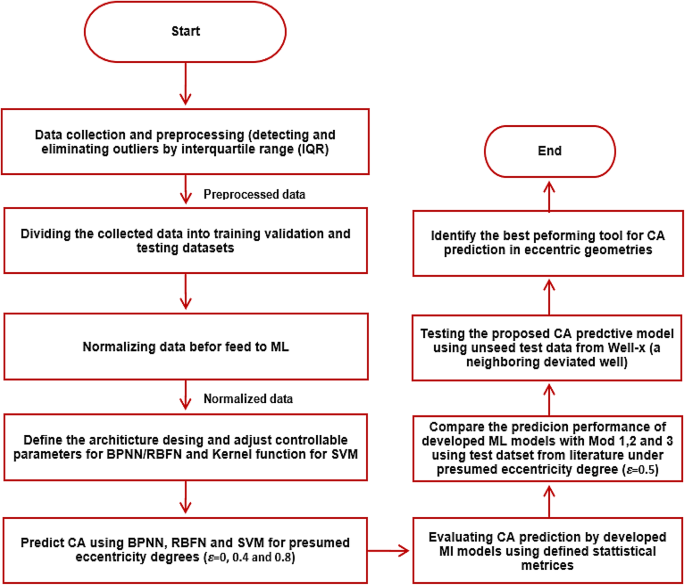
Figure 7 demonstrates the BPNN algorithm limited capability in predicting CA, with R-values of 0.893, 0.817, and 0.853 and AAE-values of 5.2, 5.4 and 6.3 for = 0, 0.4 and 0.8, respectively. These results indicate that the developed BPNN model struggles to accurately predict CA, as evidenced by poor statistical performance metrics.
BPNN regression plots for: (a) ε=0; (b) ε=0.4; (c) ε=0.8 BPNN modelling.
SVM model results
The SVM method has been used to predict CA. The results of the training show that the SVM performance model is acceptable regarding an overall R-values of (0.87, 0.86 and 0.83) and AAE-values of 4, 7 and 2 for = 0, 0.4 and 0.8, respectively. Table 5 summarizes the training results obtained for implementing SVM for the different eccentricity models, aiming for the best training correlation coefficients. Accordingly, the quadratic SVM shows the lowest AAE among SVM algorithms. Figure 8 shows the regression plots for the implemented SVM algorithms. Additionally, Fig. 9 describes the SVM response plots of predicted ad actual CA for every training record number. SVM regression results show that the best correlation coefficients are related to medium Gaussian quadratic and cubic SVM algorithms.
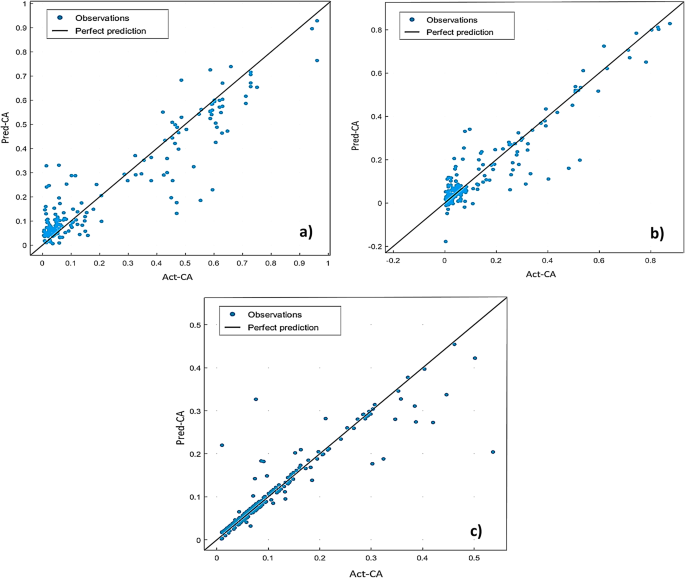
Quadratic SVM regression plots for: (a) ε=0; (b) ε=0.4; (c) ε=0.8 SVM modelling.
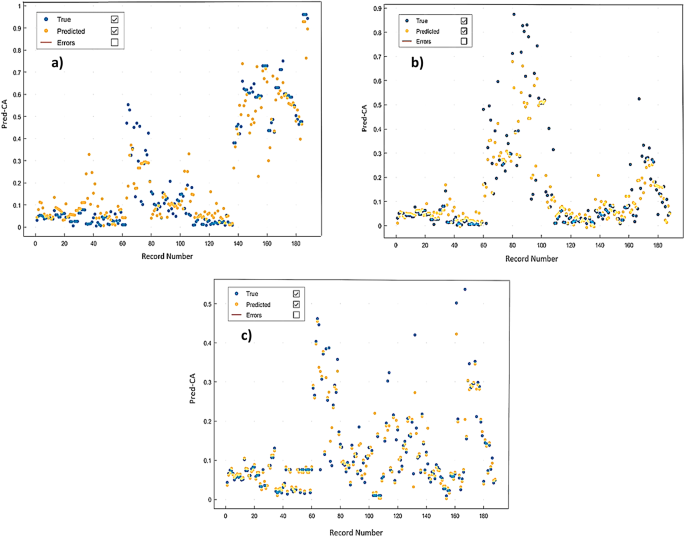
Cubic SVM response for: (a) ε=0; (b) ε=0.4; (c) ε=0.8 SVM modelling.
RBFN models results
RBF models adopted in this work had three layers: an input layer, a nonlinear hidden layer, and a linear output layer. The RBF network is used to develop predictions once it has been trained and its centers, radii, and weights have been specified. The RBF of the hidden layer neurons was implemented as a Gaussian function as:
$$:{varnothing:}_{i}left({left| {x – C_{i} } right|}right)={e}^{-left(frac{-{left({left| {x – C_{i} } right|}right)}^{2}}{{{r}_{i}}^{2}}right)},$$
(18)
where (:{varnothing:}_{i}) is the basis function ith hidden neuron, (:{r}_{i}) is the RBF radii, (:{c}_{i}) centers of the network and (:‖x-{c}_{i}‖🙂is the Euclidean distance. The structure of derivable purlin nonlinear function (:y) for the output layer with respect to the weights (:{w}_{i}) can be formulated as:
$$:y=sum:_{i=1}^{m}{w}_{i}{varnothing:}_{i}left({left| {x – C_{i} } right|}right)+b,$$
(19)
where (:{w}_{i}) are the synaptic weights linking the hidden layer to output neurons, b is the output neurons bias term. The cosine (:{varnothing:}_{i1}left(x.{x}_{i}right)) and Euclidean (:{varnothing:}_{i2}left({left| {x – x_{i} } right|}right)) distances have been proposed to be combined using a new kernel as follows:
$$:{varnothing:}_{i}left(x,{x}_{i}right)={{alpha:}_{1}varnothing:}_{i1}left(x.{x}_{i}right)+{{alpha:}_{2}varnothing:}_{i2}left({left| {x – x_{i} } right|}right),$$
(20)
where (:{alpha:}_{1}) and (:{alpha:}_{2}) are the fusion weights. At the nth learning iteration associated with a particular epoch. The overall mapping only considering Euclidean (:{varnothing:}_{i}left({left| {x – C_{i} } right|}right)) distances can be expressed as follows:
$$:{y}_{n}=sum:_{i=1}^{m}{w}_{i,n}{varnothing:}_{i}left({left| {x – C_{i} } right|}right)+{b}_{n},$$
(21)
Figure 10 shows the regression plots for different eccentricity levels ε=0, 0.4, and 0.8, giving overall relation coefficients R-values of 0.984, 0.978, and 0.971 and average absolute errors AAE-values of 1.1, 1.4 and 1.7, respectively.
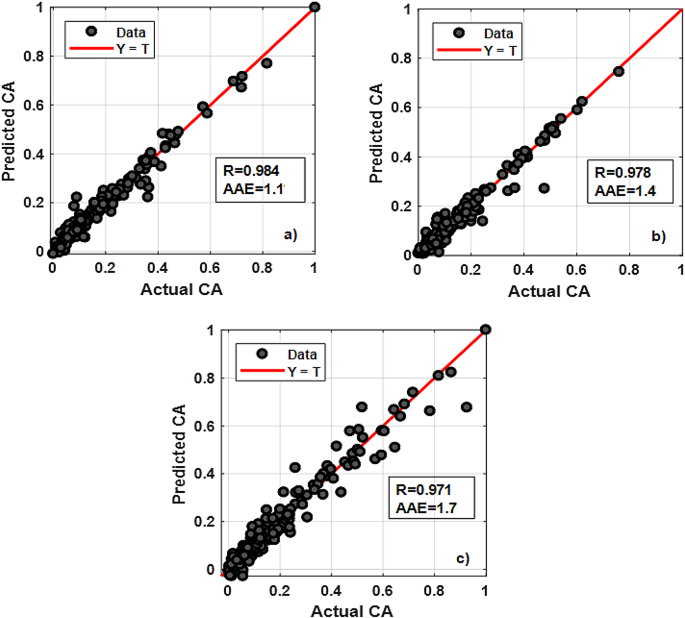
Regression plots for: (a) ε=0; (b) ε=0.4; (c) ε=0.8 RBFN modelling.
Furthermore, to comprehensively assess the performance and generalization capability of the RBFN model, additional statistical metrics were calculated, including root mean squared error (RMSE), mean absolute percentage error (MAPE), the coefficient of determination (R2), and adjusted R2. These metrics were computed across the training, validation, testing, and combined datasets using the denormalized predicted values as in Eqs. (16) through (19).
$$:MSE:=left(frac{1}{n}right){sum:}_{i=1}^{n}{left({CA}_{pred,i}-:{CA}_{act,i}right)}^{2},:$$
(22)
$$:MAPE:=:left(frac{100%}{n}right){sum:}_{i=1}^{n}left|frac{{CA}_{pred,i}-:{CA}_{act,i}}{{CA}_{act,i}}right|,$$
(23)
$$:{R}^{2}=:1:-frac{:{sum:}_{i=1}^{n}{left({CA}_{act,i}-:{CA}_{pred,i}right)}^{2}}{{sum:}_{i=1}^{n}{left({CA}_{act,i}-:{overline{CA}}_{act}right)}^{2}},$$
(24)
$$:Adjusted:{R}^{2}=:1:-:left(1:-:{R}^{2}right)*:left(frac{n:-:1}{n:-:p:-:1}right),$$
(25)
where (:{CA}_{pred,i}) is the predicted value of (:CA), (:{CA}_{act,i}) is the actual value of (:CA), is the number of samples and (:p) is the number of predictors (features).
These statistical metrics were computed across the training, validation, testing, and combined datasets using the denormalized predicted values for different eccentricity values ( ε= 0, 0.4, and 0.8) as listed in (Tables 6, 7 and 8).
Validation of proposed RBFN model
To validate the proposed RBFN model, it was used to predict CA in a real-world scenario while drilling new deviated test well located in the Gulf of Suez, Egypt. An overview of the lithological remarks, depth intervals, and actual hole cleaning indicators for well-x, are indicated in (Table 9). In addition, Fig. 11 depicts the utilization of RBFN model for the new validation well-x datapoints showing a high CA prediction accuracy for R-values = 0.987, 0.977 and 0.968 and AAE-values of 0.8, 1.97 and 1.6 for ε= 0, 0.4 and 0.8, respectively.
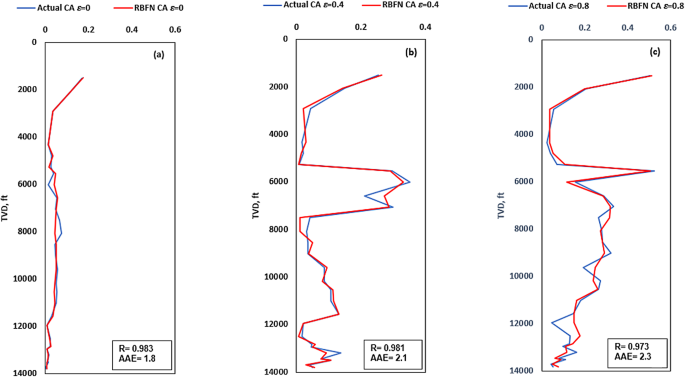
CA prediction using RBFN for neighbor test well application (0 to14000) ft depth interval: (a) CAε=0; (b) CAε=0.4; (c) CAε=0.8.
In validation with well-x, RBFN model performance is evaluated using the same two metrics (R and AAE) and tested under different values of ε= 0, 0.4, and 0.8. The results indicate that the RBFN model has high accuracy, as evidenced by the low AAE and high R values, which indicate small errors and good alignment between predicted and actual CA values.
These results from the development phase are very similar to this validation phase, indicating good generalization. The consistency between the development phase and the validation phase performance indicates that the model is not overfitting the training data, but rather generalizes well to unseen data, such as the validation well-x dataset. This makes the RBFN model robust and suitable for real-world applications, as it maintains high prediction accuracy even when tested on new datapoints not seen during training.
Same as in the development phase, a slight decrease in R values for ε= 0.8 (0.973 in validation) and (0.971 in development) compared to the other levels can be attributed to the increased complexity in the linear system caused by higher pipe hole eccentricity level increasing (Fig. 12). As eccentricity increases, the behavior of the system becomes more complex, which badly affects the RBFN model ability to generalize effectively. However, even with this drop, the model performance is still strong, indicating that it is able to handle a range of eccentricity values reasonably well.
Moreover, RBFN model exhibited consistently high performance across all cases, with R ranging from 0.988 to 0.996, and R2 values above 0.976, confirming strong predictive capability. Adjusted R2 values further confirmed the robustness of the model with minimal risk of overfitting. Moreover, the model achieved low RMSE, as low as 0.001, and MAPE under 6%, highlighting its accuracy and reliability. These results validate the generalizability of the RBFN model across varying operational conditions.
A detailed visualization of RBFN model performance presented in (Figs. 13, 14 and 15) showing bar charts of MSE per fold, boxplots of MSE distribution and performance curves across an overall validation dataset, respectively. Additionally, various statistical metrics to measure cross validation performance for each eccentricity level are summarized (Tables 10, 11 and 12), illustrating that no single fold exhibited significant degradation in predictive accuracy. This supports the reliability and robustness of the model under different data partitions.
The observed improvement over initial validation using a static (70, 15, 15%) data split underscores the value of k-fold cross-validation, particularly when dealing with datasets derived from limited operational diversity (six wells from a single basin). The enhanced stability and accuracy of the model reflect effective mitigation of overfitting and improved confidence in the real-world applicability of proposed RBFN model.
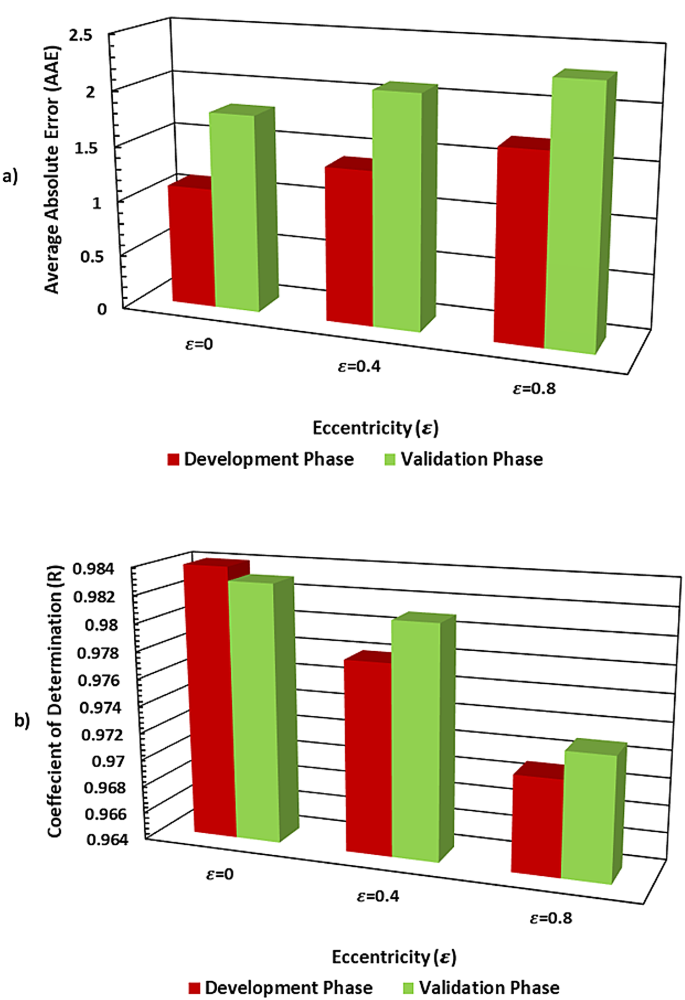
Statistical performance of the development and validation phases of RBFN models: (a) R values; (b) AAE values.
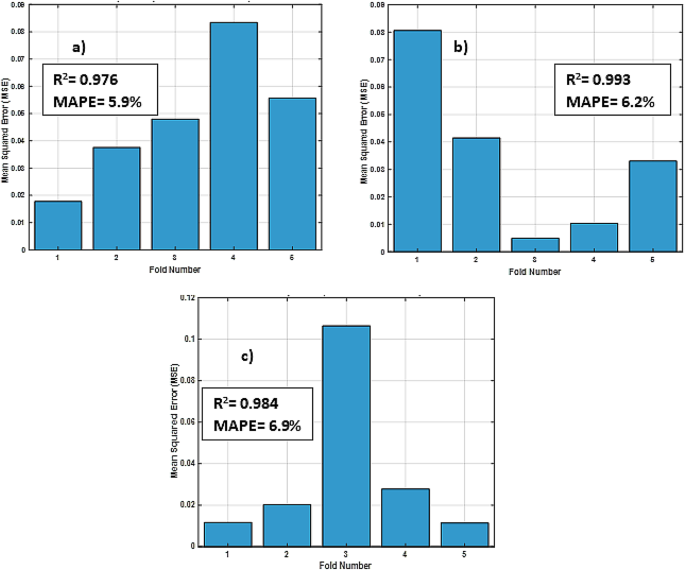
Bar charts of mean squared error (MSE) per fold of: (a) ε=0; (b) ε=0.4; (c) ε=0.8 for RBFN 5-fold cross-validation.
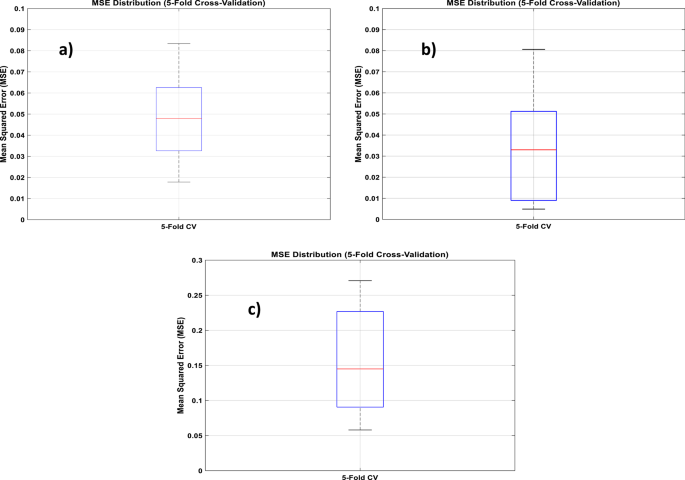
Box plots of mean squared error (MSE) per fold of: (a) ε=0; (b) ε=0.4; (c) ε=0.8 for RBFN 5-fold cross-validation.
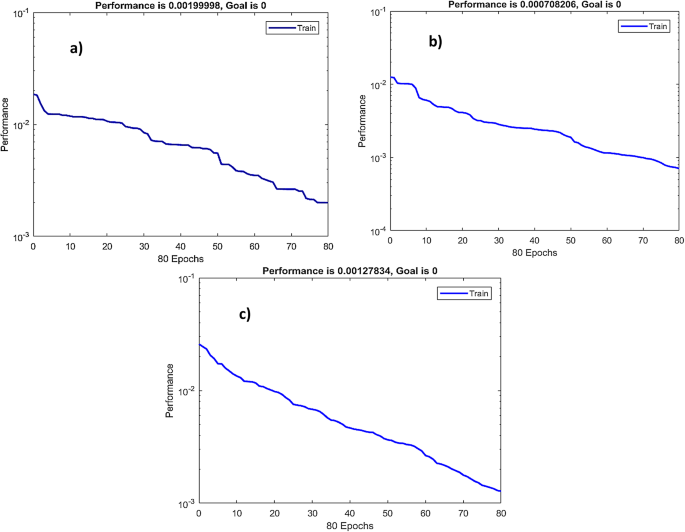
Performance curves RBFN 5-fold cross-validation of: (a) ε=0; (b) ε=0.4; (c) ε=0.8.
Feature importance and sensitivity for proposed RBFN model
To assess feature relevance and enhance model interpretability, a Permutation Feature Importance (PFI) analysis was conducted on the test dataset using the final trained RBF neural network (Fig. 16). This method estimates the contribution of each input feature by measuring the increase in prediction error (ΔMSE) after randomly permuting that features values, thereby disrupting its relationship with the target. This approach is well-suited for complex, nonlinear systems such as eccentric deviated hole drilling. PFI was evaluated for three pipe eccentricity conditions ε= (0, 0.4, 0.8) to understand how the influence of each input feature evolves with increasing eccentricity.
Across all cases, ECD remained the most important feature, with ΔMSE values ranging from (0.0044–0.0111), confirming its dominant role in predicting CA regardless of annular geometry. ROP and ρc were consistently ranked among the top three influential features in all conditions, with ΔMSE values around (0.0038–0.0047) and (0.0022–0.0042), respectively.
The increasing importance of features such as CCI and G with higher eccentricity levels suggests condition-specific interactions, where their influence becomes more pronounced under asymmetric or inclined flow conditions. This indicates that geometric and cuttings transport effects are more critical in deviated wells, and their inclusion in predictive models should be emphasized when modeling non-vertical or eccentric drilling environments.
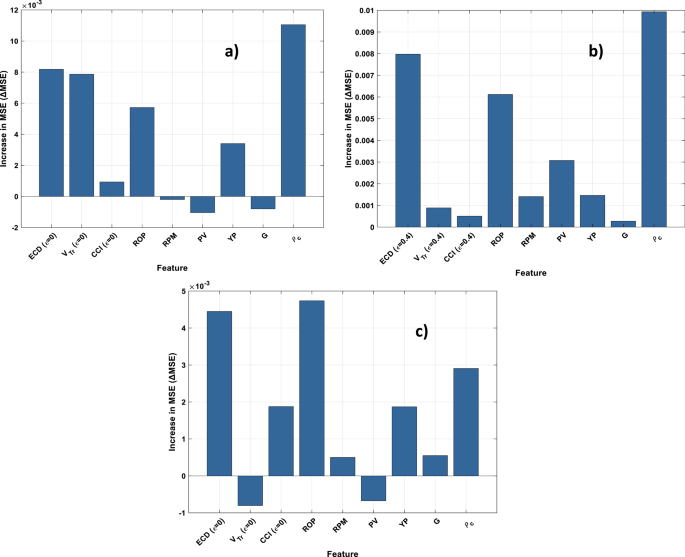
Permutation feature importance (PFI) on test set: (a) ε=0; (b) ε=0.4; (c) ε=0.8 for RBFN modelling.
To examine the statistical behavior and robustness of the proposed RBFN model across different eccentricity configurations, a Monte Carlo simulation was conducted. A total of 10,000 realizations were generated to evaluate the distribution characteristics of the predicted cuttings concentration (CA) at eccentricity levels (=0, 0.4 and 0.8). The simulation process was constructed by randomly sampling input variables from the normalized dataset using stratified random techniques to ensure representation of the full variability in the input space. These samples were then propagated through the trained RBFN model, and the outputs were recorded for statistical evaluation. Such simulation techniques have been previously validated in the literature for approximating the behavior of complex nonlinear systems where analytical solutions are challenging to derive59.
Following this, the cumulative distribution functions (CDFs) of the CA predictions were constructed for each eccentricity scenario. Three key percentiles—the 10th (P10), 50th (P50), and 90th (P90)—were calculated to characterize the spread, central tendency, and skewness of each output distribution. These percentiles were found to be aligned with theoretical expectations, where P50 represented the median and P10/P90 provided insight into the tail distribution of the model output. As illustrated in Fig. 17, the resulting CDFs for CA(0), CA(0.4), and CA(0.8) exhibit sigmoidal (S-curve) behavior, with most values concentrated around the median and relatively few extreme values at the tails.
At ε = 0, the CDF curve remains shallow, indicating a wider distribution with most predicted CA values clustered toward the lower end of the scale. As the eccentricity increases to ε = 0.4, the CDF becomes steeper and shifts to the right, representing an increased concentration of mid-range CA values and higher model confidence. This trend is further amplified at ε = 0.8, where the CDF curve is even steeper and levels off more rapidly, signifying that the model outputs are now tightly clustered at higher CA values. This progression confirms the model’s increasing predictive stability with greater eccentricity, as fewer outliers and a tighter output range are observed. Additionally, the upward shift in the P50 value from CA(0) to CA(0.8) quantitatively confirms the anticipated increase in CA with eccentricity, further validating the physical realism of the RBFN predictions.
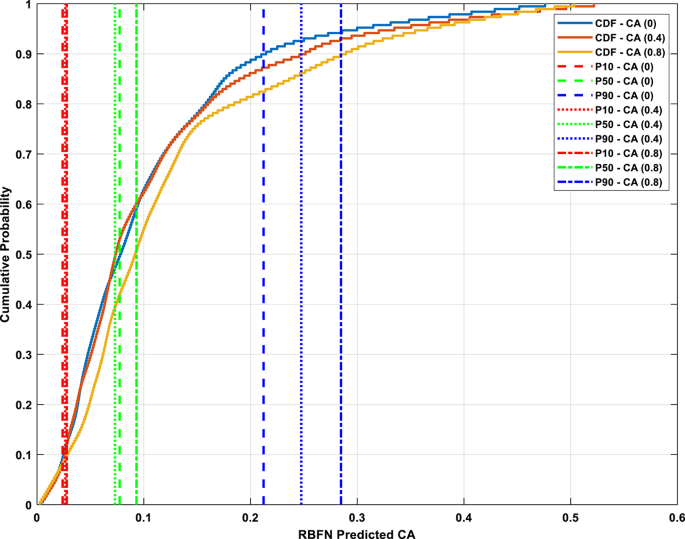
CDF plot of RBFN predicted CA with P10, P50, and P90 percentiles of (ε=0, 0.4 and 0.8) datasets.
The histogram of the simulated random data, normalized to a probability density function (PDF), revealed a close alignment with the expected normal distribution, confirming the validity of the assumption of normality. In the CA (0) histogram (Fig. 18a), high probability is concentrated at lower values near the left tail, which suggests that the system consistently produces low output values. The distribution is narrow and sharp, with probability peaks close to the lower end of the CA range. This means the RBFN output at low concentrations is highly stable and predictable. There is minimal variation, as most of the output values fall near the mean, indicating a high degree of certainty in the response at this level. For CA (0.4) (Fig. 18b), the probability for low CA decreases compared to CA (0). As the eccentricity level increases, the normal distribution fit (red curve) shifts towards the middle range, and the output values are more likely to fall closer to the mean of the medium concentration range, with less probability for lower CAs. Finally, for CA (0.8) (Fig. 18c), a good normal fit for high concentrations suggests that the high CAs predictions are controlled or have reached an equilibrium, with low variations and a tight clustering around the mean. Further, skewness approach minimal value (1.5758) typical for a normal distribution, indicating fewer extreme deviations and a bell-shaped curve.
Overall, across sensitivity analysis, we can conclude that data exhibit predictable, and well-controlled behavior with minimal noise or skewness, leading to a reliable analysis and high confidence in CA predictions. These findings align with previous sensitivity analysis in the field, where similar Monte Carlo approaches have been used to model and analyze random processes, providing valuable insights into the underlying distributions of predicted CA using proposed RBFN approach.
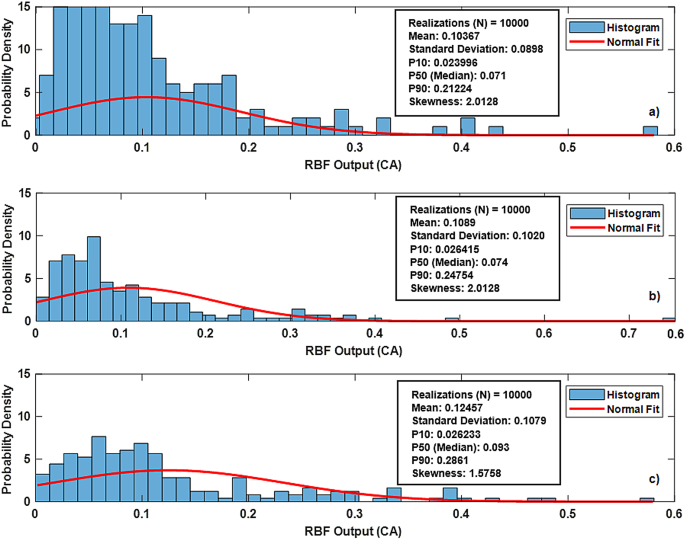
Histogram of Monte Carlo simulated RBFN output (CA) sample with normal distribution fit of (ε=0, 0.4 and 0.8) datasets.
Effect of intermediate features on model accuracy
We evaluated the performance of the RBFN model trained with raw features (Fig. 19), such as eccentricity level and (:{:rho:}_{m}), compared to the intermediate feature model. The model using raw features performed with overall R and AAE values of (0.981, 0.952 and 0.966) and 2.9, 1.9 and 1.8, for the three presumed levels, respectively (Fig. 20). This indicates that while the model using raw features had a strong performance, the results were not as optimal as those from the model incorporating intermediate features.
The intermediate features significantly enhanced the predictive power of the RBFN model, as shown by the higher R and lower AAE values. This highlights the importance of using well-chosen intermediate variables to improve the predictive model accuracy and CA prediction capabilities, especially in complex eccentric geometries where raw features alone may not fully capture the required patterns. The model incorporating intermediate variables (VTR, CCI, ECD) achieved an RMSE of 8.7, demonstrating a significant improvement in predictive accuracy.
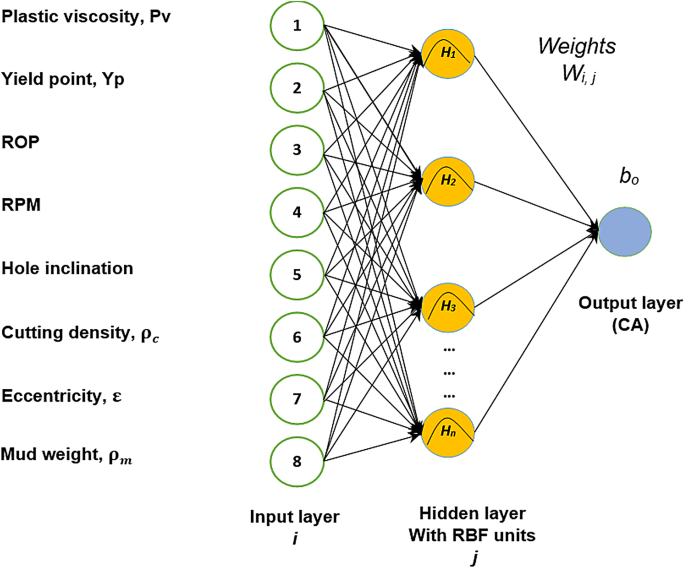
Architecture of RBFN model using raw data for CA prediction.
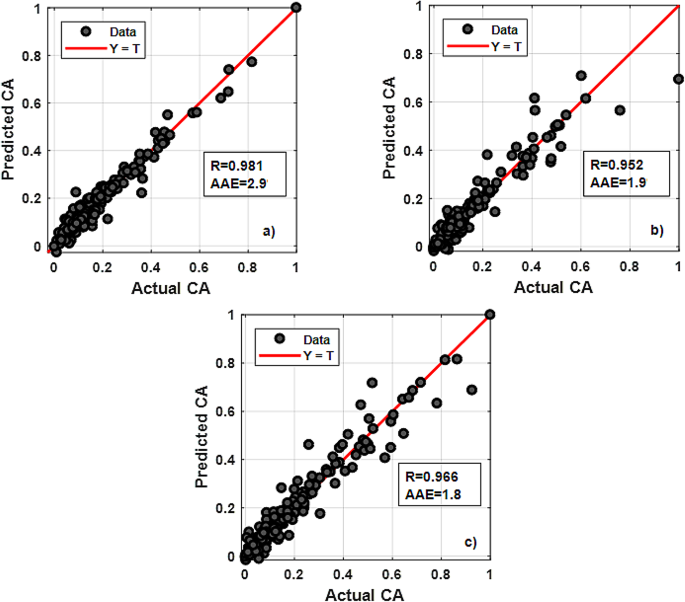
Regression plots of RBFN modelling using raw features for: (a) ε=0; (b) ε=0.4; (c) ε=0.8.
White box equations based on developed RBFN model
RBF output function can be formulated in terms of Euclidian distance coefficient (:{text{h}}_{text{i}}left(text{x}right)) Gaussian basis function as:
$$:{y}_{n}=sum:_{i=1}^{m}{w}_{i,n}{h}_{i}left({x}_{n}right):+{b}_{n},$$
(26)
where;
$$:{h}_{i}left({x}_{n}right)={e}^{left(frac{-{(x-{c}_{i})}^{2}}{{{r}_{i}}^{2}}right)},$$
(27)
Equation 18 can be solved by solving a system of linear equations using least squares method as:
$$:{[h}_{1}left({x}_{1}right){w}_{1}+{h}_{2}left({x}_{1}right){w}_{2}+dots:+:{h}_{9}left({x}_{1}right){w}_{9}]+{b}_{1}={y}_{1}::::$$
$$:left[{h}_{1}left({x}_{2}right){w}_{1}+{h}_{2}left({x}_{2}right){w}_{2}+dots:+:{h}_{9}left({x}_{2}right){w}_{9}right]+{b}_{2}={y}_{2}::::$$
$$:left[{h}_{1}left({x}_{n}right){w}_{1}+{h}_{2}left({x}_{n}right){w}_{2}+dots:+{h}_{9}left({x}_{n}right){w}_{9}right]+{b}_{n}={y}_{n},$$
(28)
Here, the design matrix W*H + b = y includes H coefficients on the left-hand side of the equation, the weight vector W added by the output layer bias b to produce the optimized output function y. The entire mathematical operation is repeated for every RBFN model for different eccentricities (0, 0.4, 0.8). An excerpt of RBFN centers (C) and coefficients (H) for each eccentricity model are listed in (Table 13).