In this study, machine learning algorithms are employed to develop multi-label forecasts of the PV and AC power output for a BAPV plant. Different groups of machine learning algorithms and datasets are proposed to apply the forecasting model to ensure the accuracy and reliability of these models. The proposed MLAs consist of neural-based methods, including neural networks (NN), deep learning (DL), regression-based methods (linear regression (LR), tree-based methods including gradient-boosted trees (GBT), random forests (RF), and decision trees (DT), lazy-based methods (K-NN), and finally support vector machines (SVM).
RapidMiner Studio’s graphical user interface software is used in the modeling implementation. RapidMiner is a data analytics software platform created in 2001 by Ralf Klinkenberg, Ingo Mierswa, and Simon Fischer18. It offers a range of operators and repositories for processes like data preparation, transformation, modeling, and evaluation. Specific functionality includes tools for process control and utilities, repository access, importing/exporting, data manipulation, and model building. This research utilized Rapid Miner Studio version 10.1 Educational edition. Its comprehensive toolset is aimed to support the end-to-end data science workflow, covering aspects such as parameter tuning, model training, validation, and performance evaluation.
Figure 2 shows the flowchart implemented in this study, comprising input, training, and forecasting phases. The input phase involves data collection, providing environmental inputs of solar irradiance, ambient temperature, wind speed, and cell temperature measured on-site. Recorded PV and AC power outputs are the data labels to be predicted. Data pre-processing, discussed in Sect. 3.2, is then conducted. This important step refines the inputs before modeling to improve accuracy. During training, machine learning algorithms are developed using the pre-processed, historical input-output datasets. Models learn the relationships between inputs and targets to perform forecasts.
The forecasting phase allows for predicting PV and AC power production into the future. As new, real-time data is collected daily, models are continuously trained and used to issue multi-horizon power generation forecasts. The dataset used in the study is one year in length, ranging from October 2022 to September 2023, representing all seasons of the year, including winter, with high fluctuation in solar radiation and prediction complexity.
After the raw data were pre-processed, feature selection techniques such as feature importance ranking and Pearson correlation were then applied to identify the most predictive independent variables to include in the models. The pre-processed data was divided into training, validation, and test subsets using split sampling with a 70:30 ratio for training and testing, respectively. Machine learning algorithms were trained on the training set to iteratively learn patterns in the data and optimize model parameters through multiple iterations. Concurrently, hyper-parameter tuning using the validation set helped configure aspects of model structure not learned during training, such as the number of hidden layers in an NN and the kernel number in SVM. Once fully specified, the trained machine learning models were evaluated on their predictive performance using previously unseen observations from the held-out test set, to objectively measure how well the models generalize to new data. This workflow helps develop robust and optimized statistical learning models for reliable predictive accuracy assessments.
As part of the supervised learning process, the models developed using each MLA experienced further refinement and performance evaluation on independent validation data. The internal parameters of the algorithms were fine-tuned to optimize predictive accuracy. A variety of error and correlation metrics were then computed to assess and compare forecast quality across MLAs. These included absolute error (AE), root mean square error (RMSE), normalized absolute error (NAE), relative error (RE), relative root square error (RRSE), and correlation coefficient (R).
Flowchart of the proposed ML-based power forecasting methodology.
The workflow steps are summarized as follows:
-
a)
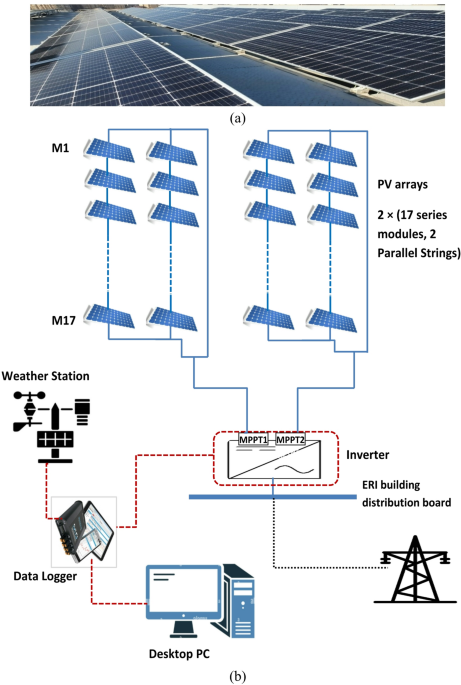
The PV plant data are collected through the weather station and data logger. This includes all meteorological data and measured outputs of the PV plant over one year with a 5-minute resolution.
-
b)
The data are prepared according to the required forecasting horizon (short, medium, or long-term).
-
c)
RapidMiner software is used to implement the MLAs. The data are retrieved for training and validation.
-
d)
Data filtering is performed to remove outlier values.
-
e)
Feature selection identified important input features and labels to predict.
-
f)
A data normalization technique is chosen based on the ML modeling approach.
-
g)
The pre-processed data was split into 70% for training and 30% for testing subsets.
-
h)
A multi-label machine learning models are applied to forecast AC power and PV power outputs.
-
i)
A validation model is then applied to a new dataset based on multiple time horizons to verify the model.
-
j)
The performance indicators of the model are evaluated and printed.
Environmental parameters and data collection
The relationship between meteorological factors and photovoltaic (PV) power output is location-dependent, dictated by geographical and climatic conditions. Consequently, the degree of correlation between weather inputs and PV generation differs between sites. However, forecasting model accuracy hinges on the input-output correlation structure19, and a site-tailored approach is necessary. Different factors affect PV forecasting accuracy, making such predictions a sophisticated process. It depends on factors such as forecasting horizons, forecast model inputs, and performance estimation20.
Meteorological parameters play a pivotal role in PV power forecasting performance, as they directly influence generation levels. The most significant input is solar irradiance, followed by ambient temperature, as both are strongly correlated with PV output. The movement of clouds also determines sudden and abrupt changes in PV power production. This study selects all key meteorological factors that comprehensively represent site conditions as input features. Solar irradiance is the dominant parameter, given its direct energy relationship. Ambient temperature further impacts efficiency, especially at higher levels. Cell temperature and wind speed round out the input set. The performance of a prediction model is directly affected by the season of the year4; thus, seasonal effects necessitate balanced data representation during model training. As performance varies by weather patterns throughout the year, an equally distributed dataset covering all four seasons was used. This improves model generalization beyond any single season and avoids bias. Also, optimizing input selection is important to maximize accuracy while constraining computational overhead. In this case, all primary meteorological drivers are incorporated as inputs to provide a holistic view of influencing conditions impacting PV generation. Seasonal weighting also strengthens model robustness.
In this study, the meteorological data are measured from Oct 2022 to Sept 2023. This dataset comprises eight attributes, including date, time, radiation, ambient temperature, wind speed, cell temperature, PV power, and AC power. Data was recorded via the data logger at five-minute intervals (comprising more than 105 K data samples per parameter). The initial dataset is split to be trained and tested (70%-30%). The original dataset is measured every 5-minute record, hourly, and daily measurements. In this study, all meteorological parameters that affect PV production are selected as input features; this includes solar irradiance as a dominant parameter, ambient temperature as the second factor that has an impact at high temperatures, cell temperature, and finally wind speed. The PV power and AC power are selected as the targets for the multi-label machine learning model.
Figure 3 demonstrates the variation in meteorological parameters and cell temperature over the selected year of the study. Solar irradiance changes from 0 to 1000 W/m2, with some minor readings up to 1200 W/m2 under clear weather conditions, especially in April and May. Ambient temperature varies from 10 to 44 °C, with minimum night temperatures near 10 °C and maximum daily temperatures approaching 44 °C. Cell temperature spans 10–68 °C. Wind speed fluctuates from 1 to 9 m/s, with repeating values at low levels, as Cairo has typical moderate to low wind speeds. Before modeling, this dataset goes through pre-processing to improve model accuracy. Pre-processing includes two main processes: filtration and data normalization. Outlier filtration removes odd readings while data normalization scales variables to the same measurement units, positioning data for optimal training. The appropriate data normalization methodology was selected according to the machine learning approach. As shown in Fig. 3, environmental patterns exhibit substantial seasonal and daily fluctuations influencing PV generation levels.
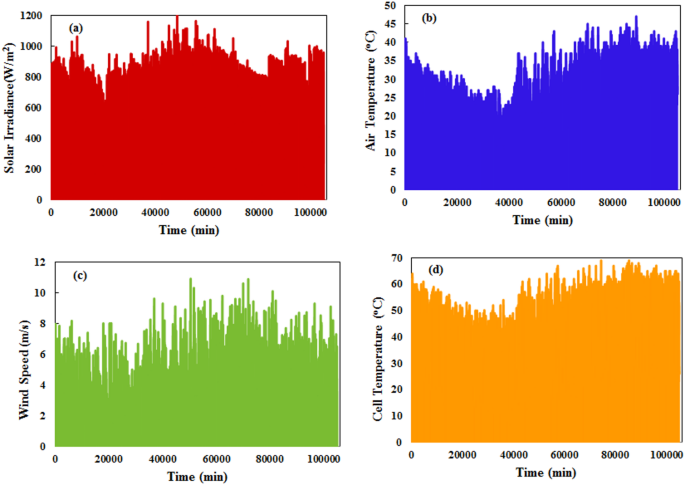
Full-year meteorological data recordings (a) Srad (b) Tamb, (c) Ws, and (d) Tcell.
Feature selection
Feature selection is an important step to identify the most influential input variables and discard irrelevant or redundant features. This helps develop a suitable feature subset for the model while improving performance and interpretability. In this study, the Pearson correlation coefficient6 was used to evaluate the relationship between each input predictor variable and the target (label) variable, due to the inherent characteristics of PV data. R is a widely applied metric of linear correlation between two quantitative variables, with a value between − 1 and 1. It indicates both the direction and magnitude of association – whether an increase in one variable tends to be accompanied by an increase or decrease in the other. Mathematically, the R between a feature x and target y is defined as the covariance of the two variables divided by the product of their standard deviations21,22:
$$:R=frac{sum:left({x}_{i}-bar{x}right)left({y}_{i}-bar{y}right)}{sqrt{sum:{left({x}_{i}-bar{x}right)}^{2}sum:{left({y}_{i}-bar{y}right)}^{2}}}$$
(1)
Where, (:{x}_{i}) and (:bar{x}) are the values and the mean of the x-variable in a dataset, respectively, (:{y}_{i}) and (:bar{y}) are the values and the mean of the y-variable in a dataset, respectively. In our case, (:{x}_{i}) represents input features (Srad, Tamb, Ws, and Tcell), while y represents output labels to be predicted (PPV, and PAC).
Data pre-processing
Input solar power and meteorological data require pre-processing to enhance model accuracy and improve computational efficiency. Raw datasets may contain transient spikes and non-stationary components due to unpredictable weather. Issues like outliers, sparsity, and abnormal records are common and can interfere with modeling patterns. Pre-processing aims to refine datasets before ML model development. A series of filtering steps was applied to both photovoltaic power output and meteorological data. First, physically improbable values such as negative numbers, null readings due to sensor errors, or periods of missing sensor recordings were removed. Streamlining datasets aimed to reduce improper training problems and computational costs from irregularities, outliers, and irrelevant inputs. Providing full high-resolution datasets, including night-time null PV values, could negatively impact training and accuracy due to data sparsity. To address this, the night-time sampling frequency was reduced without a complete removal. Filters removed implausible outliers and days with extensive missing values.
In our study, a filtration strategy was applied to remove negative irradiance values, ensuring data consistency. Additionally, sparse night-time data, where PV power is null, was identified as a potential factor affecting model performance. To address this, the night-time dataset was reduced but not eliminated, as these data points represent the cyclic behavior of solar irradiation absence, which is essential for capturing realistic system dynamics. Furthermore, days with insufficient data records were filtered out to maintain dataset integrity and prevent inconsistencies during model training. By thoroughly cleaning and conditioning the datasets before model development, this strategy helped minimize potential training issues and computational burdens that incomplete or improper inputs may introduce. Pre-processing steps aimed to remove faulty inputs, address sparsity, isolate consistent patterns, and balance dataset properties for optimized machine learning. This facilitated proper learning of historical trends and enhanced forecasting performance.
The second step after applying filtration is data normalization. This study implements two data normalization techniques: range transformation and z-transformation. The selection criterion was based on the proposed machine learning algorithm. Range transformation normalized data to a fixed range between 0 and 1. In the range normalization technique, the input data are rescaled to fall within a smaller common range from their original wider range. Specifically, all variables are scaled between 0 and 1. This approach helps reduce regression errors by restricting values to a narrow interval while maintaining correlations between input parameters. It prevents variables with inherently high values from dominating those with smaller scales. Normalizing data in this way further allows machine learning algorithms to treat each feature equally during training, improving both training speed and convergence. Variables standardized to the same scale can then be directly compared in terms of their relative impact.
Mathematically, the min-max scalar transforms data according to the formula23:
$$:widehat{zs}=frac{zi-{z}_{min}}{{z}_{max}-{z}_{min}}$$
(2)
Where,(::widehat{zs}) is the scaled value, (:zi) is the measured value, (:{z}_{max}) and (:{z}_{min}) are the maximum and the minimum values of the dataset.
Range normalization rescales input data to a standardized interval; it transforms a wider range of data values into a restricted range between zero and one. In this study, the “min-max scalar” method is employed for range normalization. This normalization provides data rescaling to a constrained range that minimizes regression errors, preserves correlations within datasets, and improves precision. Moreover, range normalization addresses scale differences among input features that could otherwise dominate the modeling process. By standardizing to a common scale, variances in value magnitudes between parameters are mitigated. As a result, all inputs can be treated equally during training without some features overriding others. This optimized weighting boosts algorithm calculation speeds and convergence. The range normalization is used for all models tested in this study except support vector machines.
SVM instead used z-transformation, which standardizes variables by removing the mean and scaling them to unit variance. Compared to min-max normalization, the z-score transformation provides more accurate predictive results when using SVMs. The approach of standardizing by mean and variance yields superior model performance for SVMs versus other machine learning algorithms. This processing fits the SVM algorithm, which relies on calculating distances between samples. This normalization is a commonly used technique to standardize data values. It transforms values by subtracting the original mean and dividing by the standard deviation. The result is distributed data with a mean of 0 and a standard deviation of 1. This preserves the original shape of the distribution while making values dimensionless and comparable on the same scale24.
The z-score normalization formula applied to each value in the dataset is:
$$:widehat{zt}=(zi-mu:)/sigma:i$$
(3)
Where, (:mu:) is the mean of the data, and (:sigma:i) is the standard deviation of the data.
Machine learning algorithms
Function-based algorithms
Regression analysis is a statistical method used for numerical prediction. It quantifies the relationship between a dependent or target variable (i.e., the label attribute) and multiple independent variables (regular attributes)25,26.
There are various regression techniques; two are used in this research:
-
a.
Linear regression (LR)
LR fits a straight line to capture the linear relationship between the dependent and independent variables. It models the observed data with a linear Eqs.25,26. The mathematical model that represents the I-V characteristics of PV as a function of (Srad, Tamb, Ws, and Tcell) is given by:
$$:{P}_{PV}=eta::A:{text{S}}_{text{r}text{a}text{d}}:left(1-{beta:}_{T}left({T}_{cell}-{T}_{ref}right)right)(1-alpha:{W}_{s})$$
(4)
The mathematical representation of PV predicted power using LR is as follows:
$$:{P}_{PV}={beta:}_{0}+{beta:}_{1}{text{S}}_{text{r}text{a}text{d}}+{beta:}_{2}{text{T}}_{text{a}text{m}text{b}}+{beta:}_{3}{W}_{s}+{beta:}_{4}{T}_{cell}+ϵ$$
(5)
Where Srad, Tamb, Ws, and Tcell are input features. (:{beta:}_{0}) is the model intercept, (:{beta:}_{1},:{beta:}_{2},:{beta:}_{3},:{beta:}_{n}) are the predictor coefficients. (epsilon) is the error term.
-
b.
Polynomial regression (PR)
PR extends linear regression by incorporating nonlinear terms when the actual relationship is curved. It fits nth-order polynomial functions to the data (e.g., quadratic, cubic, etc.)27,28. The mathematical representation of PV predicted power using PR is as follows:
$$:{P}_{PV}::=genfrac{}{}{0pt}{}{{{beta:}_{0}+:beta:}_{1}{text{S}}_{text{r}text{a}text{d}}++{beta:}_{2}{S}_{rad}^{2}{+beta:}_{3}{text{T}}_{text{a}text{m}text{b}}+{beta:}_{4}{T}_{amb}^{2}+{beta:}_{5}{W}_{s}+{beta:}_{6}{W}_{s}^{2}{+beta:}_{7}{T}_{cell}{+beta:}_{8}{T}_{cell}^{2}}{begin{array}{c}{+beta:}_{9:}{{(text{S}}_{text{r}text{a}text{d}}:.:text{T}}_{text{a}text{m}text{b}}left){+beta:}_{10:}{{(text{S}}_{text{r}text{a}text{d}}:.:text{T}}_{text{c}text{e}text{l}text{l}}right){+beta:}_{11:}{{(text{S}}_{text{r}text{a}text{d}}:.:text{W}}_{text{s}}left){+beta:}_{12:}{({text{T}}_{text{a}text{m}text{b}}:.:text{T}}_{text{c}text{e}text{l}text{l}}right)\:{+beta:}_{13:}{({text{T}}_{text{a}text{m}text{b}}:.:text{W}}_{text{s}}left){+beta:}_{14:}{({text{T}}_{text{a}text{m}text{b}}:.:text{T}}_{text{c}text{e}text{l}text{l}}right){+beta:}_{13:}{({text{T}}_{text{a}text{m}text{b}}:.:text{W}}_{text{s}}left){+beta:}_{14:}{({W}_{text{s}}:.:text{T}}_{text{c}text{e}text{l}text{l}}right)+ϵend{array}}$$
(6)
Artificial neural network-based algorithms
Artificial neural networks (ANNs) are computational models inspired by biological neural circuits in the brain. An ANN contains interconnected units called neurons that process information via weighted links resembling synapses. Most commonly, ANNs are adaptive systems that can change their structure based on information flow during training. This enables them to model complex input-output relationships and discover hidden patterns in data. A feed-forward neural network is a basic ANN architecture where connections only transmit information in one direction, from input to output nodes, without cycles. Within this acyclic flow, data passes through one or more hidden layers of nodes that help extract higher-level features. During learning, feed-forward networks are presented with training examples, and weights are adjusted iteratively via back-propagation of error signals to minimize loss. This allows the network to gradually tune its synapse-like parameters until it can accurately map new inputs to predicted outputs29.
The back-propagation algorithm is a supervised learning technique for neural networks composed of two primary phases – propagation and weight updating. These phases operate through iterative training cycles. During propagation, input data is fed forward through the network to generate output predictions. The output values are then compared to true targets using an error function to quantify performance. Error signals derived from this analysis are then propagated backward through the network. This initiates the weight updating phase, where connection weights between nodes are adjusted in a direction that reduces the overall error. Repeated application of these two phases typically drives the network towards a stable state of minimal error, indicating it has learned the underlying relationships in the training data26.
A multilayer perceptron (MLP) is a type of artificial neural network well-suited for classification and regression problems. It employs a feed-forward architecture with one or more hidden layers of nodes situated between the input and output layers. All nodes are interconnected via bidirectional connections trained with back-propagation. Each node applies a nonlinear activation function, commonly sigmoid, to introduce nonlinearity. This allows MLPs to learn complex patterns across large input spaces30,31. In this work, two NN-based algorithms are implemented, which are:
-
a.
Neural network
The ML model architecture used in this study is a feed-forward multi-layer perceptron NN trained with a back-propagation algorithm. Within this framework, a standard sigmoid activation function is applied to the nodes. To suit the range expected by the sigmoid function, all input attributes were normalized to scale between − 1 and 1 using a normalization preprocessing step. Moreover, the output node uses either a sigmoid or linear activation function depending on the type of problem. Specifically, a sigmoid output activation was used since the task involves forecasting/classifying a variable, which represents a classification problem. On the other hand, a linear activation would be more appropriate for numeric regression tasks where the exact target value is to be predicted32,33. The mathematical representation of PV predicted power using NN is as follows:
$$:{P}_{PV}={f}_{text{out:}}left(sum:_{j=1}^{n}:{omega:}_{j}^{left(2right)}cdot:{f}_{text{h:}}left(sum:_{i=1}^{m}:{omega:}_{ij}^{left(1right)}{x}_{i}+{b}_{j}^{left(1right)}right)+{b}^{left(2right)}right)$$
(7)
-
b.
Deep learning
The deep Learning model34,35,36, in this work, is based on a multi-layer feed-forward artificial neural network that is trained with stochastic gradient descent with back-propagation. The deep Learning algorithm in Rapidminer uses H2O optimization18. The network contains a large number of hidden layers consisting of neurons with tanh, rectifier, and max-out activation functions. The mathematical representation of PV predicted power using DL is as follows:
$$:{P}_{PV}={f}_{text{out:}}left({{upomega:}}^{left(Lright)}cdot:{f}^{(L-1)}left({{upomega:}}^{(L-1)}cdot:dots:{f}^{left(1right)}left({{upomega:}}^{left(1right)}cdot:text{X}+{text{b}}^{left(1right)}right)+{text{b}}^{(L-1)}right)+{text{b}}^{left(Lright)}right)$$
(8)
Where X is (Srad, Tamb, Ws, and Tcell), (:L) Total number of layers in the deep neural network. (:varvec{upomega:}) is the weight matrix for layer i. (:{text{b}}^{left(iright)})is the bias vector for layer i. (:{f}^{left(iright)}) and (:{f}_{text{out:}})are activation functions for layer i and the output layer, respectively.
Trees-based algorithms
-
a.
Decision tree
A decision tree is a tree-based model that uses a hierarchical approach to classify or estimate target variables based on a set of input features or independent variables. The model contains a root node, internal decision nodes, and leaf nodes18. At each internal node, the data is split using a decision rule based on the value of a single predictive variable. The split separates the data into two or more homogeneous sets to be directed to the next child nodes. New child nodes are recursively generated from parent nodes until a stopping criterion is reached, such as a perfect split or a predefined depth limit. Predictions are determined depending on the majority class (for classification) or average value (for regression) within each terminal leaf node. For regression problems, the goal is to reduce the error of predicting a numerical target variable in the most optimal way. The hierarchical structure allows decision trees to model complex relationships between features and uncover interaction effects that may improve prediction performance. The mathematical representation of PV predicted power using DT is as follows:
$$:{P}_{PV}=sum:_{i=1}^{N}:{c}_{i}cdot:Ileft(text{X}in:{R}_{i}right)$$
(9)
Where (:{R}_{i}) is a region in the feature space where the ith rule applies.(::{c}_{i}) is a predicted constant value for the region (:{R}_{i}). (:Ileft(text{X}in:{R}_{i}right)) is an indicator function, which is 1 if (:text{X}) belongs to the region (:{R}_{i}) and 0.
-
b.
Random forest
A random forest is an ensemble method that trains multiple decision trees on bootstrapped subsets of the original training data. The number of trees comprises a hyper-parameter called the “number of trees”. During training, each tree node represents a rule for splitting the data based on the optimal values of a random subset of predictors. This splitting criterion aims to reduce errors in target value estimation.
New nodes are recursively added in this splitting manner until meeting the stopping criteria. Only a fraction of available features specified by the “subset ratio” is considered at each potential split point to minimize correlation between trees. Once fully grown, the forest combines the predictions of its constituent trees via averaging (regression). This introduces diversity that mitigates over-fitting to any single training sample or feature subset, resulting in an accurate and robust predictive model37,38,39,40.
The mathematical representation of PV predicted power using RF is as follows:
$$:{P}_{PV}=frac{1}{T}sum:_{t=1}^{T}:{P}_{PV}^{left(tright)}$$
(10)
$$:{P}_{PV}^{left(tright)}=sum:_{i=1}^{Nleft(tright)}:{{c}_{i}}^{left(tright)}cdot:Ileft(text{X}in:{{R}_{i}}^{left(tright)}right)$$
(11)
Where (:T)is the total number of DTs in the RF. (:{P}_{PV}^{left(tright)}) is the prediction from the tth DT, which is computed using the rules of that tree.
(:{{c}_{i}}^{left(tright)}) is the constant value predicted by the tth tree for the region (:{{R}_{i}}^{left(tright)}). (:Ileft(text{X}in:{{R}_{i}}^{left(tright)}right)) is the Indicator function for whether (:text{X}) belongs to the region (:{{R}_{i}}^{left(tright)}). (:{{R}_{i}}^{left(tright)}) is a region i of the feature space defined by the tth tree.
-
c.
Gradient-boosted trees
GBT is an ensemble learning technique that builds and combines weak prediction models sequentially to optimize predictive performance41. Like other boosted tree algorithms, it trains a series of decision tree models on adjusted versions of the training data. Specifically, trees are added one by one to minimize a differentiable loss function via gradient descent, providing a more structured and interpretable approach compared to other boosted tree techniques. This gradual, error-focused learning procedure improves the accuracy and controls the complexity of the trees to avoid over-fitting. While slower than a single model, the ensemble of tweaked decision trees combines to perform better than any single estimator42,43,44,45. The mathematical representation of PV predicted power using GBT is as follows:
$$:{P}_{PV}={F}_{M}left(text{X}right)=sum:_{m=1}^{M}:eta:cdot:{T}_{m}left(text{X}right)$$
(12)
Where (:M) is the total number of trees in the model.(::{T}_{m}left(text{X}right),:)prediction from the (:{M}^{th}) decision tree.(::eta:) is the learning rate.
Lazy-based algorithms
Lazy learning algorithms, also known as instance-based algorithms, make predictions based on similarity to previously stored examples or instances, without explicit generalization.
-
a.
k-Nearest neighbor
The most common lazy learning model is the k-nearest neighbor (k-NN) algorithm. The k-NN algorithm makes predictions based on the closest training examples in a feature space46. During training, k-NN simply stores the feature vectors and corresponding target values and does not perform any explicit generalization. To classify a new example, k-NN finds the k closest examples already stored (based on a distance measure like Euclidean) and predicts the most common class among those neighbors. For regression, it averages the target variable values of the nearest neighbors to forecast a continuous value. Nearer neighbors may be weighted more heavily to influence the prediction. Feature values are often normalized before distance calculations to avoid biases from variations in scale. In this paper, common preprocessing min-max scaling is applied. An advantage of k-NN is that it is simple to implement and understand. A disadvantage is that it requires lots of memory to store all training examples and has a high computational cost for classification16,47,48,49,50. The mathematical representation of PV predicted power using K-NN is as follows:
$$:{P}_{PV}=frac{1}{k}sum:_{i=1}^{k}:{P}_{PV}^{left(iright)}$$
(13)
For each training data, compute the distance (:dleft(text{X},{text{X}}_{i}right)) between the features and the training point. A common distance metric is Euclidean distance, which is given by:
$$:dleft(text{X},{text{X}}_{text{i}}right)=sqrt{{left({text{S}}_{text{r}text{a}text{d}}-{text{S}}_{text{r}text{a}text{d},text{i}}right)}^{2}+{left({text{T}}_{text{a}text{m}text{b}}-{text{T}}_{text{a}text{m}text{b},text{i}}right)}^{2}+{left({text{T}}_{text{c}text{e}text{l}text{l}}-{text{T}}_{text{c}text{e}text{l}text{l},text{i}}right)}^{2}+{left({text{W}}_{text{s}}-{text{W}}_{text{s},text{i}}right)}^{2}}$$
(14)
Support vector machine-based algorithms
The model in this work uses the mySVM software package developed by Stefan Ruping for support vector machine (SVM) modeling. Specifically, it utilizes mySVM’s Java-based implementation, which restricts SVM modeling to a linear kernel function18. However, this linear kernel approach results in a parsimonious SVM model that only contains the linear coefficient terms. This more compact representation allows for faster deployment and application of the trained model compared to other SVM kernel types that have greater complexity. By leveraging mySVM’s efficient linear SVM formulation, the proposed methodology aims to balance predictive accuracy with reduced computational overhead for practical solar power forecasting applications. The mathematical representation of PV predicted power using SVM is as follows:
$$:{P}_{PV}={{upomega:}}^{T}text{X}+b$$
(15)
Where (:text{X}) is the feature vector. (:b) is a bias term that shifts the decision boundary. (:varvec{upomega:}) is a weight vector orthogonal to the decision hyperplane.
Performance indices
In order to evaluate the performance of each machine learning algorithm (MLA) used in this work and assess their predictive accuracy, various statistical metrics are employed. These metrics include the absolute error (AE), root mean square error (RMSE), normalized absolute error (NAE), relative root square error (RRSE), and correlation coefficient (R). The Absolute Error is the default function of the RapidMiner software51.
$$:AE=:{y}_{p}-{y}_{i}$$
(16)
$$:RMSE=sqrt{frac{1}{n}:sum:_{t=1}^{n}{left(frac{left({y}_{p}-{y}_{i}right)}{{y}_{i}}right)}^{2}}$$
(17)
$$:RE=frac{left({y}_{p}-{y}_{i}right)}{{y}_{i}}:$$
(18)
$$:NAE=frac{1}{n}:sum:_{t=1}^{n}left|frac{left({y}_{p}-{y}_{i}right)}{{y}_{i}}right|$$
(19)
$$:RRSE=sqrt{frac{sum:_{i=1}^{n}:{left({y}_{p}-{y}_{i}right)}^{2}}{sum:_{i=1}^{n}:({y}_{i}-stackrel{-}{y}{)}^{2}}}$$
(20)
Where (:{y}_{i}) is the measured power value, (:{y}_{p}) is the predicted power value.