Pseudo-telepathy games, intriguing thought experiments in quantum mechanics, challenge our classical understanding of information and correlation, and now, researchers are rigorously quantifying their power. Gábor Homa, András Bodor, and József Zsolt Bernád, all from the HUN-REN Wigner Research Centre for Physics, present a detailed comparison of these games, including the well-known Mermin-Peres magic square and the doily game, with established tests of quantum mechanics known as Bell inequalities. Their analysis reveals how effectively these games demonstrate quantum contextuality, the idea that measurement outcomes depend on the context in which they are performed, and importantly, demonstrates that while conceptually appealing, Bell inequalities currently offer a more comprehensive way to reveal quantum effects within the studied two-qubit systems. This work establishes a clearer understanding of the relationship between these different approaches to exploring the foundations of quantum mechanics, and highlights the strengths and limitations of each.
Quantum Games Reveal Entanglement’s Limits
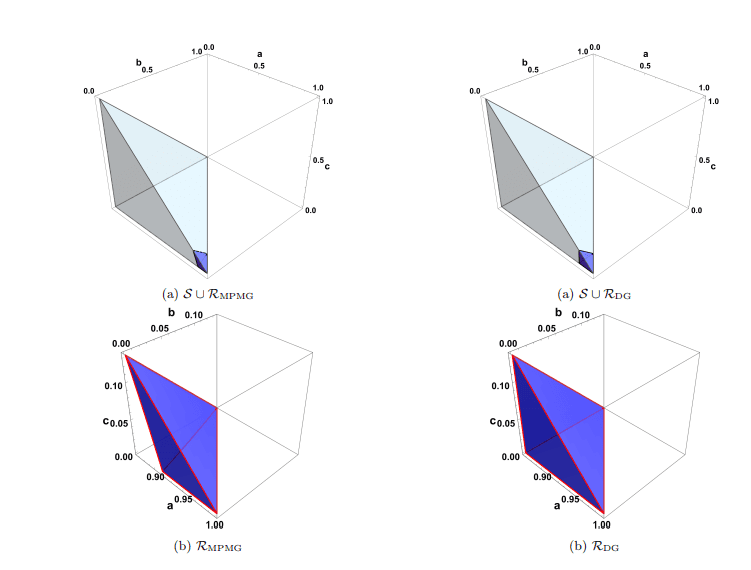
Quantum pseudo-telepathy games, such as the Mermin, Peres magic square and the doily game, theoretically allow players to achieve perfect scores when employing quantum strategies, contrasting with the limitations of classical strategies. Researchers quantitatively compare these games with Bell inequalities, exploring the relationship between non-locality and the ability to achieve perfect correlation, and determining the maximum advantage achievable and the required strength of quantum entanglement. The analysis reveals that certain game configurations exhibit a stronger connection to Bell inequalities than others. When using entangled quantum strategies, researchers quantitatively characterise the quantum advantage in these games and compare it with violations of the Clauser-Horne, Shimony, Holt and the Collins, Gisin inequalities. The analysis focuses on modified Werner states and Bell-diagonal states, identifying and quantifying the regions of quantum state space exhibiting either a quantum advantage or a Bell inequality violation. Within these families, the doily game captures a larger fraction of entangled states than the Mermin, Peres magic square game, though both are significantly limited.
Quantum Entanglement Violates Local Realism Experimentally
Research consistently demonstrates the conflict between quantum mechanics and local realism, a cornerstone of classical physics. Bell’s theorem predicts that quantum entanglement leads to correlations impossible to explain by theories assuming objects possess definite properties independent of measurement, and numerous experiments have now verified these predictions, confirming the non-local nature of quantum mechanics. These experiments explore concepts like contextuality, where the value of a quantum observable depends on other simultaneous measurements. Quantum pseudo-telepathy games and magic games demonstrate this non-locality in a unique way, appearing to allow entangled particles to communicate instantaneously. Researchers investigate entanglement and separability, recognising entanglement as a crucial resource for quantum information processing and a key ingredient in violating Bell inequalities. Recent experiments, utilising increasingly sophisticated quantum computers, aim to demonstrate quantum advantage, showing that quantum devices can perform tasks impossible for classical computers.
Game Advantage and Bell Inequality Violation Regions
This research quantitatively compares the advantage gained in the Mermin-Peres magic square and the doily game with the degree of violation observed in the Clauser-Horne-Shimony-Holt and Collins-Gisin inequalities. The analysis focuses on modified Werner states and Bell-diagonal states, mapping the regions within these state families where either a game advantage or a Bell inequality violation occurs. Results demonstrate that the doily game encompasses a larger fraction of states exhibiting an advantage than the Mermin-Peres game, though both are ultimately limited compared to the broader regions where Bell inequality violations are observed. The team’s findings indicate that, within the examined state families, Bell inequalities are generally more effective at revealing non-classical behaviour than the pseudo-telepathy games. While both approaches are fundamentally linked to the concept of contextuality, the Bell inequalities consistently identify a larger set of states demonstrating non-classicality. This research contributes to a deeper understanding of the connection between quantum nonlocality, contextuality, and the limits of classical behaviour, offering insights into the foundations of quantum mechanics.