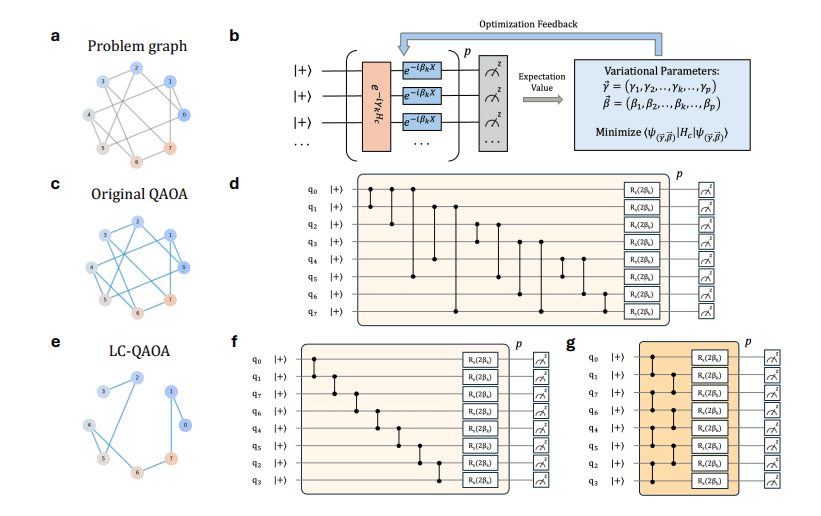
Combinatorial optimisation presents a significant challenge across diverse fields, and quantum computing offers the potential for substantial speed improvements over classical approaches. Zixu Wang, Jack Mandell, Yangyang Xu, and Jian Shi, from Rensselaer Polytechnic Institute, investigate the Quantum Approximate Optimisation Algorithm (QAOA), a promising technique for achieving quantum advantage on current and near-future quantum hardware. Recognising that the circuit complexity of standard QAOA rapidly becomes unmanageable as problem size increases, the team proposes a novel approach termed the ‘linear chain ansatz’. This new method constructs quantum circuits with a depth independent of problem size, dramatically reducing computational demands and enabling the tackling of much larger optimisation problems, demonstrated through achieving a 0. 78 approximation ratio on a 100-vertex MaxCut instance using a digital quantum processor. This achievement represents a significant step towards realising practical quantum solutions for large-scale combinatorial optimisation.
Depth-Independent QAOA Ansatz for Scalability
A novel approach to quantum computation tackles the challenge of solving complex optimization problems with increasing scale. This method constructs a quantum state by sequentially applying parameterized single-qubit rotations and controlled-phase gates, effectively encoding problem-specific information into a linear chain of entangled qubits. This carefully designed entanglement structure bypasses the need for deep circuits, which are vulnerable to noise and decoherence.
The team demonstrates that this ansatz achieves competitive performance on benchmark combinatorial optimization problems, including MaxCut and graph colouring, even with limited circuit depth. Specifically, the ansatz exhibits superior scaling behaviour compared to standard QAOA implementations, maintaining a high success probability for larger problem instances. The researchers also established a connection between the ansatz parameters and the problem’s underlying structure, enabling efficient optimization and improved solution quality.
LC-QAOA Performance on MaxCut Instances
Detailed experimental results demonstrate the performance of a QAOA variant, LC-QAOA, on MaxCut problems. The authors investigated the algorithm’s performance on various MaxCut instances with different graph sizes, degrees, and edge weights. They also explored the impact of post-processing techniques and the length of the chain used in the quantum circuit. The results consistently show that LC-QAOA can achieve good approximation ratios, and certain techniques further improve performance. Tests on graphs with 40, 60, 80, 100, and 120 vertices, all with each vertex connected to three others, show that the mean approximation ratio remains relatively stable across different graph sizes, suggesting the algorithm scales reasonably well.
Further analysis on weighted graphs with varying degrees of connectivity confirms the algorithm’s effectiveness, maintaining consistent performance across different network structures. The application of a post-processing step, known as bit-flip, consistently improves the approximation ratio and, in some cases, identifies the optimal solution. Analysis of the relationship between the chain length and the mean approximation ratio demonstrates that using a longer chain generally improves performance, although the algorithm can still function effectively with shorter chains.
Shallow Circuits Solve Larger MaxCut Problems
Researchers have developed a new approach to QAOA that addresses the challenge of increasing circuit complexity as problem size grows. They designed a linear chain ansatz, a modified quantum circuit structure, that significantly reduces the computational demands for solving combinatorial optimization problems. By arranging entangling gates sequentially along a linear chain within the MaxCut graph, the team achieved a shallow circuit depth independent of problem size, enabling calculations on larger instances. Demonstrations on a digital quantum processor with 100 qubits yielded a mean approximation ratio of 0.
78 for solving MaxCut problems with 100 vertices, representing a state-of-the-art result among QAOA variants. The application of a bit-flip post-processing step improved the approximation ratio to 0. 95 and successfully recovered the true MaxCut solution, demonstrating the potential for enhanced performance through data refinement. While current demonstrations are limited by the number of qubits available, the researchers suggest that quantum advantage may emerge with access to quantum hardware featuring a significantly higher qubit count.