This was a prospective study conducted in the adult intensive care units (ICUs) at a comprehensive cancer center in Amman, Jordan, between June 2019 and May 2022. The center is a 352-bed comprehensive cancer center that includes two medical-surgical ICUs with a total of 21 beds. These ICUs manage both cancer and non-cancer-related critical illnesses in patients receiving medical care at the center.
Eligible patients were adults (≥ 18 years old) who were prescribed vancomycin during their ICU stay, had stable renal function, and were expected to remain in the ICU for the duration of the vancomycin study samples. Stable renal function was defined as serum creatinine that increased by no more than 0.3 mg/dL and urine output that decreased by no more than half over the last 48 h before obtaining the study samples. Exclusion criteria included patients with a do-not-resuscitate or comfort care code status, those on dialysis, and patients admitted to the ICU for post-surgery observation. Informed consent was obtained from the patient or responsible caregiver.
The vancomycin dosing regimen was determined by the clinical team, based on the renal function of the patient and predicted pharmacokinetics. Patients enrolled in the study had one set of three vancomycin concentration levels measured at steady-state: midpoint, peak, and trough. Steady-state was defined as occurring after the patient received at least 3 doses of vancomycin in the ICU. The midpoint concentration was measured at half the dosing interval: for an 8-hour dosing interval, the midpoint sample was taken approximately 4 h after the end of the infusion; for a 12-hour interval, approximately 6 h after the end of the infusion; for a 24-hour dosing interval, approximately 12 h after the end of the infusion. The peak concentration was measured 1 h after the end of the vancomycin infusion, and the trough was measured 30 min before the start of the next infusion. Study samples taken were witnessed by one of the research co-investigators to record the exact timing of the sample. For cases where the exact time was not documented, the sample time for the trough was assumed to be 30 min before the start of the next dose, and that for the peak at 1 h after the end of the infusion, and we referred to the default standard administration times of the institution as a reference point. For the time of the mid-point concentration, it was assumed to be at 4, 6, or 12 h after the end of the infusion, based on the prescribed dosing interval. Patients with vancomycin doses that were given earlier or later than scheduled were not excluded.
To estimate the AUC24 from a single midpoint concentration, we used the following short infusion vancomycin model equation to first estimate k:
-
Maintenance dose in milligrams (MD) = [C_mid (Cl) (tin) (1 – e – kτ)]/[(1 – e –ktin) e – ktmax [12].
-
C_mid (µg/ml) was the vancomycin measured level through k estimation.
-
Cl (L/hr) was the clearance which equals to (k. Vd).
-
k (hr –) was the elimination constant that was derived using an iterative method.
-
Vd (L) was the fixed volume of distribution of 0.7 L/kg, derived from the Thomson model [13].
-
Tin (hr) was the infusion time which was either over 60–90 min depending on the vancomycin prescribed order.
-
τ (hr) was vancomycin dosing frequency.
-
tmax was the time interval between the midpoint level and the end of the previous vancomycin infusion.
This short infusion model was manually created as an equation in Excel to estimate k using an iterative approach. The iterative method is a mathematical technique used to calculate pharmacokinetic parameters [14]. We started with a random initial approximation for the value of k and then repeated by increasing or decreasing the number until the predicted vancomycin concentration closely matched the measured concentration in the patient. After estimating k, we estimated Cl using k * Vd. Then the AUC24 was calculated using the following equation AUC24 = Total daily dose/Cl.
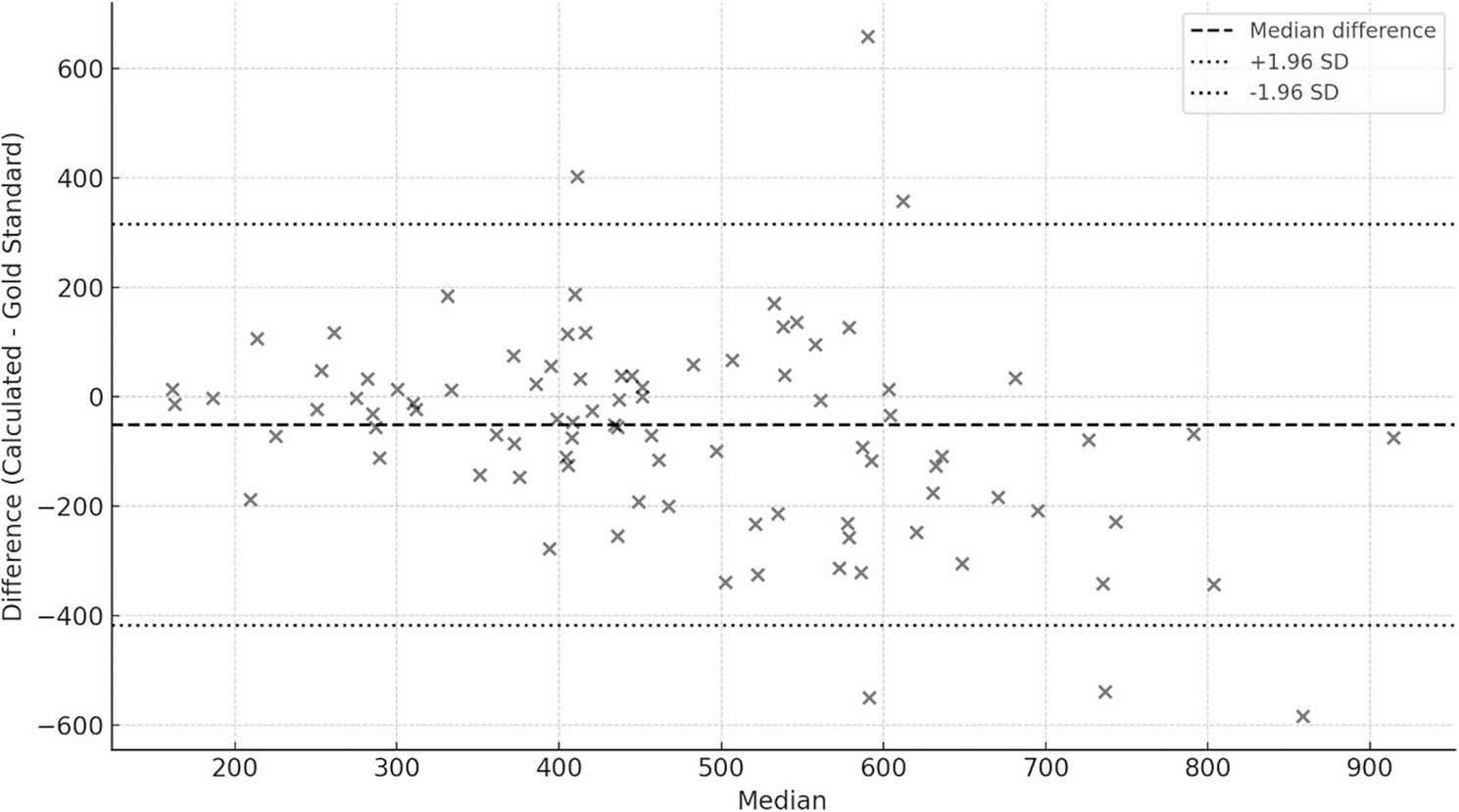
The AUC24 derived from the midpoint concentration was compared to the AUC24, utilizing the guidelines recommended approach, which was considered the gold standard AUC24. The guidelines recommend obtaining two pharmacokinetic samples, a peak taken at 1–2 h post infusion and a trough, obtained at the end of the dosing interval, and utilizing Bayesian software [1, 11]. We used the study peak and trough concentrations obtained at steady-state and the Bayesian software program from InsightRx. The Thomson model [13] and a Vd of 0.7 L/kg were used in the Bayesian analysis to estimate steady-state AUC24 as well as the clearance and volume of distribution. At the time of the study, there were no pharmacokinetic models that were specific for critically ill patients with cancer in the Bayesian software, InsightRx. Therefore, we considered the Thomson to be the most appropriate to use since it reflected the pharmacokinetics of a diverse group of hospitalized patients. Though others have suggested the use of a two-compartment model for vancomycin in critically ill patients [15], we used the Thomson model for the reasons above. Furthermore, although there might be a statistically significant difference between AUCs from one- and two-compartment models, it was reported that the level of difference was acceptable from the clinical perspective [16].
Patient electronic medical records were used to derive the patient demographics and characteristics as well as the laboratory results. The following data was collected: patient demographics, ICU admission diagnosis, requirement of mechanical ventilation, and need for vasopressor support, the number of concomitant nephrotoxic medications, laboratory results, and vancomycin dosing regimens.
Statistical analysis
Categorical data were reported as counts and percentages, and continuous data as means and standard deviations or medians and interquartile ranges (IQRs). Estimating AUC24 using the midpoint was evaluated by determining its accuracy and precision, in reference to the gold standard, two-level Bayesian-based approach. The accuracy was defined as the median % predicted error and was calculated using the following equation: (Xestimated − Xactual)/Xactual*100. Precision was defined as median % predicted absolute error and was calculated using the following equation: (∣Xestimated − Xactual∣)/Xactual*100. The values for the Xestimated were AUC24 derived from one sample mid-point non-Bayesian and the values for Xactual were AUC24 derived from using two samples and Bayesian software. Given that this was a new strategy to estimate non-Bayesian derived AUC24, CL, and Vd, a threshold was not established in this study for accuracy and precision. However, we utilized the boundaries for accuracy and precision that were utilized in previously published reports, which have been < 5 to 20% [17]. The analysis was planned for the entire cohort as well as for subgroups based on the dosing intervals (8-hour, 12-hour, and 24-hour).To determine the impact of the mid-point dosing method on decision making and patient management, we also compared the proportion of AUC24 that are considered therapeutic (i.e., AUC24 ≥ 400, where dose adjustments are not required) in the midpoint and gold standard groups. Bland-Altman plot and a clinical decision agreement table were used to present the comparison of AUC24 between both groups. Python version 3.8 was used to perform the analysis.