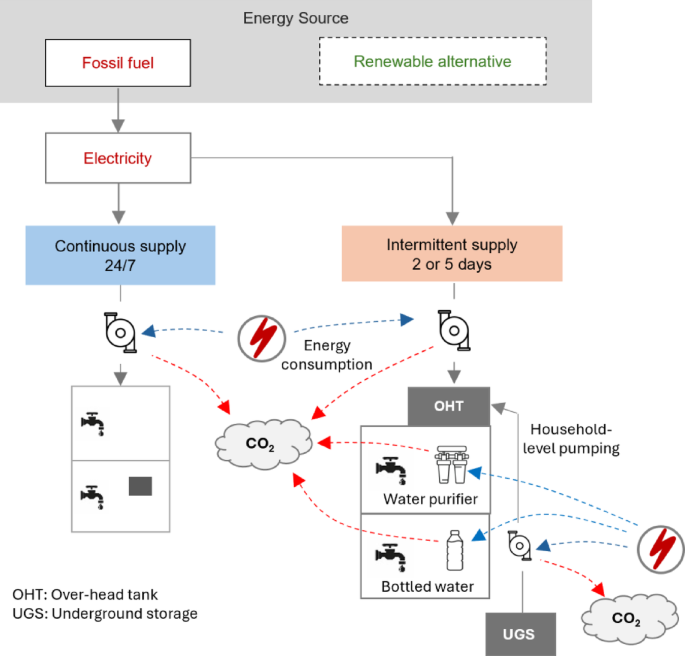
Energy assessment framework
Figure 2 illustrates the proposed framework of WECN in water distribution systems operating with continuous and intermittent supplies in arid regions. The framework comprises a probabilistic energy assessment that considers variations in municipal supply, domestic consumption, pump types, and operating conditions at the household level. First, the required data for two water distribution systems, one operating with continuous and the other with intermittent supplies, was obtained from the National Water Company (NWC). The data for household-level pumps was obtained from the local market. The various probability distributions for water consumption patterns and household pump usage were generated using @Risk Software (8.8.1 Industrial Edition). The study examined variations in metered water consumption in terms of household size. Various scenarios were developed to capture the impact of topographical variations and duration of supply on pumping energy consumption in the selected distribution networks. The study performed both actual and hypothetical baseline scenario analysis, assuming no water loss for the comparative evaluation. Later, the study assessed the impact of water loss on energy consumption in distribution networks for the actual scenarios. Sensitivity analysis using the Monte Carlo method identifies the most significant factors contributing to energy consumption in intermittent and continuous supply systems. Energy and carbon indicators were evaluated based on probabilistic energy analysis for cross-study comparison. Finally, the framework considers a realistic case, taking into account consumers’ concerns about water quality, by assessing the impact of using mineral water bottles and household-level purifiers on the energy and carbon footprint of intermittent water supply. The details of the various framework components are as follows.
Study region, baseline data, and assumptions
Al-Qassim Region is one of the 13 administrative regions in Saudi Arabia, located in the north-central part of the country. The population of 678,000 in the city of Buraydah, the capital of the Qassim area, receives treated groundwater from the municipality24. The Qassim region generally experiences hot summers and cold winters, with limited rainfall during the spring and winter seasons. Figure 3 illustrates the location of the study area in the south of Buraydah, the capital of the Qassim area in the Kingdom of Saudi Arabia. Figure 3 also illustrates the two distribution networks serving Area 1 and Area 2, which were evaluated in the present study. The study area consists of rolling terrain with an average ground elevation of 600 m above sea level. A water treatment plant in Al Shimasiyah, located 35 km away, started supplying the study region in June 2022. The region’s location was selected based on various criteria, including days of supply, diverse topography, and data availability. Figure 3 illustrates the study area, showing the different types of supplies received per week.
WECN assessment framework for distribution systems with continuous and intermittent supplies.
Area 1, spanning over 2.59 km2, serves 379 households with a 2-day intermittent supply, while Area 2, covering 4.94 km2, serves 959 households through a 24/7 continuous supply. Consumers in Area 1 store the supplied water in underground storage tanks and use it for the remainder of the week. The pipe materials are HDPE (high-density polyethylene) and UPVC (unplasticized polyvinyl chloride), with an average age of around 10 years. The ground elevation from mean sea level (MSL) in Area 1 varies between 604 m and 652 m, and between 603 m and 619 m in Area 2. Table 1 presents the characteristics of water distribution systems in the study region. The total length of pipes in A1 is 7,716 m. Approximately 90% of the pipes are made of high-density polyethylene (HDPE) with diameters ranging from 75 to 180 mm, while the remaining 10% are made of unplasticized polyvinyl chloride (UPVC).
Water supply data for September 2023 to February 2024 were obtained from NWC. For energy analysis, the detailed water consumption data per household for February 2024, reflecting the average case, were obtained from the NWC Office in Buraydah, Qassim, KSA. The study assumes an average of 5.6 persons per household, which is the average household size in the KSA25. In the absence of information on per capita consumption variations, the study assumed an average water consumption of 250 L per capita per day (lpcd), as reported for the City of Buraydah by the Ministry of Municipal and Rural Affairs in KSA26. The study also assumed residents consume tap water for drinking in the case of a continuous supply.
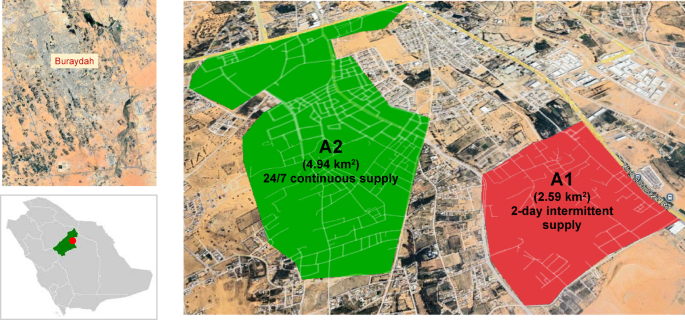
The study region shows three districts with different types of supplies. A1: Khub AlUshar and Elnasryah with 2-days’ supply, A2: Elkhodor with 7- days’ supply.
Water supply scenarios
The distribution network of Area 1 comprises 76 nodes and 85 pipes, serving 379 households. The network in Area 2 contains 282 nodes and 341 pipes, serving 959 households. Figure 4a and b show the hydraulic Models for Area 1 and Area 2. In addition to the actual conditions of a 2-day intermittent supply in Area 1 and a 7-day continuous supply per week in Area 2, six additional scenarios, described in Table 2, were evaluated to capture variations in topography and supply duration.
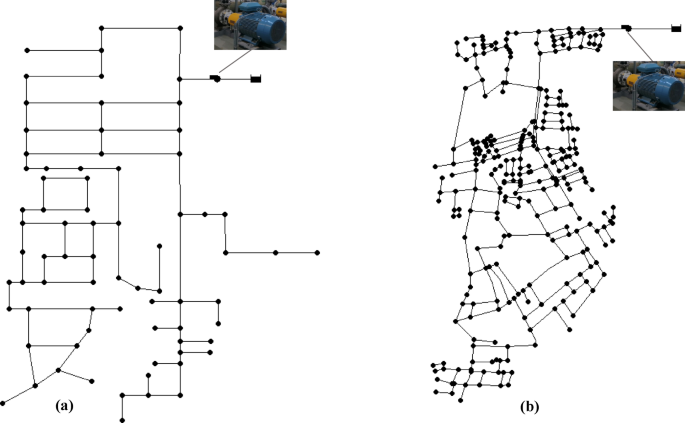
Hydraulic Model for the study region using EPANET 2.0, (a) Area-1 spanning over 259.13 hectares, (b) Area-2 spanning over 494.77 hectares.
Energy Estimation for continuous supply
Water supply systems aim to deliver water to people in an adequate amount at acceptable pressures. Pumping is one of the most critical functions of a water supply system. Pumps are stationary engineering equipment that convert mechanical energy from a revolving shaft into hydraulic pressure27. Common types of pumps used in water distribution systems include centrifugal, vertical, and submersible6. The efficiency curve for larger pumps indicates an increase in energy consumption with increasing flow and head, which typically operates within a desired range, depending on variations in water demand.
The NWC is using centrifugal pumps for supply in the study region. Equation (1) estimated the power consumed by the pumps used for water distribution in the study region28.
$$:{P}_{D}=frac{{Q}_{D}rho:g{H}_{D}}{(3.6times:{10}^{6}){eta:}_{D}}$$
(1)
Where (:{P}_{D}) is pump power (kW), (:{Q}_{D}) is flowrate (m3/h), (:rho:) is density (kg/m³), (:{H}_{D}) is the total pump head (m), (:g) is the acceleration due to gravity (9.81 m/s2), and (:{eta:}_{D}) is the efficiency of the distribution pump (%).
The flow rates for the distribution pumps were estimated for peak-hour demand in scenarios with a 24/7 continuous supply, and for maximum daily demand in scenarios with intermittent supply, considering both pumping and household storage. Based on personal communication with the supplier in the study region, the peak hour factor of 2.25 and the maximum day factor of 1.5 were used as the common values to estimate flow rates from average daily demand.
Equation (2) calculated the distribution system’s pump energy for a continuous supply.
$$:{E}_{CS}={E}_{D}=:{P}_{D}times{t}_{D}$$
(2)
Where (:{E}_{CS}:)represents the pumping energy for continuous supply (kWh), (:{E}_{D}:)represents the pumping energy for water distribution (kWh), and (:{t}_{D}) denotes the pump operating hours (h) of distribution pumps. In the case of a continuous water supply (:{E}_{CS}={E}_{D}.).
Energy Estimation for intermittent supply
A detailed shop-to-shop local market survey was conducted to gather information on the types of pumps used in the study region through personal communication and site visits. Table 3 summarizes the technical specifications for 32 pumps used to lift water from underground tanks to rooftop tanks at the households in the study region. The data show significant variation in the pumps’ flows and heads among different manufacturers, accommodating varying user choices, household sizes, and building heights. Small centrifugal pumps at the household level operate at average efficiencies ranging from 45 to 70%, while submersible pumps operate at slightly higher efficiencies29. The personal communication with professionals involved in installing these pumps revealed that the efficiency of the pumps varies between 50% and 70%, or even higher when they are new. Due to a lack of information (inadequate records of buyers’ addresses and the absence of a disclosure control protocol) regarding sales volume, all the pumps listed in Table 3 were assumed to be used at households in the same proportion.
Local markets provide a variety of sizes for overhead tanks. The Most installed units in residences had a capacity of 3,000 to 4,000 L. In this study, the tank capacity used for calculations was 3,000 L (3 m3), as it is the Most widely used size. The height of the overhead tank is contingent upon building type and the required water pressure. Installing the overhead tank on a support at a minimum distance of 0.5–1 m from the roof slab enhances cleaning and maintenance procedures while safeguarding the structural integrity against damage from water leaks.
Equation (3) estimated the time required to fill the rooftop tank.
$$:text{T}=frac{V}{Q}$$
(3)
Where (:Q) is the flow rate of the pump (m3/min), (:V) is the volume of the rooftop tank (m3), and (:T) is the time to fill the tank (min).
Equation (4) estimates the number of rooftop tanks ((:{N}_{t})) required for domestic consumption per day ((:{Q}_{out})) for each household.
$$:{N}_{t}=frac{{Q}_{out}}{V}$$
(4)
Equation (5) estimated daily pumping time for each household ((:{t}_{H})).
$$:{t}_{H}=frac{V}{Q}times:{N}_{t}$$
(5)
The present study developed a probability distribution for the 32 household pumps presented in Table 3 and used that to estimate the pumping time required for each household. An example of tH estimation is given in Appendix A of the supplementary material.
The total pumping energy for the intermittent water supply system up to the delivery point was estimated using the following Equation:
$$:{E}_{PIWS}={E}_{D}+{E}_{H}=left({P}_{D}times{t}_{D}right)+left({P}_{H}times{t}_{H}right)$$
(6)
Where (:{E}_{PIWS}:)represents the pumping energy consumption for intermittent supply (kWh), (:{E}_{H}) is energy for household pumping, (:{P}_{H}) is the pump power for household pumping (kW), (:{t}_{H}) represents the operating hours (in hours) of household pumps.
$$:{P}_{H}=frac{{Q}_{H}rho:g{H}_{H}}{(3.6times:{10}^{6})eta:}$$
(7)
Where (:{Q}_{H}) is the flow rate of the household pump (m3/h) and (:{H}_{H}) is the head of the household pump (m).
Water-energy-carbon indicators
The water-energy-carbon nexus (WECN) for a water distribution system can be assessed using suitable indicators that are simple to measure, understand, and comparable with the findings of other studies. The denominator of an indicator generally makes it comparable, for example, estimated energy or CO2 emissions per unit volume of water consumed or per population served. Comparing a study’s results for a geographical region with those of other areas identifies overperformance, average performance, or underperformance, which in turn leads to the development of improvement plans.
For an effective comparison, the present study selected “kWh per m3 of metered consumption” (kWh/m3) as the energy indicator, which has been frequently used in several past studies11,30,31,32. The analogous carbon indicator is “kg of CO2 equivalent emissions per m3 of metered consumption” (kg CO2 eq/m3)11,33. Another understandable and comparable carbon indicator is “kg of CO2 equivalent emissions per person per year” (kg CO2 eq/person-year), adopted by Smith et al.34.
Carbon emissions factors are required to calculate the above carbon indicators. The values of these factors primarily depend on the type of energy source, e.g., crude oil, diesel, natural gas, solar, and wind. The carbon emission factor for electricity generation using crude oil ranges from 0.65 to 0.80 kg CO2 per kWh, depending on the specific crude oil type, the technology used for electricity generation, and the combustion efficiency of the process. Studies in KSA also reported a carbon emission factor within the same (0.65–0.8) range35,36,37.
Energy utilized for drinking water with intermittent supply at the user end
A past study identified the recurrence of suspended solids and iron, as well as the complete absence of chlorine (potentially indicating the presence of pathogens), at the consumer end for intermittent supply systems in the study region13. The residents of the study region are well aware of the potential for water quality issues in underground or rooftop tanks due to intermittent supply. A study in Jeddah, KSA, reported that 60% of the samples collected from 36 residential districts were contaminated with coliform bacteria38. Consequently, they use bottled water, generally 20-liter bottles available in local markets, or three-step household-level water purifiers installed at the kitchen tap. The first step in these purifiers is pre-treatment using polypropylene filters (commonly known as sediment filters) to remove sand, silt, or clay that may have entered through cracks in the walls of underground tanks. The second step eliminates organics or chlorine to resolve taste or odour issues by using activated carbon filters. The final step is reverse osmosis (RO), which removes total dissolved solids and pathogens. In some cases, UV sterilization is the fourth step in the disinfection process39.
Assuming a 2-liter per capita daily consumption of mineral water, the average energy consumption for a standard 20-liter bottle of drinking water was found to be 0.108 kWh per person per day. For the water purifier installed at the kitchen tap, the average energy consumption was 0.0425 kWh per person per day. Table 4 presents the step-by-step calculations for both cases.
Therefore, the total energy for the intermittent water supply system up to the consumer end was estimated using Eq. (8):
$$:{E}_{IWS}={E}_{D}+{E}_{H}+{E}_{B}+{E}_{T}$$
(8)
Where (:{E}_{IWS}:)represents the pumping energy consumption for intermittent supply (kWh/person/day), (:{E}_{B}) is energy for bottled water consumption (kWh/person/day), and (:{E}_{T}) represents the energy consumption for household-level water purifiers installed at the kitchen tap (kWh/person/day). The estimated values of (:{E}_{D}) and (:{E}_{H}) were transformed into similar units for comparison.