Majorana zero modes, exotic states of matter with potential applications in advanced computing, continue to fascinate physicists, and recent work by Giulia Venditti, Christophe Berthod, and Louk Rademaker, from the University of Geneva and Leiden University respectively, reveals a surprising new property of these elusive particles. The team demonstrates that Majorana zero modes residing at the cores of vortices can possess a measurable angular momentum, establishing distinct ‘flavours’ of these modes that are independent of previously understood classifications of topological superconductors. Through detailed calculations using microscopic models and advanced computational techniques, the researchers classify the possible numbers of Majorana zero modes based on the behaviour of the superconducting material and the underlying normal state, offering new insights into their topological protection and stability. Importantly, the study highlights limitations to the stability of these modes in specific materials, while simultaneously suggesting that exploring these different ‘flavours’, such as angular momentum, represents a promising avenue for future research into Majorana zero modes.
Topological Superconductivity and Majorana Fermions Overview
This collection represents a comprehensive exploration of topological superconductivity, Majorana fermions, and related phenomena in condensed matter physics. It details the theoretical foundations of topological superconductivity, the emergence of Majorana fermions as unique zero-energy modes, and methods for their detection and characterization. The research builds upon the understanding of topological insulators, materials possessing protected surface states, and investigates how these states interact with superconductivity to create Majorana bound states, particles that are their own antiparticles, holding promise for applications in topological quantum computation due to their unique non-Abelian statistics. The collection also examines the behavior of vortices, topological defects within superconductors, and how they can host Majorana fermions.
Researchers explore vortex core states, localized energy levels within vortices, and techniques for probing their properties through vortex spectroscopy. The study of vortex glass phases, disordered arrangements of vortices, provides further insight into the complex behavior of unconventional superconductors. The research extends to unconventional superconductivity, systems that deviate from standard theories, and the potential for harnessing Majorana fermions as qubits in a topologically protected quantum computer. A central theme is topological protection, the goal of creating systems where Majorana fermions are shielded from environmental disturbances by the material’s topology, crucial for maintaining quantum information.
The research highlights the importance of the proximity effect, coupling topological insulators to conventional superconductors, as a means of inducing superconductivity and creating Majorana fermions. Researchers utilize topological invariants, such as winding numbers and Chern numbers, to characterize materials and predict the existence of topological phases and Majorana fermions. The non-Abelian statistics of Majorana fermions, allowing for unique quantum operations, are explored, alongside their appearance as zero-energy modes at material boundaries. While not a comprehensive materials catalog, the research suggests investigations into materials like bismuth selenide, bismuth telluride, antimony telluride, strontium ruthenate, iron-based superconductors, twisted bilayer graphene, and silicon surfaces. Ultimately, this collection represents the forefront of research in topological superconductivity and Majorana fermions, aiming to discover and characterize materials hosting these states, develop techniques for their manipulation, and build a robust, topologically protected quantum computer.
Majorana Angular Momentum and Topological Superconductors
Researchers have demonstrated that Majorana zero modes, exotic states with potential applications in quantum computing, possess a previously unrecognised property: angular momentum. This discovery establishes new classifications of these modes, extending beyond conventional topological classifications. The team constructed a microscopic model of a superconductor placed on a three-dimensional topological insulator, employing a Dirac model to simulate the material’s electronic structure. The study classified the possible numbers of Majorana zero modes based on the winding of the superconducting order parameter and the underlying normal state, meticulously mapping the relationship between these parameters and the resulting topological properties.
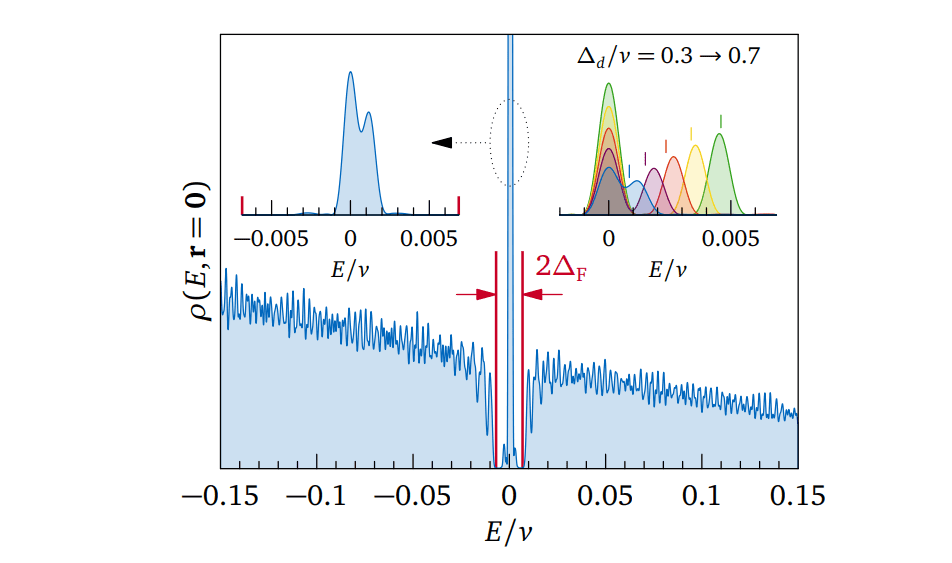
Researchers then examined the topological protection of the Majorana zero modes, considering factors such as the bulk gap and the potential for quasiparticle poisoning, which can limit stability. They used a computational lattice model, verified by a gauge-independent numerical method, to confirm the calculated Chern numbers, a key indicator of topological superconductivity. By establishing a connection between odd Chern numbers and the presence of Majorana zero modes, the team developed a mathematical framework describing how the winding of the superconducting order parameter, combined with a vortex structure, gives rise to topologically protected edge states. This framework, applied to a Bogoliubov-de Gennes Hamiltonian, allowed the team to model the behavior of electrons and holes in the presence of a vortex. By simulating a “puncture” in a topological superconductor on a square lattice, researchers calculated the energy dispersion of edge modes, revealing a linear dependence on angular momentum. This analysis demonstrated that in the absence of a vortex, the angular momentum must be half-integer, while the presence of a vortex allows for an integer angular momentum, including a zero-energy state identified as the Majorana zero mode.
Majorana Zero Modes Exhibit Nontrivial Angular Momentum
Scientists have demonstrated that Majorana zero modes, exotic states with potential applications in quantum computing, carry nontrivial angular momentum, establishing new classifications of these unique states independent of conventional topological classifications. Through analytical calculations and numerical simulations using microscopic models of superconductors on topological insulators, the team successfully calculated the angular momentum carried by these vortex-core Majorana zero modes. The research also highlights limitations to the stability of Majorana zero modes, particularly concerning the influence of the bulk energy gap and the potential for quasiparticle poisoning. Researchers found that the topological protection of Majorana zero modes is limited by these factors, as well as their localization length.
The team investigated the behavior of Majorana modes in a vortex structure, finding that the angular momentum is intricately linked to the winding numbers of the superconductor and the normal state. Specifically, the research shows that the angular momentum of the Majorana modes is determined by the relationship between the winding numbers. Analysis of the radial structure of the Majorana zero mode wavefunction, simplified by assuming a constant order parameter, indicates that the wavefunction components are proportional to Bessel functions, and the Majorana mode exhibits maximum probability at the vortex center only when specific conditions are met. This condition ensures the wavefunction remains single-valued and avoids vanishing intensity at the vortex core. The team’s findings, supported by lattice simulations, demonstrate that the Majorana zero mode’s localization and intensity are critically dependent on the winding numbers and the interplay between the superconductor and the topological insulator.
Majorana Zero Modes Exhibit Angular Momentum
Scientists have demonstrated that Majorana zero modes, exotic states with potential applications in quantum computing, can possess a previously unrecognised property: angular momentum. This research establishes distinct ‘flavors’ of these Majorana modes, extending beyond classifications based on the topological properties of the superconducting materials that host them. Through both analytical calculations and numerical simulations using microscopic models of superconductors on topological insulators, the team successfully calculated the angular momentum carried by these vortex-core Majorana zero modes. The investigation classified the possible numbers of Majorana zero modes based on the way the superconducting order parameter winds around the vortex core.