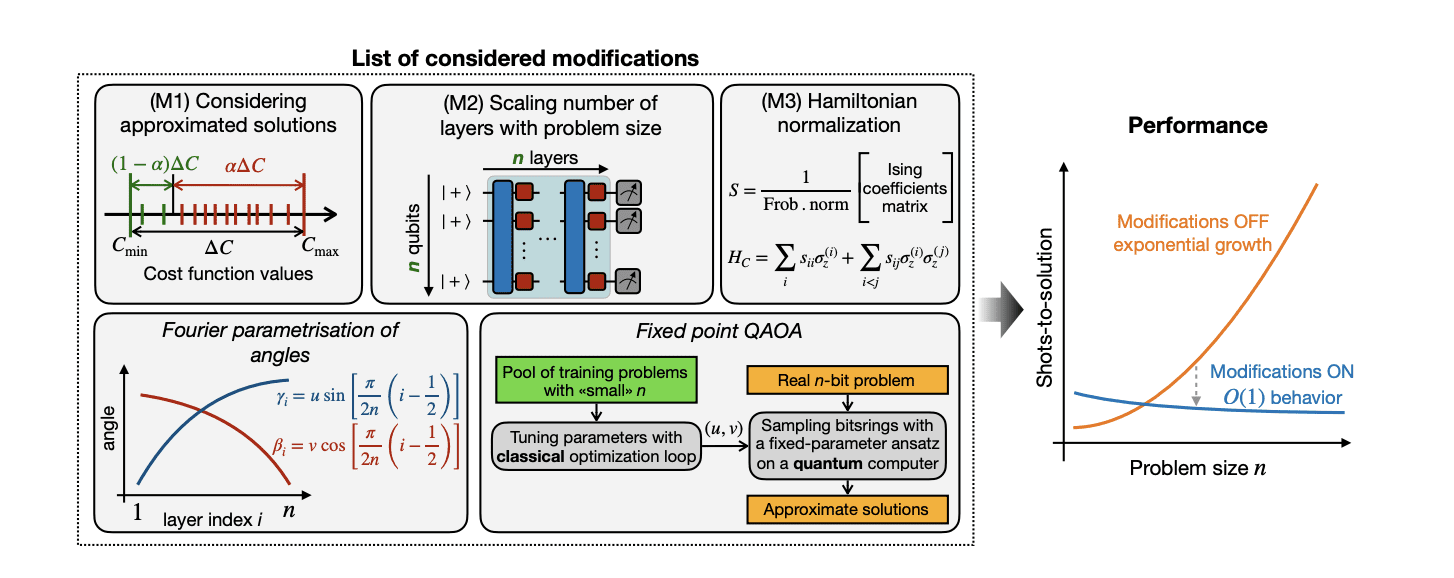
Quadratic unconstrained binary optimization (QUBO) problems underpin many real-world applications, and the Quantum Approximate Optimization Algorithm (QAOA) offers a promising quantum route to finding solutions. However, practical implementations of QAOA often struggle with noise and computational challenges. A team led by A. Yu. Chernyavskiy, D. A. Kulikov, and B. I. Bantysh, alongside Yu. I. Bogdanov, A. K. Fedorov, and E. O. Kiktenko, all working to advance quantum computation, now presents a modified version of a fixed-parameter QAOA scheme that dramatically improves its efficiency. Their work demonstrates that by focusing on achieving a target level of accuracy rather than the absolute optimum, carefully scaling problem parameters, and employing a specific circuit structure, the algorithm requires a consistently low number of computational steps, regardless of problem size. This achievement, which suggests a solution complexity independent of problem size, represents a significant step towards building practical and scalable quantum optimisation algorithms.
This work builds upon existing QAOA methodologies, aiming to overcome limitations in scalability and efficiency when addressing complex optimisation challenges. The team’s work demonstrates that a carefully designed approach can significantly improve QAOA’s efficiency. Numerical experiments confirm that a modified approach, fpQAOA, demonstrates better scaling than traditional implementations. A critical finding is the importance of problem scaling, specifically how the QUBO problem is prepared before being processed by QAOA. Different scaling strategies, including max-abs, weighted norm, and the team’s chosen Frobenius norm, dramatically impact performance, with the Frobenius norm consistently outperforming the others.
The team also demonstrates that optimising parameters based on achieving a specific approximation ratio is more effective than directly optimising the full approximation ratio expectation. A key observation is that their approach leads to a non-increasing number of quantum circuit runs, known as Shots to Solution, as the problem size increases, indicating that the algorithm’s performance does not degrade with scale. Optimising for a specific approximation ratio, such as 0. Scientists developed a modified fixed-point QAOA scheme that combines focusing on the probability of achieving a target approximation ratio, setting the number of layers equal to the problem size with a specific angle encoding, and rescaling problem coefficient matrices. Extensive numerical studies across diverse quadratic unconstrained binary optimization problems, ranging in size from 5 to 24 variables, demonstrate that this combination leads to a remarkable result: the median number of shots required to find approximate solutions does not increase as the problem size grows, effectively achieving a constant-shot complexity and a substantial improvement over existing methods. Importantly, the researchers demonstrated that omitting any single component of their approach restores the exponential scaling typically associated with current quantum heuristics. The team acknowledges that their conclusions are based on statistical evidence derived from median and percentile metrics, rather than strict analytical guarantees, establishing a strong empirical basis for constant-shot scaling and providing a promising pathway for overcoming bottlenecks in the implementation and scalability of QAOA.