Quantum electrodynamics, the theory describing how light and matter interact, presents significant challenges when simulating systems with a non-zero density of particles, a condition found in many astrophysical environments. Emil Otis Rosanowski, Arianna Crippa, and Lena Funcke from the University of Bonn, alongside Paulo Vitor Itaborai and Karl Jansen from The Cyprus Institute, and Simran Singh from the University of Bonn, now demonstrate a novel approach to tackling this problem using quantum computers. Their work represents a crucial step towards simulating realistic, dense quantum systems, as they successfully implement a method that incorporates fundamental physical constraints directly into the quantum computation. By benchmarking their technique on a small system, the team identifies key phase transitions, paving the way for future investigations into the behaviour of matter under extreme conditions and offering a promising pathway to overcome limitations in classical simulations.
Validating Quantum Simulations of U(1) Gauge Theory
Scientists rigorously tested and refined methods for simulating a simplified version of quantum electrodynamics (QED) using quantum computers. This work focuses on validating the accuracy of these simulations, extending the results to more complex scenarios, and exploring limitations. Researchers combine classical computation with quantum hardware to investigate the behavior of fundamental particles interacting with a force field. The simulations closely match the behavior of the full, unapproximated theory, even with approximations to reduce computational demands, justifying the use of these techniques.
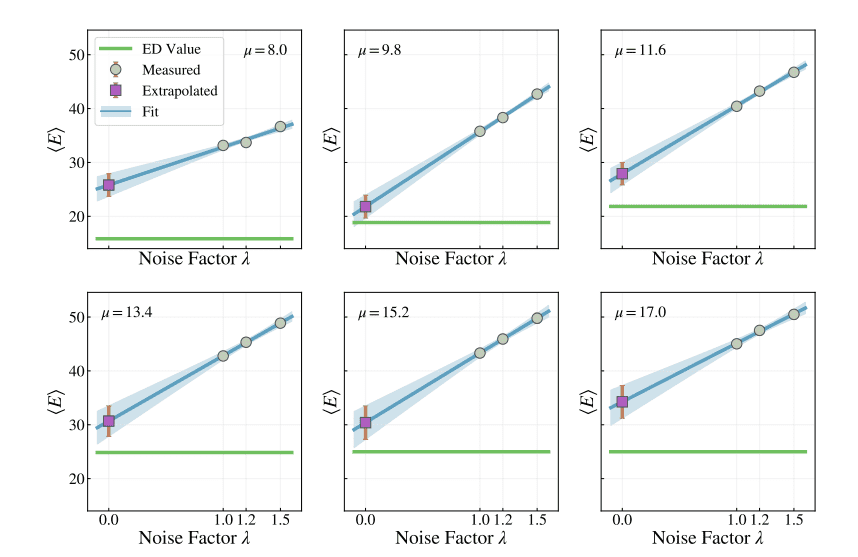
The team extended the simulation to include three types of fundamental particles, revealing five distinct phases characterized by different particle distributions, consistent with theoretical predictions. To address the inherent noise in quantum computers, the team employed zero-noise extrapolation. This method involves running the quantum simulation with varying levels of artificial noise and then extrapolating the results to a zero-noise limit, effectively reducing errors and improving accuracy. This approach proves effective in mitigating the impact of noise and obtaining more reliable results, paving the way for more complex simulations in the future.
Finite Density QED Simulation with Variational Circuits
Researchers pioneered a new method for simulating quantum electrodynamics (QED) at finite density, a condition where the number of particles is not fixed, using a quantum computer. They employed a variational quantum eigensolver, a resource-efficient technique well-suited for current quantum hardware, to explore this complex system. The team developed a quantum circuit that enforces Gauss’s law, a fundamental principle of electromagnetism, ensuring the accuracy of the simulation and allowing for the investigation of finite density with two types of fundamental particles. The team first optimized the quantum circuit using classical simulations before running it on IBM quantum hardware, allowing for benchmarking the finite-density state preparation protocol on small systems. By constructing a mathematical description of the system and mapping it onto the quantum computer, researchers investigate phase transitions by observing the particle number of the fundamental particles, representing a significant step toward simulating real-time dynamics in finite-density systems.
Finite Density QED Simulation via Quantum Computing
Scientists are developing a new approach to simulating quantum electrodynamics (QED) at finite density, a challenging problem in theoretical physics. Their work focuses on a (2+1)-dimensional system with two types of fundamental particles, employing a variational quantum eigensolver protocol to identify phase transitions within the system by analyzing the particle number of the fundamental particles. The core of their method involves constructing a specialized quantum circuit that enforces Gauss’s law, a fundamental principle governing the behavior of charged particles, and restricting calculations to a specific subspace to significantly reduce computational complexity. Experiments demonstrate the ability to accurately determine the locations of phase transitions by analyzing the difference in particle number between the two types of fundamental particles. Further theoretical work establishes a precise formula for predicting the critical conditions at which these phase transitions occur, relating the critical conditions to the ground-state energy of the system.
Fermion Flavors Simulate Electrodynamics at Finite Density
Researchers successfully demonstrated the first quantum simulation of (2+1)-dimensional electrodynamics with multiple types of fundamental particles at finite density. By developing a variational quantum eigensolver protocol, they directly enforced Gauss’s law within the quantum circuit, ensuring the accuracy of the simulation. The simulations reveal evidence of phase transitions, identified through changes in the particle number as the chemical potential is varied, and distinguish three distinct regions based on these changes. While analytical predictions for the precise conditions of these phase transitions are currently unavailable, this work establishes a proof-of-principle demonstration using a relatively small system. The researchers verified their quantum simulations against classical calculations, confirming the feasibility of capturing essential features of phase transitions even on limited systems, and acknowledge that current limitations in circuit depth and hardware noise contribute to some discrepancies in their results.