Surrogate-assisted optimization of roll-to-roll slot die coating

Thin films with a high technical specification have many applications, including within lithium-ion batteries^1,2, solar panels³ and polymer electrolyte membrane fuel cells^4,5. Roll-to-roll slot die coating is a widely used technology for the industrial scale manufacture of thin films, which involves pumping a fluid through a slot in a metal block onto a moving substrate^4,6. The high line speed, high material utilization and ability to pre-select coating thickness are factors which have contributed to roll-to-roll slot die coating becoming ubiquitous in state-of-the-art thin film manufacture⁷.

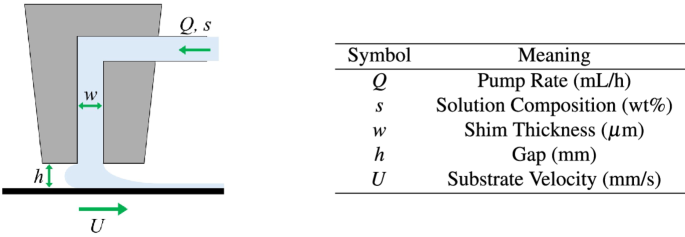
Slot die coating has many adjustable process parameters, which influence the coating formed. These parameters, as illustrated in Fig. 1, include substrate velocity, coating gap, shim thickness and composition of coating solution^4,8. Slot die coating forms defect-free coatings using parameter sets within the operating window⁴. Outside of this window, the coating process is susceptible to significant defects such as ribbing, dripping and air entrapment. However, even when remaining within the operating window, different sets of coating parameters give different coating properties^9,10. The wet coating thickness, for example, can vary within the operating window depending on the ratio of pump rate to substrate velocity⁴. However, more subtle features such as coating uniformity and edge quality also depend on the process conditions used^10,11. Schmitt et al. termed regions within the operating window with a high coating uniformity, the quality window¹⁰.

Many theoretical models can predict the operating window for slot die coating such as those by Ruschak¹², Higgins and Scriven¹³ and Yamamura¹⁴. However, to the best of the authors’ knowledge, there is no efficient theoretical understanding or analytical models, of how process parameters affect features of the coating within the operating window. This is noteworthy as coating properties such as unexpected coating thickness deviations and coating uniformity have a large influence on the performance of subsequent devices¹⁵. For example, a high coating uniformity is essential for Li-ion battery electrodes as it minimizes rejection rate and has a large influence on the electrochemical performance of the electrode^1,16. As a specific example of this, Mohanty et al. found that non-uniform Li-ion NMC electrode coatings gave poor rate capability, especially at higher rates, and a lower Coulombic efficiency¹⁷. Coating uniformity is also an important coating feature for organic photovoltaic devices, with a higher uniformity resulting in improved device performance¹⁸.

Despite the dogma that slot die coating provides perfect thickness control, in reality small changes in the coating width can occur depending on the process parameters used, which in turn alters the coating thickness¹⁹. This effect is due to the non-Newtonian behavior of polymeric coating solutions²⁰. The coating’s thickness determines the energy density of a Li-ion battery, with a thinner than expected electrode giving a lower cell energy density²¹. Additionally, a thicker than expected electrode may lead to mass transport limiting charging/discharging rates. These differences in coating thickness are particularly significant for industrial operators in applications which utilize stripe coatings or with strict thickness requirements.

The lack of theoretical modeling and understanding of how input parameters impact these fundamental coating properties in slot die coating⁴ means that operators currently optimize production through iterative, trial and error adjustments^1,11. The large amount of process parameters and competing outputs exacerbate the complexity of this optimization and make trial and error unlikely to result in the coating process being truly optimized. This has cost implications, due to the waste material produced and production time lost during this laborious process. Additionally, this type of optimization leaves potential device performance improvements untapped.

Despite computer aided optimization having been implemented in a wide variety of manufacturing processes in other sectors, such as additive manufacturing^22,23 and pharmaceutical manufacturing²⁴, it is not routinely applied in industrial roll-to-roll slot die coating lines. Harnessing computer-aided optimization in this context could unlock significant cost and performance benefits for a wide range of devices. Furthermore, such an approach has the potential to provide valuable insights into the relationship between key coating parameters and the resultant properties of the coating.

The literature has documented some instances of computer-assisted optimization for roll-to-roll slot die coating^16,25,26. However, there are no reports linking fundamental process parameters to critical coating properties, highlighting a significant gap in the understanding of slot die coating within its operating window. Additionally, there has not been any utilization of a machine learning model to provide experimental improvements in coating features. This disconnect highlights a divide between the theoretical modeling and practical application, raising concerns about the effectiveness or applicability of the previously reported methods.

Machine learning-based surrogate optimization is well-suited for slot die coating, due to the process’s complexity and the numerous interacting inputs and outputs. Surrogate modeling involves constructing computationally efficient approximations of approximate complex, computationally expensive, or time-intensive simulations using experimental data and is well known for capturing intricate non-linear relationships^16,27. Surrogate models are particularly effective when analytical models are unavailable.

There are a range of analytical approaches and multivariate modeling tools that can be used for modeling industrial processes. For instance, multiple linear regression (MLR), polynomial regression (PR)²⁸, principal component analysis (PCA), latent variable model (LVM), orthogonal partial least squares (OPLS)²⁹, Gaussian process (GP), and Artificial Neural Networks (ANN)³⁰. Among these, Radial Basis Function Neural Networks (RBFNNs), are a notable machine learning modeling method due to their ability to accurately describe complex nonlinear relationships while maintaining computational efficiency. With its universal approximation capability³¹, RBFNNs excel at modeling complex systems with high accuracy and efficiently capturing local variations in data.

However, alternative surrogate modelling methodologies also warrant consideration. For example, Gaussian Process regression is widely recognized for its flexibility and ability to provide uncertainty estimates, making it a strong candidate for problems where quantifying prediction confidence is important. Similarly, Support Vector Regression, which adapts support vector machine methodology to regression tasks, is known for its robustness in high-dimensional spaces and often achieves good generalization on relatively small datasets³². Comparative studies have demonstrated that while RBFNNs typically offer fast training and effective local modelling, Gaussian Process models may outperform them in terms of predictive error under certain circumstances, particularly with small datasets or when uncertainty quantification is required. Furthermore, recent research has shown that SVR can deliver competitive performance, though its accuracy might be surpassed by RBFNNs and Gaussian Process models under some conditions, such as in delamination detection in composite laminates³³. Therefore, incorporating comparative analysis with these surrogate modelling techniques can further reinforce the strengths and appropriate use-cases for RBFNNs, highlighting the need for model selection based on the specific characteristics of the data and the modelling objectives.

Although gradient-based optimization techniques can effectively explore solution spaces, they have inherent limitations such as generalization challenges and a lack of performance guarantees. Surrogate-assisted evolutionary computation addresses these issues by using computationally efficient models to estimate fitness functions in evolutionary algorithms. This approach is particularly valuable for complex optimization problems with computationally expensive objective functions. By employing surrogate models like RBFNNs, this approach significantly reduces the need for costly experimental evaluations, accelerating both exploration and exploitation of the parameter space. Additionally, acquisition functions further balance exploration and exploitation, making this method particularly effective for high-dimensional optimization tasks.

Reference Vector Guided Evolutionary Algorithm (RVEA), a flexible and scalable meta-heuristic evolutionary optimization method³⁴, is well-suited for complex processes, that traditional multi-objective problem algorithms struggle with in terms of performance and diversity maintenance³⁵. RVEA utilizes a uniform distribution of reference vectors – directions in the input parameter space- to guide the search for optimal solutions. This method ensures a diverse set of solutions spread across the Pareto front, which represents the set of optimal trade-offs between conflicting objectives. Additionally, RVEA’s adaptive angle penalty mechanism dynamically adjusts selection pressure, maintaining a balance between convergence and diversity, making it well-suited for complex, high dimensional problems.

This article presents an experimentally validated optimization approach for roll-to-roll slot die coating, combining a RBFNN surrogate model with RVEA. The coating composition used resembles many industrially relevant coatings, such as slurries for lithium ion batteries and solar cells^1,36, making insights gained applicable across a wide range of fields. This article aims to promote the widespread implementation of machine learning-based optimization in roll-to-roll slot die coating, offering potential improvements in cost, performance and process understanding.