Problem statement
Despite its privacy-preserving design, the Beacon protocol is vulnerable to membership inference attacks that can reveal whether an individual is part of a dataset, potentially compromising sensitive information. Existing defenses [4, 7, 12, 18], aim to mitigate these risks but often assume static or batch-query environments. Additionally, current game-theoretic approaches [12, 18] model the problem as a Bayesian game which provides a single perturbation-based solution for all users, leading to sub-optimal privacy protection. In reality, attackers can adapt their strategies in sequential-query settings, making these defenses less effective. Hence, we focus on the problem of designing defenses for evolving and more sophisticated attacks.
The system and threat model
The beacon system responds to received queries on the presence of alleles in the connected database(s) and return ’yes’ or ’no’ response for each dataset. Without losing generality, we assume the beacon is connected to a single database. The protocol operates in an authenticated online setting. That is the querier logs in before posing potentially multiple queries. The system has access to previous queries made by the same querier. This continuous access enables the protocol to accumulate information over time, improving its effectiveness in detecting membership inference attacks. In this context, the beacon assigns probabilities to “yes” responses, reflecting the honesty rate of the system. On the other hand, the honesty rate for “no” responses is always set to one, as research has demonstrated that altering “no” responses to “yes” does not enhance privacy protection for individuals within the system [10]. Note that the beacon publicly shares the honesty rate associated with every answer in our setting, which assumes a very strong adversary. If the querier repeats a previously posed query, the same response is returned, ensuring consistency.
We consider a passive adversary who has access to an individual’s genome and seeks to perform a likelihood ratio test (LRT)-based membership inference attack. The adversary aims to conduct a hypothesis test to confidently determine whether the target individual’s genomic data is included in the dataset accessible via the beacon protocol. We assume the adversary can submit multiple queries without any auxiliary information and that the queries and corresponding responses are independent of each other, i.e., not in linkage disequilibrium. Additionally, we assume the adversary has access to the genomes of a control group of individuals with similar genetic backgrounds to individuals in the beacon dataset, denoted as C.
Similar to many membership inference attacks in the literature [3,4,5, 10], we employ a LRT-based attack. The genome of an individual i can be represented as a binary vector, (varvec{d}_{varvec{i}} = {d_{i1}, . . . ,d_{ij}, . . . ,d_{im}}) where (d_{ij}) denotes the presence of SNP j (1 for “yes”, 0 for “no”) and m denotes the number of known SNPs. The beacon, after receiving a query set, Q consisting (k) queries, generates a binary response set (varvec{x}) where (x_j) denotes the presence of the SNP in the beacon for the (j^{th}) query in Q ((Q_j)).
Assuming that the MAFs for the SNPs are public, the optimal attacker constructs a list Q which contains the SNPs of the victim. It is sorted in ascending MAF order. Let the null hypothesis ((H_0)) refer to the case in which the queried genome is not in the Beacon and the alternative ((H_1)) is otherwise.
$$begin{aligned} L_{H_0}(Q,varvec{x}) = sum limits _{j in Q} left[ x_j log (1 – D_n^j) + (1 – x_j) log (D_n^j) right] end{aligned}$$
(1)
$$begin{aligned} L_{H_1}(Q,varvec{x}) = sum limits _{j in Q} left[ x_j log (1 – delta D_{n-1}^j) + (1 – x_j) log (delta D_{n-1}^j) right] end{aligned}$$
(2)
where (delta) represents the probability of sequencing error, (D_n^i) is the probability that none of the n individuals in the beacon having the allele at position j and (D_{n-1}^j) represents the probability of no individual except for the queried person having the allele at position j. (D_{n-1}^j) and (D_n^j) are defined as follows: (D_{n-1}^j = (1 – f_j)^{2n-2}) and (D_n^i = (1 – f_i)^{2n}), where (f_j) represents the MAF of the SNP at position j. Then, the LRT statistic for person i in the beacon is determined as Eq. 3.
$$begin{aligned} L_i(Q,varvec{x}) = sum limits _{j in Q} d_{ij} left( x_j log frac{1 – D_n^j}{1 – delta D_{n-1}^j} + (1 – x_j) log frac{D_n^j}{delta D_{n-1}^j} right) end{aligned}$$
(3)
While Raisaro et al. (2017) assume that the beacon is honest with all answers, Venkatesaramani et al. (2023) incorporate the fact that the beacon might be lying in the formulation. They introduce a binary variable (y_j) to indicate if the response for the (j^{th}) query was flipped. They consider (Q_1) as the subset of (Q) with (x_j = 1) and (Q_0) as the subset with (x_j = 0). Let (A_j = log frac{1 – D_n^j}{1 – delta D_{n-1}^j}) and (B_j = log frac{D_n^j}{delta D_{n-1}^j}). Thus, by defining (h_j) as the complement of (y_j), representing honesty, the LRT function can be rewritten as in Eq. 4.
$$begin{aligned} L_i(Q, varvec{x}, varvec{h}) = sum limits _{j in Q_1} d_{ij}(h_j A_j + (1 – h_j) B_j) + sum limits _{j in Q_0} d_{ij}B_j end{aligned}$$
(4)
We use Eq. 4 but relax the assumption that (varvec{h}) is a binary vector. We define (varvec{h}) as ({h_jin mathbb {R}:0 le h_j le 1)} where (h_j = 1) indicates an honest response and if (x_j = 0), then (h_j = 1). Thus, the beacon can incorporate uncertainty into the responses and fine-tune the honesty level as desired.
The adversary can decide if the individual (i) is a member of the dataset when (L_i(Q, varvec{x}, varvec{h})) falls below a predefined fixed threshold (theta) [7, 19]. The attacker simulates the attack on the control group C and picks the one that balances precision and recall. However, fixed thresholding can be bypassed using various defense mechanisms [10]. We rather adopt adaptive thresholding, which is a more effective and realistic technique that can work in an online setting and can adjust the threshold (theta) based on the response set (varvec{x}) to the queries Q: (theta (Q,varvec{x})). It ensures the false positive rate for an attack does not exceed a predefined rate [10].
Background on game theory and reinforcement learning (RL)
A Bayesian game is a game with simultaneous moves/actions where players have incomplete information about each other. An (alpha)-Bayesian game is an extension where instead of having precise probabilistic beliefs, players work with a set of possible probability distributions. The parameter (alpha) reflects the players’ level of ambiguity aversion. Stackelberg games, on the other hand, involve a leader-follower structure, where the leader moves first and the follower responds. The leader’s strategy accounts for the fact that the follower will optimize their response after observing the leader’s move. RL has been used to model Stackelberg games in various domains [20,21,22]. RL enables both the leader and follower to learn and adjust their strategies dynamically in real time. It is very effective in games with large actions or state spaces because it can approximate optimal strategies without exhaustively exploring all possibilities.
RL techniques rely on Markov Decision Processes (MDPs), including the following fundamental components: State s represents the state of the world; Action space A is the set of all valid actions available to a player in a given environment; Reward R function computes the reward for a specific state and action, and sometimes it also depends on the next state; Policy (pi) is a rule used by an agent to decide what actions to take by mapping the states of the environment to actions. The environment conveys the current state to the agent and changes with respect to the agent’s actions by transitioning to a new state. It provides a reward or penalty; Value Function V estimates how good a state is, and (Q^{pi }) estimates how good a state-action pair is in terms of long-term rewards. The difference is the advantage (hat{A}); Discount Factor (gamma in [0,1]) weighs how much future rewards are valued compared to immediate rewards.
Privacy and utility definitions
We define the function (p_i) to measure the privacy risk of an individual (i). This function compares the log-likelihood ratio test (LRT) value of individual (i) with the LRT values of all individuals in a control group. It then calculates the percentage of control group members whose LRT values are greater than that of individual (i). It is defined as (p_i(Q, varvec{x}, varvec{h}, C) = [ sum nolimits _{t in C} textbf{1}_{L_i(Q, varvec{x}, varvec{h}) le L_t(Q, varvec{x}, varvec{h})} ] / |C|) where (L) represents the LRT, computed based on the attacker’s set of queries (Q) and sharer’s responses (varvec{x}) as previously described. This function allows us to quantify the risk of re-identification over time as more queries are posed: A lower, rapidly decreasing value is interpreted as high risk, indicating that the probability of correctly re-identifying an individual is increasing.
We quantify the utility of the beacon service using function (u(Q,varvec{h}) = [sum nolimits _{j in Q} (h_j)] / |Q|). The function returns the average honesty level of the responses provided by the system which is captured by the variable (varvec{h}) in the (LRT) function defined in Eq. 4 where (h_j) represents the honesty level for the (j^{th}) query in query set (Q).
Our novel defense strategies
Here, we present a novel game theory-based defense mechanism against LRT-based attacks which can handle a few queries due to the large strategy space. Then, we present the first reinforcement learning (RL)-based solutions.
Stackelberg defender
The interaction between the beacon and the attacker is modeled as a Stackelberg game in which the leader moves first (attacker), and the other player (the beacon) moves subsequently, making decisions based on the leader’s query. The attacker’s strategy in our game is represented by Q where (Q_j) represents the index of (j^{th}) queried SNP where (1 le j le kle m). Unlike in the previous attacks, the attacker can query SNPs not carried by the victim to confuse the beacon service. (varvec{Q} = [Q_1, Q_2, dots , Q_{k}], quad Q_j in {1, 2, dots , m}, quad 1 le j le kle m).
The beacon’s strategy in the game is represented by the vector (varvec{h}) where ({h}_j in [0,1]) for the query j which indicates the honesty rate. We discretize (varvec{h}) for this game and let the beacon choose from four available strategies. The granularity can be increased at the cost of computational time. (varvec{h} = [h_1, h_2, dots , h_{k}], quad h_j in {0.25, 0.5, 0.75, 1}, quad 1 le j le kle m).
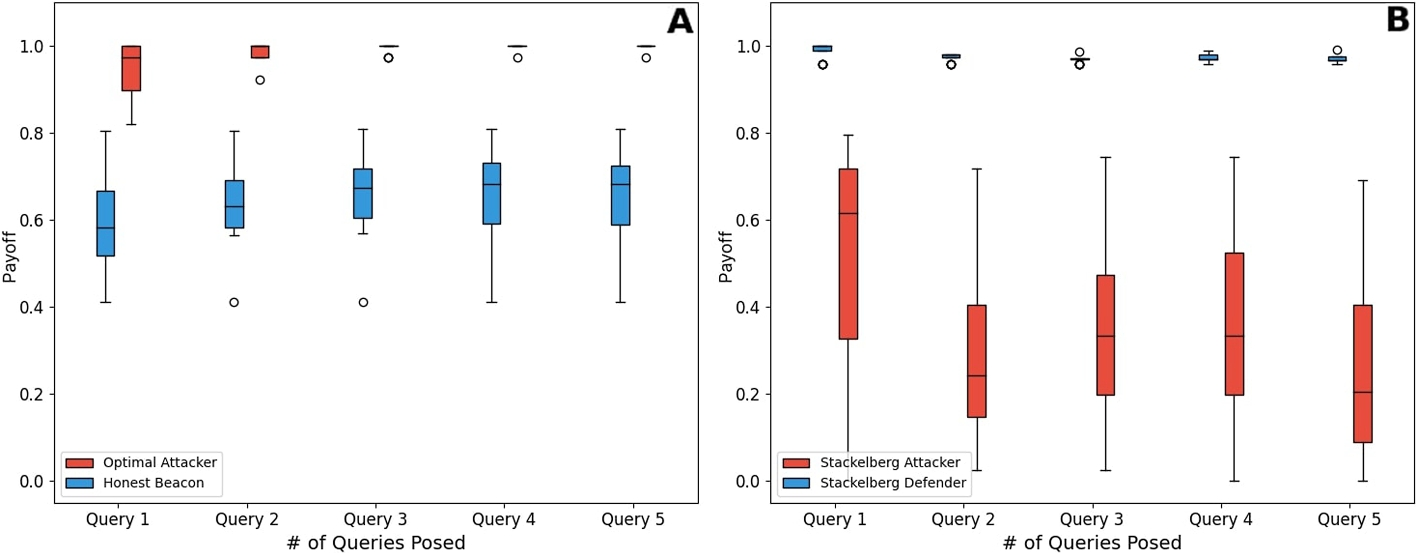
To formulate the problem as a Stackelberg game, we use representations of the attacker and defender utility function, naming payoff function. We define the payoff function of the Stackelberg attacker as (1 – p_{victim}(Q, {textbf {x}}, {textbf {h}}, C)) which is the complement of the victim’s privacy. The payoff function of the Stackelberg defender consists of two parts: (i) a privacy term and (ii) a honesty term. The privacy term first computes the LRT values of the individuals in the control group C for the (i^{th}) query using strategy (h_i). Then, we compute the variance in the first quartile of these values to quantify the risk of privacy violation. High variance indicates that an incoming query is posing a re-identification risk. The honesty term is simply (h_i). The final term is the weighted sum of these two terms, where the weights are hyperparameters to the algorithm. Please see Additional file 1: Supplementary Note S1 for the details about the Stackelberg defender’s payoff calculation.
Reinforcement learning-based attackers and defenders
In this section, we discuss our Reinforcement Learning (RL) approach designed to protect individuals’ privacy in the beacon database while preserving system utility. The environment has two main players: the user (regular or attacker) and the beacon service.
States
The beacon agent’s state space (S_b) consists of the user’s (t^{th}) query (Q_t) and the beacon service’s statistical data at time t. We define (varvec{s}_{varvec{b}}) as the beacon state, where (varvec{s}_{varvec{b}} in S_b). Specifically, each state includes (i) the MAF of the queried SNP j, (ii) the minimum and mean LRT (L_i(Q,varvec{x,h})) values among the individuals in each of beacon database and control group before responding the current query, (iii) potential LRT change by lying or not for SNP j, (iv) the minimum (p_i(Q,varvec{x,h},C)) among beacon participants after lying or not, and finally, (v) the beacon’s utility (u(Q,varvec{h})) up to the current query (Q_t). Importantly, the agent only observes summary statistics rather than individual genomes which reduces state complexity and enhances privacy, especially in decentralized or outsourced training scenarios.
The attacker’s state space (S_a) contains information about the victim. The state (varvec{s}_{varvec{a}} in S_a) categorizes the victim’s SNPs into g groups: (g-1) groups based on their MAF values and another group for SNPs that she does not have. Let (s_{min}) and (s_{max}) be the SNPs with the lowest and the highest MAFs in the group, respectively, For each group, (varvec{s}_{varvec{a}}) includes: (i) (L_{victim}(Q_{s_{min}}, x={0}, h={1})), (ii) (L_{victim}(Q_{s_{min}}, x={1}, h={1})), (iii) (L_{victim}(Q_{s_{max}}, x={0}, h={1})), and (iv) (L_{victim}(Q_{s_{max}}, x={1}, h={1})). The attacker assumes the beacon is honest and calculates the LRT ranges for the rarest and most common SNP in each group as if those were the only queried SNPs. (varvec{s}_{varvec{a}}) also contains (i) the number of SNPs, (ii) the minimum and mean LRT values obtained on the control group C at time t, and (iii) (p_{victim}(Q,varvec{x,h},C)) at time t.
Actions
The beacon agent’s continuous action space (A_b) is an honesty rate to choose for the query j. That is, (A_b = left{ varvec{h} in mathbb {R}^k mid 0 le h_t le 1, , forall t in {1, 2, dots , m} right}). The attacker’s action space (A_a) is a SNP group to choose from: (A_a = left{ varvec{a} in mathbb {Z}^k mid 1 le a_t le g, , forall t in {1, 2, dots , m} right}). From the chosen group, a specific query is then randomly selected for querying.
Rewards
We use both intermediate and final rewards to train our agents. The intermediate reward (r_t) is computed as a function R of a given state-action pair at time t: (r_t = R(varvec{s}_t, h_t)). The function (R_b) assesses the trade-off between privacy and utility for the beacon agent for each query: (R_b = p_{victim}(Q, varvec{x}, h, C) + h_t). As articulated, (p_{victim}) represents the privacy of the victim component, and (h_t) represents the utility of the system for (t^{th}) query. This ensures that each action taken by the beacon considers privacy and utility. For the attacker agent, the intermediate reward function (R_a) is defined based on the beacon’s honesty rate for the (t^{th}) query: (R_a = h_t). Here, the attacker’s goal is to maximize the honesty rate from the beacon’s answers to improve the chances of reidentifying the victim.
In the real-world scenario, the beacon does not know which individual the attacker is targeting, and the attacker is unaware of the honesty level of the responses. However, during training, information about the victim’s identity is provided to the beacon agent, and the honesty rate is provided to the attacker agent for the models to converge faster. This information is removed during inference for the system to be realistic. Additionally, the agent’s objective is to maximize a cumulative reward: The sum of all rewards that will be collected after the end of the current episode, discounted by a factor (0<gamma <1) based on the time t: (R = sum nolimits _{t=0}^{infty } gamma ^t r_t). Finally, a final constant reward is given at the episode’s end based on the success of the agent: Beacon receives it if the victim is not reidentified, or the attacker earns it for reidentifying the victim.
Policies
The outputs of our policies are designed as computable functions that depend on a set of trainable parameters (varvec{theta }). These parameters determine the behavior of the policy by mapping the current state of the environment to optimal actions. The beacon and the attacker are trained using different methods. The beacon uses the Twin Delayed Deep Deterministic Policy Gradient (TD3) [23] algorithm which is suitable for continuous action spaces like the beacon’s. TD3 consists of two components: A policy network (actor) (mu _{theta }(varvec{s}_b)) which selects actions (y_t in {A_b}) and two networks (critics): (Q_{phi 1}^{mu }(varvec{s}_b, h_t)) and (Q_{phi 2}^{mu }(varvec{s}_b, h_t)), which estimate the expected cumulative reward for taking action (h_t). The two critics, (phi _1) and (phi _2), are used to mitigate overestimation bias in Q-value estimates by taking the minimum of their outputs during updates. The critic evaluates the Q-value ((Q^{mu }(varvec{s}_b, h_t))) based on the Bellman equation:
$$begin{aligned} Q^{mu }(varvec{s}_b, h_t) = R_b(varvec{s}_b, h_t) + gamma mathbb {E}_{varvec{s}^{prime }_b sim P(varvec{s}^{prime }_b|varvec{s}_b, h_t)} left[ Q^{mu }(varvec{s}^{prime }_b, mu _{varvec{theta }}(varvec{s}^{prime }_b)) right] end{aligned}$$
(5)
where (varvec{s}_{varvec{b}}^{prime }) is the next state sampled from the environment’s transition model (P(varvec{s}_{varvec{b}}^{prime }|varvec{s}_{varvec{b}}, h_t)). The actor is optimized to deterministically select actions that maximize the value predicted by the critic, following the objective function J: (max J(varvec{theta }_{mu }) = mathbb {E}_{varvec{s}_b} left[ V_{phi 1}(varvec{s}_b, mu _{varvec{theta }}(varvec{s}_b)) right]). The policy (mu _{theta }) is then updated to maximize the expected return as estimated by the critics. This update is performed by adjusting the policy parameters (varvec{theta }_mu) using gradient ascent, (varvec{theta }_{mu } leftarrow varvec{theta }_{mu } + alpha _mu nabla _{varvec{theta }_{mu }} J(varvec{theta }_{mu })), for the policy learning rate (alpha _mu).
The attacker operates in a stochastic and discrete action space which requires a different approach for policy optimization: Proximal Policy Optimization (PPO) [24]. PPO also uses actor and critic networks but in contrast to TD3, (i) it uses a single critic to estimate the value function and (ii) the actor chooses actions probabilistically. We define the attacker’s policy (pi _{theta }) given parameters (theta) and the objective function of PPO to be maximized as follows:
$$begin{aligned} max L(varvec{theta }_{pi }) = mathbb {E}_t left[ min left( frac{pi _{varvec{theta }}(a_t|varvec{s}_{a_{t}})}{pi _{varvec{theta }_{text {old}}}(a_t|varvec{s}_{a_{t}})} hat{A}_t, text {clip} left( frac{pi _{varvec{theta }}(a_t|varvec{s}_{a_{t}})}{pi _{varvec{theta }_{text {old}}}(a_t|varvec{s}_{a_{t}})}, 1 – epsilon , 1 + epsilon right) hat{A}_t right) right] end{aligned}$$
(6)
where (varvec{theta }_{old}) is the vector of policy parameters before the policy update, (epsilon) is the clipping term to control the learning rate, and (hat{A}_t) is an estimator of the advantage function at timestep t which quantifies the benefit of choosing (a_t) over others in a given state.
We train the agents using two approaches: (1) training against predefined static strategies and (2) training against adaptive agents who can dynamically change strategies. Using approach 1, we train the Optimal Beacon Defender (OBD). This agent was trained against both the optimal attacker and a set of regular users. Thus, it learns to detect the optimal attack. However, an optimal attacker may adapt its strategy by querying SNPs outside the MAF order or targeting SNPs that the victim does not carry. OBD cannot defend against this. To model this attacker, we train the Tactical Beacon Attacker TBA using approach 1, against predefined defense strategies from literature (see Compared methods section). To ensure variability and prevent overfitting, in each episode, and randomly switched the opponent’s strategy during training.
Using approach 2, we train the Generic Beacon Defender (GBD) and the Generic Beacon Attacker (GBA) against each other in a two-player setup. The OBD and TBA are used as the starting point to initialize training. To address inherent challenges in multi-agent reinforcement learning (MARL) within adversarial environments, we implemented a structured training framework with a centralized environment and a shared control group accessible to both agents only during training, e.g., publicly available HapMap samples. Please see Discussion section for a discussion on these design choices.
Datasets
We evaluate of our defense techniques using the 164 individuals in the CEU population of the HapMap dataset [25]. We randomly select (i) 40 individuals as the beacon participants; (ii) 50 individuals for the control group of the beacon; and (iii) 50 individuals for the control group of the attacker. This beacon size is the size considered commonly in the literature [3, 4, 6, 15]. In addition, the beacon size has no effect on the attacker’s behavior as it depends on MAF values extracted from the population. For model building, we assume an attack on 10 randomly selected beacon participants. In each episode, the RL-based defense methods select one individual from this group for training, with control groups shared between the attacker and the beacon only during training. The remaining 30 beacon participants are reserved for system testing.
Experimental setup
We trained OBD and TBA over 100,000 episodes, followed by a 25,000 episode fine-tuning phase for the GBD and GBA. We allowed a maximum of 100 queries per episode and performed training cycles every 10 episodes. For the beacon agent, using the TD3 algorithm, training began after 100 episodes of exploration. The agent was trained with a learning rate of (10^{-4}) for both the actor and critic networks, a discount factor (gamma) of 0.99, and a batch size of 256. The replay buffer size was set to (10^4), with policy noise at 20 percent of the maximum action value and noise clipping set at 50 percent to prevent excessive exploration. The TD3 agent was trained for 50 epochs per update cycle. The attacker agent, on the other hand, was trained for 300 epochs per update cycle using a cyclic learning rate scheduler, with a base learning rate of (10^{-5}) and a maximum learning rate of (10^{-3}). We set the discount factor to 0.99 and applied an epsilon clipping threshold (epsilon) of 0.2 to limit policy updates. We defined the g=6 MAF range groups as follows: [0–0.03.03], (0.03,0.1], (0.1,0.2], (0.2,0.3], (0.3,0.4], and (0.4,0.5]. Training took 29 hours for single-agent sessions. Multi-agent fine-tuning took 34 hours. The only set of hyper-parameters in the Stackelberg game is the weights for the privacy and utility terms in the defender’s reward, which we set to 0.85 and 0.15, respectively.
To assess defenses against biased random queries, we model query behavior that deviates from random. We introduce a tunable risk parameter, (l in [0, 1]), to control the querier’s tendency to select rare variants. The probability of selecting a specific SNP j, denoted P(j), is weighted by its MAF such that (P(j)~=~frac{text {MAF}_j^{(1-l)}}{sum nolimits _{k=1}^{m} text {MAF}_k^{(1-l)}}). In this model, the highest risk level ((l=1)) surpasses the MAF bias, resulting in a uniform query distribution where rare SNPs are just as likely to be selected as common ones. On the other hand, decreasing l models more conservative queriers who are less likely to select rare SNPs. We evaluate our defenses against a spectrum of these query behaviors using l values of 0.2 (low-risk), 0.6 (medium-risk), and 1 (high-risk).
We evaluated all reinforcement learning models on a SuperMicro SuperServer 4029GP-TRT with 2 Intel Xeon Gold 6140 Processors (2.3GHz, 24.75M cache) and 256GB RAM. The RL agents were trained using a single NVIDIA GeForce RTX 2080 Ti GPU. The game theory approach was simulated on a SuperMicro SuperServer with 40 cores in parallel (Intel Xeon CPU E5-2650 v3 2.30 GHz).
Compared methods
We compare our methods with the following baselines and state-of-the-art methods the literature. Honest Beacon: The defender responds truthfully to all queries, setting the lower bound for privacy and the upper bound for utility. Baseline Method: The defender flips (k_b) percent of SNVs with the lowest MAF, establishing a lower bound for effectiveness. Random Flips: Proposed by [4], this method randomly flips (epsilon) percent of unique SNVs, enhancing privacy by adding randomness to responses. Query Budget: Also from [4], this method assigns a privacy budget to each individual, limiting their exposure by reducing their contribution to responses after multiple queries. This budget decreases with each query involving the individual, especially for rare alleles, which pose a higher re-identification risk. Once the budget is exhausted, the individual is removed from future queries to preserve their privacy. Strategic Flipping: The Strategic Flipping [7] approach flips (k_s) percent of SNVs in decreasing order of their differential discriminative power, targeting the most informative variants first. Online Greedy (OG) Adaptive: The OG adaptive method, introduced by [10], is an adaptive thresholding based defense method. Here, the beacon has access to a control group. Based on K lowest LRTs on the control group, the beacon calculates a threshold LRT for every new query, and flips the response whenever any individual’s LRT in the beacon falls below this threshold. Simple Recurrent Neural Network (RNN): As a baseline neural network-based solution, we employ a simple RNN to capture the sequential nature of the attacker’s queries. The model uses a 3-layer GRU with an input dimension of 18 and a hidden dimension of 64. It receives the same input as the state of the corresponding RL attacker agent and predicts the degree of honesty through a sigmoid-activated linear classifier. This RNN-based defense model trains against both Optimal and Random attackers for 200 epochs, with a maximum of 300 queries per individual. At the end of each epoch, we switch the victim to ensure generalization across different users.
The parameters for these approaches were selected to balance privacy and utility effectively. Based on the sensitivity analysis conducted by [7], the following parameter values were identified as optimal for achieving this balance: (k_s) = 5, (k_b) = 10, (epsilon) = 0.25, and (beta) = 0.9. The game-theoretic approach of [12] is not directly comparable to our work as it is using a non-LRT-based formulation of risk and it aims at modifying the summary statistics within the system (e.g., allele frequencies) instead of directly altering the beacon responses like we do. The code and the model were also not available.