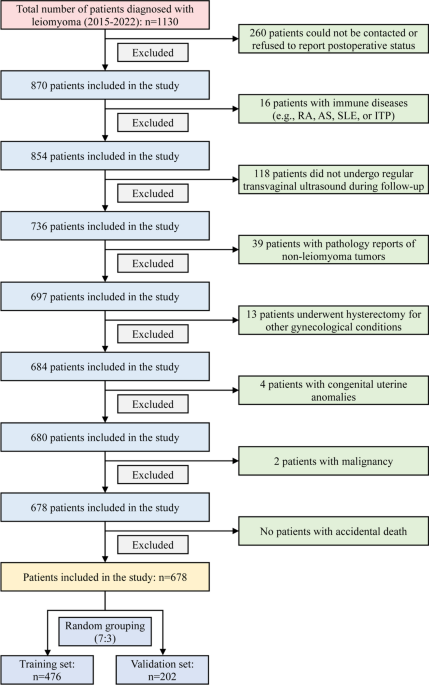
Baseline characteristics
The clinical cases included were randomly divided into a training cohort and a validation cohort at a 7:3 ratio, with a total of 476 cases in the training cohort and 202 cases in the validation cohort. Chi-square tests were used to assess differences in various indicators between the two groups. The results are shown in Table 1, and there were no statistically significant differences between the training and validation cohorts across all indicators (p > 0.05).
Model development
In the training cohort, LASSO regression was applied to identify predictors associated with uterine fibroid recurrence based on clinical variables. The coefficient path plot (Fig. 2A) illustrates how each variable’s regression coefficient changes with the regularization parameter λ. As λ increases, coefficients for less important variables shrink toward zero, leaving only the most relevant predictors. The optimal λ was determined using tenfold cross-validation (Fig. 2B), with the λ corresponding to the minimum mean squared error (left vertical dashed line) selected to reduce overfitting and enhance model robustness. LASSO regression identified six key variables: fibroid subtype (non-submucosal types), MDF, Residue, POP or POC, FH and TVS.
LASSO Regression for Variable Selection. (A) Coefficient path plot; (B) cross-validation curve. The vertical dashed line on the left represents the λ value associated with the minimum mean squared error.
These six variables were subsequently entered into a multivariate binary logistic regression model. As shown in Table 2, submucosal leiomyoma was identified as an independent protective factor (OR = 0.381, P = 0.015). In contrast, postoperative residue (OR = 10.746, P < 0.001), POP or POC (OR = 4.121, P < 0.001), and FH (OR = 2.045, P = 0.003) were significant independent risk factors for recurrence. While a fibroid diameter ≤ 4 cm appeared to confer a protective effect (OR = 0.817), this did not reach statistical significance (P = 0.571). Similarly, the number of fibroids on TVS was not statistically significant (P = 0.129), although a trend toward increased risk with higher counts was observed.
Nomogram for predicting uterine fibroid recurrence after surgery
Based on the multivariate logistic regression results, a nomogram was constructed to predict the risk of fibroid recurrence following myomectomy (Fig. 3). Each of the six predictors included in the model is assigned a point value using a corresponding scale. The total score, obtained by summing the individual scores, yields an estimated probability of recurrence. To demonstrate the application of the nomogram, we selected a representative patient from the study cohort. This patient had a maximum fibroid diameter > 4 cm, a non-submucosal fibroid subtype, postoperative residual fibroids, and four fibroids identified on transvaginal ultrasound (TVS score = 2). The total score calculated was 280, corresponding to an estimated recurrence probability of 87.8%.
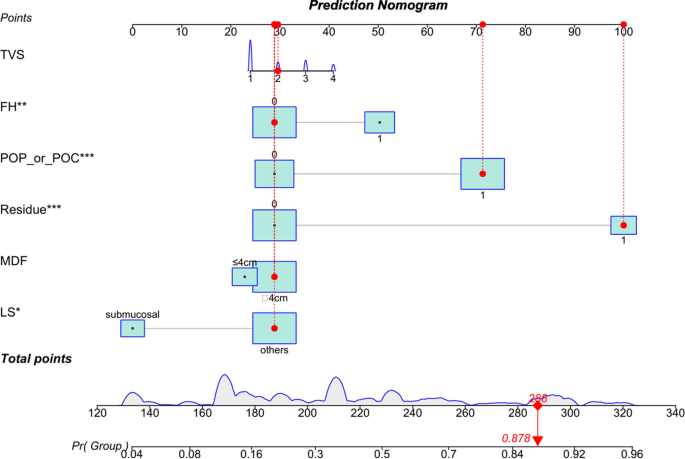
Nomogram for predicting postoperative uterine fibroid recurrence. The model includes six predictors: MDF, LS, POP or POC, Residue, FH, and TVS. Each predictor is assigned a point score, and the total score corresponds to an estimated recurrence probability. Red dashed lines illustrate an example patient. Higher total points indicate a higher probability of fibroid recurrence.
Model evaluation based on validation cohort
To comprehensively evaluate the model’s performance, ROC curves were generated for both the training and validation cohorts based on predicted probabilities and actual outcomes. In addition to the AUC, key classification metrics—including sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and accuracy—were calculated to provide a more complete assessment of predictive performance (Table 3).
In the training cohort, the model yielded an AUC of 0.834 (95% CI: 0.796–0.873) (Fig. 4A), indicating excellent discriminatory ability. In the validation cohort, the AUC was 0.799 (95% CI: 0.737–0.861) (Fig. 4B), demonstrating good generalizability. The C-index derived from ten-fold cross-validation in the training cohort was 0.795 (95% CI: 0.673–0.918), further supporting the model’s robustness and discriminative capability.
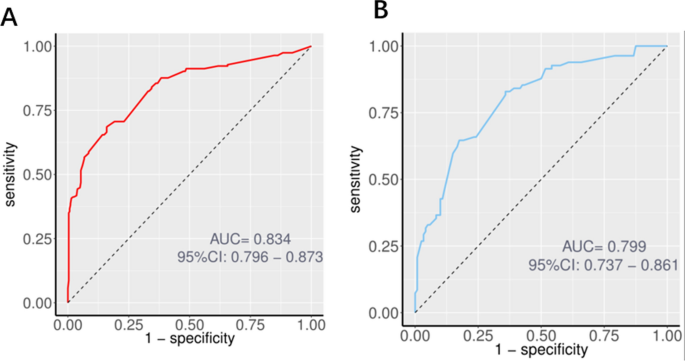
ROC curves for the logistic prediction model. (A) Training cohort (n = 476, AUC = 0.834); (B) Validation cohort (n = 202, AUC = 0.799).
Calibration analysis further demonstrated strong consistency between predicted and observed recurrence probabilities. In the training cohort, the calibration curve (Fig. 5A) closely aligned with the ideal reference line, with a mean absolute error of 0.019. In the validation cohort (Fig. 5B), the calibration curve also showed good agreement, with a mean absolute error of 0.035. These findings suggest that the model exhibits high calibration quality and reliable performance across different datasets.
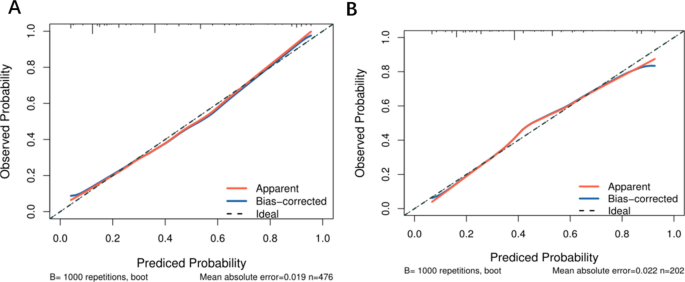
Calibration curves for the logistic prediction model. The red curve indicates the apparent predicted probabilities, the blue curve shows the bootstrap-corrected estimates, and the dashed line represents perfect calibration. (A) Training cohort; (B) Validation cohort.
The Hosmer–Lemeshow goodness-of-fit test (χ2 = 5.362, P = 0.616) indicated no significant deviation between the model’s predicted probabilities and observed outcomes (P > 0.05), supporting its good calibration and overall fit. To further assess clinical applicability, DCA was performed for both the training and validation cohorts (Fig. 6). The DCA curves demonstrated that the prediction model yielded a consistently greater net benefit than the “treat all” or “treat none” strategies across a broad spectrum of threshold probabilities, particularly between 0.1 and 0.5. This threshold range reflects clinically relevant scenarios in which decisions about postoperative surveillance or preventive treatment may be considered. The red curve (training cohort) and blue curve (validation cohort) both lie above the gray line (“All”) and black line (“None”) across this range, suggesting that the model can effectively stratify patients according to their recurrence risk. This enables clinicians to prioritize intervention for high-risk individuals while avoiding unnecessary treatment in low-risk cases. Therefore, the model not only exhibits strong predictive performance but also has the potential to optimise, improving patient outcomes, and enhancing healthcare resource allocation.
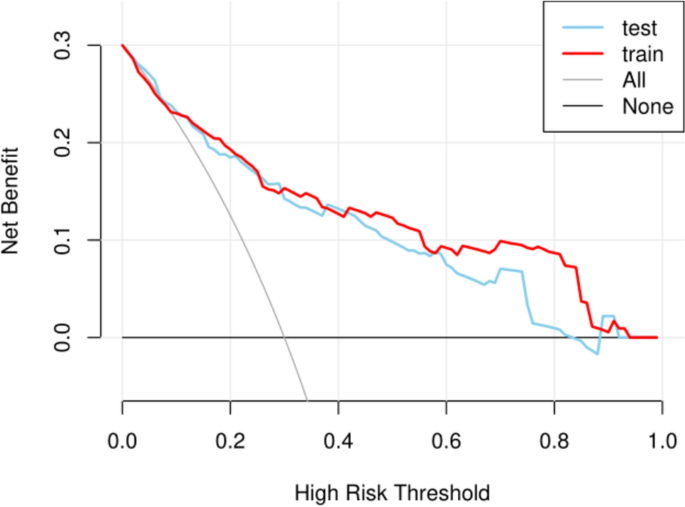
Decision curve analysis for the logistic prediction model. The red line represents the training cohort, and the blue line represents the validation cohort. The gray line (All) assumes all patients receive treatment, while the black line (None) assumes no patient receives treatment.