In this section, we first present the experimental settings of our study. Next, we evaluate our method by comparing it with state-of-the-art methods and report both quantitative and qualitative results. Finally, we explore the impact of basic blocks and various modes on SR performance. Additionally, we assess the effectiveness of our method on edge devices.
Experimental setup
Datasets and Metrics: The dataset contains 25,892 valid infrared image samples, all acquired using five self-developed infrared imaging systems equipped with a 640(times)512 uncooled IRFPA. These 640(times)512 images serves as Ground Truth HR references during the training phase. The corresponding LR images are generated using non-overlapping average pooling operations (e.g., a 2(times)2 kernel for (times)2 downsampling) instead of bicubic interpolation, motivated by our proposed readout circuit structure prior that models the physical infrared imaging process characterized by row-wise scanning and column-wise readout. Average pooling is more consistent with this mechanism and better preserves the spatio-temporal correlations in infrared images, effectively avoiding the artifacts and distortions commonly introduced by interpolation-based downsampling. Furthermore, due to the high cost and limited availability of megapixel-level infrared imaging systems, it is not feasible to obtain real infrared images at a resolution of 1280(times)1024 that are perfectly aligned with the corresponding low-resolution counterparts. To evaluate SR performance at this scale, we generate pseudo HR references using the Upscayl, an image upscaling tool based on an open-source large-scale AI model. Although originally designed for natural image enhancement, Upscayl can reconstruct plausible high-frequency textures that serve as reasonable references for evaluating the quality of our reconstructions images. This approach facilitates the assessment of the performance of our method in the absence of true HR infrared image. The core infrared detectors of all imaging devices have the following key performance parameters: a pixel size of 17 µm, a 640(times)512 focal plane array, a noise equivalent temperature difference (NETD) of 25 mK, a time constant of 8 ms, a frame rate of 50 Hz, and a response wavelength range of 8-14 µm. We utilize 2,500 images to evaluate the performance of different approaches. The supplementary file presents the infrared image datasets utilized in this work, including images acquired from a commercial cooled infrared imaging system, synthetically generated high-resolution infrared images, and validation data obtained from a self-developed uncooled infrared detector. Average peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) are employed as evaluation metrics.
Implementation Details: Different configurations of our proposed EIRSR are presented in Table 1. Data augmentation includes horizontal/vertical flips and random rotations of 90(^circ), 180(^circ), and 270(^circ). The kernel sizes of all convolutions are limited to 3 and 1. The batch size is set to 32, and the size of each ({{I}_{LR}}) is set to (text {48}times text {48}) during the training phase. We employ Adam38 optimizer to train the model with ({{beta }_{text {1}}}=text {0}text {.9}), ({{beta }_{text {2}}}=text {0}text {.999}). The initial learning rate is set to (text {5}times text {1}{{text {0}}^{text {-4}}}) and decays following a cosine learning rate. ({{{L}}_{SR}}) is used to optimize the model over (text {5}times text {1}{{text {0}}^{text {5}}}) iterations, with the initial relaxation factor (alpha) set to 0.2 and is halved every (text {1}times text {1}{{text {0}}^{text {5}}}) iterations. Our method is implemented in PyTorch, and all experiments are conducted on a single GeForce RTX 4090 GPU.
Visual comparison of EIRSR with state-of-the-art methods for (times text {2/}times text {3/}times text {4}) super-resolution. Based on the quantitative results in Table 2, the top six methods from the evaluation are selected, and their difference maps relative to the ground truth images are provided.
Comparison with state-of-the-art methods
To evaluate the effectiveness of EIRSR, we compare it with several advanced efficient SR methods, including RFDN2, LatticeNet28, SwinIR17, ELAN18, BSRN30, ESRT29, HAT19, LKDN31, RGT20, PLKSR32, and SeemoRe14. Table 2 presents the quantitative comparison results of PSNR and SSIM for (times text {2/}times text {3/}times text {4}) upscale factors, along with the number of parameters and Multi-Adds. At scale (times text {2}), the number of parameters and Multi-Adds for our method are 2.54(%) and 2.9(%) of those for the second-ranked method, and 2.77(%) and 2.56(%) of those for the third-ranked method. At scale (times text {3}), the number of parameters and Multi-Adds for our method are 2.74(%) and 3.84(%) of those for the second-ranked method, and 2.51(%) and 3.72(%) of those for the third-ranked method. At scale (times text {4}), the number of parameters and Multi-Adds for our method are 2.54(%) and 3.15(%) of those for the second-ranked method, and 2.77(%) and 2.91(%) of those for the third-ranked method. The results demonstrate that EIRSR, which utilizes a CNN-Transformer structure, surpasses previous leading models in PSNR and SSIM metrics. Comparison results reveal that, for infrared images, Transformer architecture like as HAT19, RGT20, SwinIR17, and ESRT29 outperform the convolutional architecture. This advantage may be attributed to the relationship between the infrared imaging process and the feature split of the Transformer.
In Fig. 5, we present a visual comparison of EIRSR and other efficient methods on (times text {2/}times text {3/}times text {4}). It is evident that the HR images reconstructed by EIRSR exhibit more accurate texture details, particularly along the edges. Compared to Ground Truth (GT) images at scale (times text {2/}times text {3}), our reconstructed images show overall smoothness with no obvious artifacts on the edges, which demonstrates superior visual quality and can be attributed to the incorporation of an image enhancement regularization control term in the loss function. The difference maps at scales (times text {2}) and (times text {3}) show that our method has the smallest discrepancy with the GT images in terms of both overall structure and fine details. The difference map at scale (times text {4}) shows that our method does not generate obvious artifacts. It is worth noting that at a scale of (times text {4}), most methods do not perform well due to the inherent lack of details in infrared images, as the algorithm cannot generate non-existent details. All comparative experiments demonstrate the effectiveness of our method. Furthermore, it is important to emphasize that Transformer-based methods outperform CNNs in infrared image SR, as demonstrated by HAT19 and RGT20. Although the ViT block in both methods employs window-based MHSA, it is essential to recognize that ViT is fundamentally linked to the mechanism of infrared imaging.

Qualitative and quantitative comparison of typical infrared image SR methods. The following sections present localized comparison views of the super-resolution results and their corresponding difference maps with ground truth images.
We present a comparison of the typical SR methods IRSRMamba12 and PSRGAN4 on infrared images, as illustrated in Fig. 6. Our method demonstrates superior performance compared to the current SR methods for infrared images, particularly in terms of image details and visual perception. Furthermore, the differential analysis through error mapping demonstrates that our reconstructed images maintain the closest structural fidelity to the ground truth references in terms of global feature consistency.
Ablation study
In this section, we perform ablation studies on important design elements in the proposed EIRSR to explore the impact of different blocks on infrared image reconstruction performance. Table 3 shows the results.
Effectiveness of CCB and its internal component USCAB. We conduct an ablation study to evaluate the effectiveness of CCB and its internal component USCAB, as shown in Table 3. By masking the CCB, EIRSR reduces to using only the RCTB component. In parallel model, PSNR decreases by 1.42(%) and SSIM decreases by 1.44(%) (see (#)1 and (#)5), while in serial mode, PSNR decreases by 1.65(%) and SSIM decreases by 1.09(%) (see (#)7 and (#)11). This finding confirms that, in the hybrid architecture, the local features extracted by CCB are crucial for establishing effective long-range dependencies between pixels using the RCTB, ultimately improving the network’s performance. Furthermore, we mask USCAB to assess its impact on performance. In parallel model, PSNR degrades by 0.73(%) and SSIM degrades by 1.06% (see (#)1 and (#)2), whereas in the serial mode, PSNR degrades by 0.89(%) and SSIM degrades by 0.25(%) (see (#)7 and (#)8). The USCAB module operates interactively in both channel and spatial dimensions, facilitating the extraction of potential correlations between pixel locality and feature channels. This dual interaction significantly contributes to the improvement of performance in the SR task, especially when integrated with RCTB for global context modeling. These results validate that the CCB, especially when integrated with the USCAB, substantially improves the model’s capacity to extract local features and reinforce local contextual representations. Such localized enhancements are essential for facilitating the global dependency modeling in RCTB, thereby improving both reconstruction quality and overall SR performance in infrared imaging.
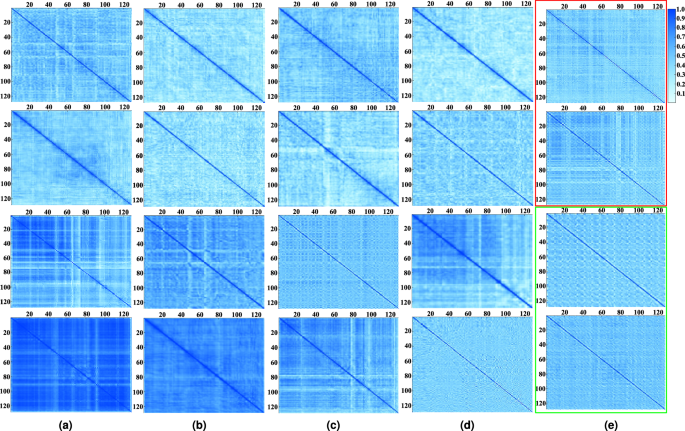
Based on the EIRSR-parallel in Table 3, visualize the cosine correlation between the rows and columns of the 128(times)128 feature maps. (a) Corresponding to # 1 in Table 3, from top to bottom are row correlation in CCB, column correlation in CCB, row correlation in RCTB, and column correlation in RCTB. (b) Corresponding to # 2 in Table 3, from top to bottom are row correlation in CCB, column correlation in CCB, row correlation in RCTB, and column correlation in RCTB. (c) Corresponding to # 3 in Table 3, from top to bottom are row correlation in CCB, column correlation in CCB, row correlation in RCTB, and column correlation in RCTB. (d) Corresponding to # 4 in Table 3, from top to bottom are row correlation in CCB, column correlation in CCB, row correlation in RCTB, and column correlation in RCTB. (e) The red box corresponding to # 5 in Table 3, from top to bottom are the row correlations in RCTB and the column correlations in RCTB. The green box corresponding to # 6 in Table 3, from top to bottom are the row correlations in CCB and the column correlations in RCTB.
Effectiveness of RCTB. We compare the impact of RCTB on SR performance in three cases. When RCTB ((times) rows) operates only in columns, in parallel model, the PSNR degrades by 0.78(%) and the SSIM degrades by 1.1(%) (see (#)1 and (#)3). In serial mode, PSNR degrades by 1.08(%) and SSIM degrades by 0.44(%) (see (#)7 and (#)9). Conversely, when RCTB ((times) cols) operates solely in rows, the parallel model shows a PSNR degradation of 1.32(%) and an SSIM degradation of 1.3(%) (see (#)1 and (#)4), while in serial mode, the PSNR degrades by 1.56(%) and the SSIM degrades by 1.09(%) (see (#)7 and (#)10). In the absence of RCTB, the parallel model exhibits a PSNR degradation of 4.7(%) and an SSIM degradation of 4.12(%) (see (#)1 and (#)6), and in serial mode, the PSNR degrades by 5.0(%) and the SSIM degrades by 3.24(%) (see (#)7 and (#)12). These comparative results demonstrate that applying the transformer to either rows or columns alone is less effective than applying it to both.
The effectiveness of the RCTB is crucial for enhancing the performance of infrared image SR. RCTB is specifically designed to capture long-range dependencies by modeling correlations across rows and columns, a feature particularly important for infrared images where spatio-temporal relationships are critical for accurate reconstruction. Ablation experiments demonstrate that applying RCTB to both rows and columns yields superior performance compared to applying it to rows or columns individually. This indicates that fully applying RCTB enables it to capture interdependencies between pixels across both dimensions, thereby providing comprehensive image features and improving SR quality. Notably, masking RCTB results in significant performance degradation. For instance, in the parallel mode, the PSNR degrades by 4.7(%) and SSIM by 4.12(%), and in the serial mode, PSNR degrades by 5.0(%) and SSIM by 3.24(%). This sharp performance drop underscores the importance of RCTB in capturing global context, solidifying its role as an essential component of our framework. Furthermore, the combination of RCTB and CCB enables a comprehensive feature extraction approach. CCB is responsible for efficiently extracting high-frequency local details, while RCTB handles the long-range global dependencies. By integrating these two modules, our model harnesses their complementary strengths: the CCB enhances local feature representation, whereas the RCTB captures global spatio-temporal correlations grounded in the infrared imaging process. These results underscore the critical role of the RCTB design, which is inspired by the readout characteristics of IRFPA detectors, as essential for performance improvement and not substitutable by conventional designs relying solely on image content or network architecture. The synergy between CCB and RCTB allows the model to capture both fine textures and global coherence, which is critical for infrared image reconstruction. Another critical aspect of RCTB’s design is that it is based on the IRFPA readout circuit. The IRFPA circuit operates by scanning infrared images row-by-row and column-by-column, and RCTB is designed based on this prior knowledge. By incorporating this prior, RCTB effectively models spatio-temporal correlations between pixels across rows and columns, aligning with the structure of the IRFPA readout circuit. This design allows the network to capture semantically richer features from infrared images, significantly improving performance in infrared SR tasks.
In summary, the integration of RCTB with CCB significantly enhances the model’s ability to capture both local and global features. By leveraging the IRFPA readout circuit’s characteristics, RCTB further improves the model’s ability to handle complex dependencies in infrared images, establishing it as a crucial component for high-performance infrared super-resolution.
As illustrated in Fig. 7, we analyze the cosine correlation between rows and columns in features based on the EIRSR-parallel model in Table 3, revealing several noteworthy findings. First, a comparison between Fig. 7a and Fig. 7b demonstrates that integrating CCB enhances RCTB’s ability to capture high-level semantic information by preserving both row and column correlations. This enhancement is attributed to CCB’s efficient extraction of local features, which supports the long-range dependencies modeled by RCTB across rows and columns. In contrast, when CCB is used without USCAB, as shown in the feature correlation maps of Fig. 7b, the model’s ability to maintain row and column correlations within RCTB is significantly reduced, underscoring the critical role of USCAB in preserving these dependencies. Furthermore, as shown in Fig. 7a and Fig. 7c, the absence of row splitting in RCTB leads to a reduction in both row and column correlations, with row correlations being more significantly weakened. This highlights the importance of the row-splitting mechanism in RCTB, which is essential for preserving strong dependencies between pixels across different rows. Similarly, the comparison between Fig. 7a and Fig. 7d demonstrates that removing column splitting results in a reduction in both row and column correlations, with column correlations experiencing a more pronounced decline. This underscores the importance of column splitting in RCTB for capturing global dependencies between columns, a critical factor for accurately modeling pixel relationships in infrared images. Additionally, the comparison of the red and green boxes in Fig. 7e reveals that RCTB demonstrates a superior ability to model row and column correlations compared to CCB alone. This further emphasizes RCTB’s unique capacity to capture long-range dependencies and spatial-temporal correlations across rows and columns, a key factor in enhancing SR performance. Overall, the results shown in Fig. 7 indicate that column correlations are more prominent than row correlations. This phenomenon can be attributed to the architecture of the IRFPA readout circuit, where each column of pixels shares a single readout channel, resulting in stronger column-wise correlations. By leveraging this inherent structure, RCTB enhances the modeling of interdependencies across rows and columns, leading to significant improvements in infrared image SR performance.

The effect of the control term in the loss function on (times)2 SR. (a) The top represents the local zoom of GT image, and the bottom represents the SR without control term. (b) Top represents GT image with guided filtering, and bottom represents image preprocessing in the control item is guided filtering. (c) The top represents GT image with guided filtering and image enhancement, the bottom represents image preprocessing in the control item are guided filtering and image enhancement.
Loss function. We introduce a regularization control term into the loss function and dynamically adjust this loss function using a relaxation factor (alpha) during training, which yields interesting results, as illustrated in Fig. 8. Sub-image (a) shows that without the introduction of control terms, our method produces more noise than GT images, resulting in unsatisfactory outcomes. In sub-image (b), we observe that with the introduction of the control item, ({{tau }_{prep}}left( I_{HR}^{i} right))represents (I_{HR}^{i}) processed by guided filtering and demonstrates superior performance compared to the GT image processed directly by guided filtering. Furthermore, in sub-image (c), where ({{tau }_{prep}}left( I_{HR}^{i} right)) refers to the application of guided filtering and detail enhancement (Laplacian sharpening) on (I_{HR}^{i}), our method outperforms the direct application of guided filtering and detail enhancement on GT images in the terms of image detail. The computational profiling conduct on the RK3588 Core Board reveals clear temporal characteristics: standalone guided filtering and Laplacian sharpening operations require 18.79 ms and 6.701 ms respectively under single-threaded mode. Our integrated architecture, which combines these preprocessing operators, demonstrated 37.815 ms processing latency. Compared to the conventional sequential approach (18.79 ms + 6.701 ms + 37.815 ms), the proposed end-to-end implementation achieves a 40.27(%) reduction in total execution time. The experimental analysis of the loss function encourages us to investigate the integration of the infrared image preprocessing algorithm into the network in future research by incorporating the control term into the loss function, with the aim of reducing the computational cost associated with infrared imaging system preprocessing and minimizing overall processing latency.
SR comparison under different readout modes
To validate the effectiveness of the proposed spatio-temporal readout prior, we conduct a comparative experiment using infrared images acquired by a self-developed infrared imaging system and a commercial infrared imaging system, operating in rolling shutter and global shutter readout modes, respectively. The IRFPA in the self-developed system operates in a rolling shutter readout mode, which performs row-wise scanning and column-wise readout, in contrast to the commercial system that adopts a global shutter readout mode. The commercial system features a pixel size of 15 µm, a 640(times)512 focal plane array, and a noise equivalent temperature difference (NETD) (le) 17 mK. A total of 2,500 images are used for validation in both the rolling shutter and global shutter imaging systems. The average results of the quantitative comparison are summarized in Table 4. As shown in Table 4, the spatio-temporal readout prior-based method achieves PSNR improvements of 6.94(%) and 9.65(%), and SSIM improvements of 2.65(%) and 6.68(%) on the rolling shutter imaging system, compared to its performance on the global shutter system, under (times)2 and (times)4 upscaling factors, respectively.

Qualitative and Quantitative Comparison of Super-Resolution Performance in Infrared Imaging Systems with Different Readout Modes. (a) Self-developed imaging system (Rolling Shutter Readout Mode). (b) Commercial imaging system (Global Shutter Readout Mode).
Representative comparison images are selected from different imaging systems under (times)2 and (times)4 upscaling factors, and their corresponding PSNR, SSIM, and difference maps are computed, as illustrated in Fig. 9. As shown in Fig. 9, the proposed method achieves better performance on the self-developed imaging system that incorporates spatio-temporal readout priors, whereas its effectiveness is less pronounced on the global shutter imaging system, which lacks such priors. Specifically, under the (times)4 SR scenario, it fails to reconstruct the vertical structural components of the glass curtain wall on the global shutter imaging system, leading to a reconstruction that retains only the horizontal stripe patterns, with the vertical features entirely absent. The comparative results across different imaging modes support the effectiveness of the proposed method that incorporates spatio-temporal readout priors. Moreover, these findings imply that accounting for hardware-level imaging characteristics can be beneficial to the performance of SR tasks. This further underscores the design specificity of our network design for row-wise scanning and column-wise readout IRFPAs, in which spatio-temporal readout priors play a crucial role in guiding the reconstruction process. While this specificity contributes to significant performance improvements on row-column scanned systems, it also underscores the need to adapt our framework for other imaging sensor architectures–such as global shutter or event-based imaging systems–where differing physical imaging process and spatio-temporal dynamics may necessitate alternative modeling approaches.
Edge device deployment
To validate the effectiveness of our model on edge devices, we optimized EIRSR-T as EIRSR-T-opt and evaluated it on an edge inference device: RK3588 Core Board, an embedded system-on-module (SoM) from Rockchip, which features three integrated NPU cores. We assessed the performance of models at a scale of (times text {2}) in single-process mode, utilizing 16-bit floating point precision during inference. For each input image size, we executed the models for two hours to avoid the warm-up effect, the results are presented in Table 5. As the size of the input image increases, there is a corresponding rise in power consumption, memory usage, memory read/write operations, and runtime for the model. In single-threaded mode, models with low power consumption can be deployed to edge devices. However, our optimized model cannot achieve real-time processing speeds in the single-threaded mode with an input size of 1280(times)1024. In this case, real-time SR for large images can be achieved through multi-core and multi-threaded processing, but this approach significantly increases the resources consumption of edge devices. Table 5 illustrates that memory usage and memory read/write operations are significant bottlenecks that limit the model’s performance. To facilitate deployment on edge devices, we have summarized several guidelines for model optimization. Specifically, the following strategies are recommended: consider operator fusion whenever possible, implement weight sharing during model quantization, ensure that the number of feature channels is a multiple of four, adopt a general 3(times)3 convolution kernel, reduce the number of heads in MHSA, maximize the split of row and column features, and utilize operators that are optimized for the specific hardware platform.
Motivation and applicability of the hardware prior
Our method is inspired by the row-wise scanning and column-wise readout mechanism of our self-developed uncooled IRFPA detectors. This readout mechanism introduces inherent temporal correlations among row pixels and spatial correlations among column pixels during the image formation process, both of which are explicitly exploited in our model design. To capture these correlations, we propose the RCTB, which applies self-attention separately along the row and column dimensions. This design aligns closely with the physical imaging mechanism and enables the network to effectively capture pixel-level dependencies introduced by the readout circuitry, thereby yielding improvements in SR performance, as demonstrated in our ablation studies. While our method is tailored to IRFPAs exhibiting such readout characteristics, this class of imaging sensors is widely deployed in low-power, cost-sensitive, and edge-oriented infrared imaging systems. Therefore, the proposed method has considerable potential for practical deployment.
We also acknowledge that the method is not directly applicable to global shutter mode imaging sensors, which lack the row-column spatio-temporal dependencies leveraged in our design. As demonstrated in the “SR Comparison under Different Readout Modes,” the method exhibits reduced effectiveness. Nonetheless, the principle of incorporating hardware-level priors into network design can be extended to other imaging architectures through appropriate modifications, which we aim to explore in future work. Compared with previous infrared SR methods that focus solely on images or networks, our approach is the first to integrate the imaging circuitry structure priors into the network architecture. This allows for more efficient modeling of spatio-temporal correlations that are consistent with the hardware, leading to enhanced reconstruction fidelity and robustness in the infrared SR task.