Chirality is traditionally viewed as a structural property of matter. The spatial arrangement of atoms in molecules and materials indeed defines their handedness. In a simplified view, structural chirality is often used to explain chiral recognition. However, recent research indicates that structural chirality is insufficient to fully understand chiral phenomena. In particular, growing evidence points to a functional role of chiral electron dynamics in enabling and mediating chiral interactions at the electronic level5. Such dynamics are also thought to play a role in advanced applications, including spintronics6, unidirectional molecular machines7 and chiral-sensitive biosensing8. Furthermore, a wide range of chiroptical techniques, such as electronic circular dichroism9 (CD), PECD10,11 and chiral high-harmonic generation12,13, are now understood to examine the underlying chiral dynamics of electrons rather than merely structural asymmetries. These developments motivate a broader perspective on chirality that encompasses not only static structure but also the dynamic behaviour of electrons in chiral systems.
In spite of the fundamental importance of chiral electron dynamics, spectroscopy based on attosecond pulses has so far been lacking the crucial capability of chiral discrimination. The key obstacle for expanding attosecond science into the realms of chiral molecules and materials has been the lack of circularly polarized attosecond light pulses. As a consequence, all pioneering experiments in this field have relied on femtosecond pulses, for example, refs. 12,13,14,15,16,17,18,19,20,21. Notably, strong-field ionization with intense two-colour femtosecond laser pulses has been used to measure phase shifts17 and control the asymmetry of photoelectron angular distributions (PADs) in the strong-field ionization of chiral molecules20,22. Recently, some of the present authors have developed attosecond metrology in circular polarization by introducing a plug-in apparatus for the generation and demonstration of a general methodology for the complete characterization of circularly polarized attosecond pulses1. This new capability has recently been applied to study the photoionization dynamics of atoms2,23.
Here we introduce attosecond chiroptical spectroscopy by reporting the first application of circularly polarized attosecond pulses to chiral molecules. This development, combined with momentum-vector-resolved electron-ion-coincidence spectroscopy, allows us to measure and control chiral electron dynamics on their natural attosecond timescale. Specifically, our study demonstrates attosecond coherent control over PECD based on the constructive or destructive interference between pairs of well-defined photoionization pathways. It also reveals the characteristic dependence of chiral photoionization delays on both the polar and the azimuthal angles of photoemission in the light-propagation frame.
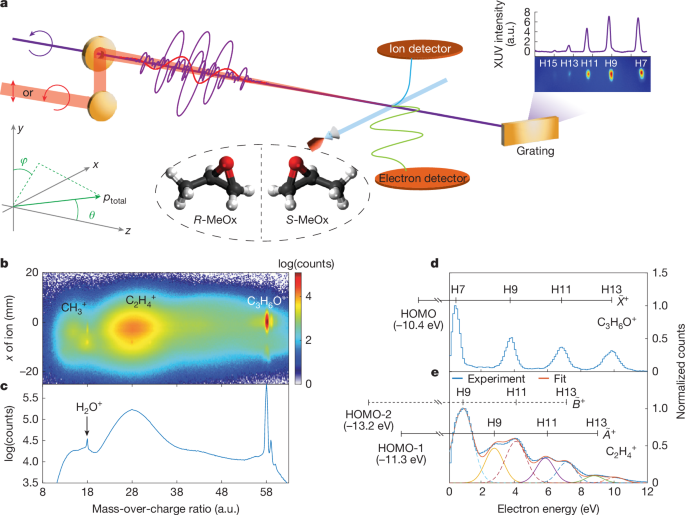
The experimental set-up is illustrated in Fig. 1a, with details given in Methods. The circularly polarized extreme-ultraviolet (XUV) attosecond pulse train (APT) of a single, common helicity was produced by the non-collinear HHG scheme using a compact plug-in apparatus1. A weak linearly or circularly polarized (co-rotating) near-IR (800 nm) laser pulse was spatio-temporally overlapped with the XUV APT with attosecond temporal stability to induce XUV-IR two-photon transitions using the reconstruction of attosecond beating by interference of two-photon transitions (RABBIT) approach. In this study, we define the light-propagation direction to be the z axis and the light polarization to be in the x–y plane, so that the CD manifests itself in the angular distribution with respect to the angle θ = arccos(pz/ptotal), in which ptotal and pz are the total momentum of the electron and its z component, respectively. The azimuthal angle in the polarization plane ϕ = atan(px/py) was integrated over from −15° to +15°. Enantiomerically pure samples of methyloxirane (MeOx, also known as propylene oxide, C3H6O, ≥99.5% ee) were delivered into a cold-target recoil-ion-momentum spectroscopy (COLTRIMS) set-up24,25 by supersonic expansion through the nozzle with an aperture of 30 µm. The 3D momenta of photoelectrons and ionic fragments were measured in coincidence in the ultrahigh-vacuum chamber (about 10−10 mbar).
a, Experimental set-up. The ionic fragments and emitted photoelectrons are measured in coincidence using COLTRIMS. b, Measured 2D ionic spectrum as a function of the mass-over-charge ratio and the position on the ion detector along the molecular-beam direction in the presence of the XUV field only. c, The projection of the distribution in b on the mass-over-charge axis. Note that the counts are shown on a logarithmic scale. The two small peaks above m/q = 58 correspond to 13C isotopomers of the parent ion. d,e, Measured photoelectron spectra in coincidence with the intact parent ion (d) and the C2H4+ fragment ion (e). In d, the observation of a series of discrete equidistant peaks confirms that photoionization to the ({mathop{X}limits^{ sim }}^{+}) ground state of the cation leaves the molecule intact. In e, the experimental data are fitted by two sets of Gaussian peaks corresponding to the ({widetilde{A}}^{+}) and ({widetilde{B}}^{+}) ionic states, respectively. The ionization energies of the relevant states are taken from the ref. 26. a.u., arbitrary units.
Figure 1b shows the ionic fragment distribution as a function of mass-over-charge ratio (m/q) and detector position and Fig. 1c presents the projection onto the m/q axis, both recorded using attosecond XUV pulses only. After photoionization by the attosecond pulses comprising harmonic 7 (H7) to harmonic 13 (H13), we observe the undissociated parent ion (C3H6O+) and two broader distributions assigned to CH3+ and C2H4+ fragments, in agreement with previous synchrotron studies26. The photoelectron spectrum identifies the electronic state of the ion that was accessed in the ionization step, whereas the ionic species reveal whether and how a given electronic state of the ion dissociates. Figure 1d,e shows the photoelectron spectra measured in coincidence with the parent ion and C2H4+, respectively. The former reflects photoionization from the highest occupied molecular orbital (HOMO) by H7–H13, which leaves the cation intact. The photoelectron spectrum measured in coincidence with C2H4+ shows a more complex distribution, which contains contributions from the ({widetilde{A}}^{+}) and ({widetilde{B}}^{+}) ionic states. In this study, we focus on the parent-ion channel.
Figure 2 shows the measured PECD and its coherent control by changing the XUV-IR delay with attosecond precision for the parent-ion channel. The energy (Ek)-resolved and angle (θ)-resolved PECD distribution is defined by 2(IS(Ek, θ) − IR(Ek, θ))/(IS(Ek, θ) + IR(Ek, θ)), in which IS/R(Ek, θ) is the PAD of the S/R enantiomer. The chiral nature of PECD has also been verified by switching the XUV helicity. Figure 2a,b shows the measured PECD distributions obtained from the XUV field only and the delay-averaged result in the XUV + IR two-colour fields, respectively. For the XUV-only PECD distribution, the four dipole-shaped concentric rings correspond to the four main peaks shown in Fig. 1d. After introducing an IR field (Fig. 2b), sidebands (SBs) appear between the main peaks and inherit the PECD sign of the neighbouring main peaks but with some angular modulations, a consequence of the fact that extra partial waves are involved in the two-photon-ionization process (see the ‘Theoretical methods’ section for the details). The asymmetry parameters are obtained by fitting trigonometric functions to the angle-resolved PECD, with the results shown in Extended Data Fig. 1. Figure 2c compares the extracted PECD values in the XUV-only and XUV + IR cases. In the XUV-only case, the highest PECD amounts to about 10%. In the presence of a linearly polarized IR field, the PECDs at the SB positions are enhanced by up to 5% compared with the average PECD of the neighbouring main bands. In the presence of a circularly polarized IR field, the SB PECDs are increased much more, which is in line with predictions from ref. 4 and simulations performed for MeOx. Typically, the PECD values are doubled compared with the average of their neighbouring main bands, as indicated by the black arrow in Fig. 2c. In the XUV + IR field, the PECD can also be actively controlled. Figure 2d shows the delay-resolved PECD in the presence of a linearly polarized IR field. The PECDs at all SB positions are modulated with a period of 1.33 fs, with a maximal modulation depth at SB 14, at which the PECD even changes sign. The phase shifts between the PECD oscillations of different SBs are dominated by the attochirp of the XUV APT. The delay-dependent PECDs in the case of a circularly polarized IR field is shown in Extended Data Fig. 2.
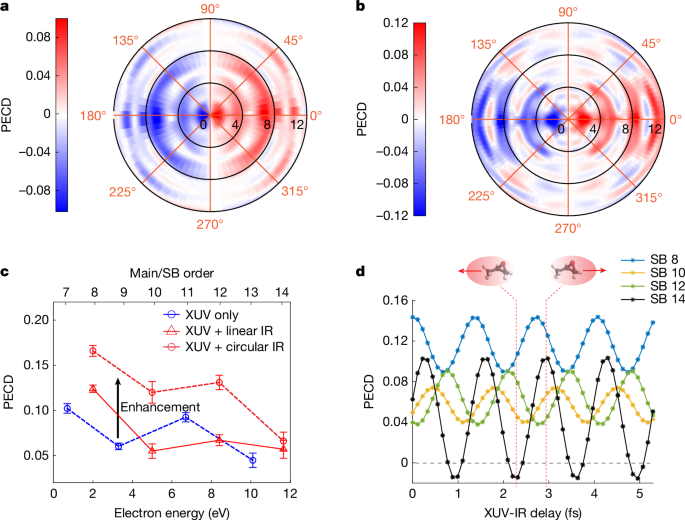
a,b, Measured angle-resolved and energy-resolved PECD distributions in the XUV-only case and the XUV + IR case with linearly polarized IR field, respectively. c, Comparison of PECD values between XUV-only photoionization and the (delay-averaged) XUV + IR two-colour photoionization, including both linear and co-rotating circular polarizations of the IR field. d, Measured PECD values at SBs 8, 10, 12 and 14 as a function of the XUV-IR delay for a linearly polarized IR field. The photoelectron signals have been integrated over a window of width 0.5 eV centred at the peaks of the main bands and SBs. The insets above panel d illustrate the PECD reversal observed in SB 14.
We now discuss the measurement of chiral asymmetries in molecular photoionization delays, starting with the case of a linearly polarized IR field. As in the case of PECD, this approach isolates the chiral signatures of the one-photon XUV transition and eliminates possible chiral contributions from continuum–continuum transitions driven by the IR field4. Figure 3a,c shows the energy-resolved RABBIT traces obtained by integrating over the photoelectron emission angle θ from 0° to 90° (forward-emitted photoelectrons) or from 90° to 180° (backward-emitted photoelectrons). The phases of the photoelectron-yield oscillations at the SB positions have contributions from both the attochirp and the molecular photoionization delays. By evaluating the phase difference between forward-emitted and backward-emitted photoelectrons, the influence of the attochirp is cancelled, isolating the chiral asymmetry of the molecular photoionization delays. Figure 3d compares the yield oscillations of forward and backward photoelectrons for different SBs, after removal of the slowly varying background by Fourier transformation (see Methods for details). The forward photoelectrons are temporally behind the backward photoelectrons in the case of R-MeOx, that is, the SB maxima occur at larger XUV-IR delays, an effect that is most prominent for SB 8.
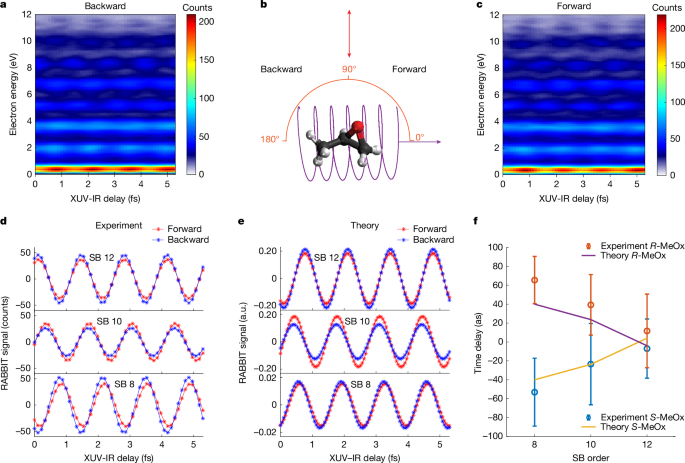
Data were acquired with a linearly polarized IR along the y direction and the photoemission angle ϕ was integrated over from −15° to +15°. a,c, RABBIT traces of backward electrons (θ is integrated over from 90° to 180°) and forward electrons (θ is integrated over from 0 to 90°), respectively, as shown in panel b. d,e, Measured and simulated energy-integrated RABBIT signals for SBs 8, 10 and 12, for which the constant background signals have been removed using Fourier transformation. The electron-energy integration width is 0.5 eV centred at the peak positions. f, Experimental and theoretical forward–backward photoionization time delay as a function of photoelectron energy for both enantiomers of MeOx. Note that the experimental results in panels a, c, d and the theoretical results in panel e correspond to R-MeOx and the data for S-MeOx are shown in Extended Data Fig. 3. a.u., arbitrary units.
The same measurements performed on the other enantiomer (S-MeOx; Extended Data Fig. 3) showed opposite delays, demonstrating their chiral nature. Figure 3f shows the measured photoionization time delays for both enantiomers. We find that the forward–backward time delays, expressing the temporal separation of the forward-emitted and backward-emitted photoelectron wave packets, amounts to about 60 as at SB 8 and decreases with electron kinetic energy, which reflects the decreasing sensitivity of the photoelectron wave packet to the chirality of the molecular potential, as in the case of PECD amplitudes. The calculated time delays are slightly smaller than the measured ones but lie within the error bars of the measurement. The chiral nature of these forward–backward time delays is confirmed by the opposite signs of the time delays obtained for the two enantiomers in both experiment and theory.
The molecular photoionization dynamics are simulated by adapting the theoretical framework of ref. 4, which suggested making use of RABBIT to realize the coherent control of chiral signatures in the PAD. The simulations are performed in the frozen-core static-exchange and electric-dipole approximations, following refs. 3,4,27 with the modifications described in Methods to remedy the effect of artificial resonances caused by the discretization of the photoelectron continuum and to account for the experimental conditions.
The original theory proposal discussed photoelectron interferometry for the model chiral molecule CHBrClF (ref. 4). Compared with CHBrClF, MeOx shows a more isotropic nature, as can be seen from the smaller number of angular basis functions needed to represent the molecular wavefunctions for MeOx compared with CHBrClF (see Methods). This suggests that the photoelectrons of CHBrClF experience higher anisotropy in the molecular potential. To what extent does this influence the robustness of the control scheme? Simulations for CHBrClF in ref. 4 showed that the maximum PECD signal could be enhanced by a factor of five by optimizing the XUV-IR delay, whereas in the simulations for MeOx, optimizing the delay can increase the PECD by about a factor of two, which is a similar enhancement as the delay-averaged experimental results presented in Fig. 2. This may indicate that the presented control scheme could benefit from a less isotropic nature of the molecule. A similar argument can be made when analysing the dependence of the chiral signatures on the photoelectron energy. The PECD as well as the forward–backward time delays decrease with the SB order as shown in Figs. 2c and 3f. Nevertheless, introducing the circularly polarized IR pulse increases the PECD by about 50% for the highest SB (SB 14) compared with the PECD signal of the closest harmonic (H13) in the XUV-only case. The calculation of chiral photoionization delays has been reported in a recent publication28.
In addition to the chiral forward–backward time delays, the 3D momentum resolution of our experiment allows us to obtain the photoionization time delays with angular resolution. Momentum-vector resolution is a prerequisite for a quantitative measurement of chiral photoionization delays because the latter depend on both laboratory-frame angles of photoemission (θ and ϕ) in any chiral-sensitive experiment. Extended Data Fig. 4 illustrates this fact by showing that the phase of the SB oscillation linearly depends on ϕ in the case of co-rotating XUV and IR fields. This is the RABBIT analogue of the angular streaking principle. Taking this property into account allows us to perform a quantitative analysis of angle-resolved chiral photoionization delays. Figure 4a,b shows the measured θ-resolved RABBIT traces of SB 8 for the two enantiomers of MeOx in the case of a co-rotating circularly polarized IR field, the configuration that yields the largest PECD enhancement in line with theoretical calculations. The RABBIT fringes are not vertical but show a tilt as a function of θ, in a direction that inverts when exchanging the enantiomers, again demonstrating the chiral nature of the effect. The time delays extracted at each θ angle (relative to θ = 90°) are shown in Fig. 4c. They vary by about 240 as over the investigated angular range. Figure 4d,e shows the calculated angle-resolved RABBIT traces for the two enantiomers, respectively, closely reproducing the opposite tilts of the RABBIT fringes for the two enantiomers. The angle-resolved photoionization delays shown in Fig. 4f closely reproduce the measured variation of the photoionization delays by about 240 as over the measured angular range. The remaining differences between the theoretical results and the experimental data may originate from non-dipole effects, non-perturbative effects in the light–molecule interaction or electronic correlation effects. The experiment was performed well within the perturbative regime and the results shown in Fig. 2a,b do not provide evidence for strong non-dipole effects. We therefore expect electronic correlations to be the primary cause for deviations between experiment and simulations.
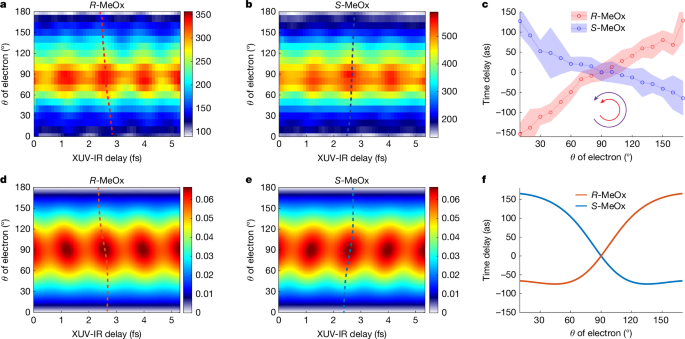
a,b, θ-resolved RABBIT traces of SB 8 for the R and S enantiomers of MeOx. c, The extracted photoionization time delay from a and b, for which the delay values at θ = 90° were chosen as reference. Note that the negative value of the ionization time delay indicates that the photoelectron wave packet is delayed with respect to emission at θ = 90°, chosen as the reference in these measurements. The θ-dependent maxima are highlighted in a and b as dashed lines and the equivalent lines are shown in d and e. The uncertainty of the extracted time delay (error bar) is estimated by the background-over-signal approach34. d–f, The corresponding results from theoretical calculations described in the text and in Methods.
The comparison of angle-resolved time delays obtained with circularly or linearly polarized IR pulses also provides insights into the contribution of the continuum–continuum transitions to the chiral asymmetries of the time delays. Extended Data Fig. 5 shows such a direct comparison, with panels a and b displaying the raw experimental data for the case of a linearly polarized IR field and panels c and d comparing the angle-dependent photoionization time delays for linearly and circularly polarized IR fields, respectively. Whereas the delay variation amounts to approximately 180 as in the case of a linear IR field, it reaches approximately 240 as in the case of a circularly polarized IR field. To quantify the chiral asymmetry contributed by the continuum–continuum transitions, panel e shows the symmetrized time delays for a given polarization configuration (obtained as (τ(θ)S-MeOx + τ(180° − θ)R-MeOx)/2) and panel f shows their difference, which quantifies the chiral contribution of the continuum–continuum transitions to the measured photoionization delays. Although the error ranges overlap with zero, a clear trend can be recognized, corresponding to a variation of roughly 60 as over the whole angular range that we assign to the chirality of the IR-induced continuum–continuum transitions in the chiral potential.
A comparison of the present results, obtained with circularly polarized attosecond pulses in the perturbative regime, with previous results, obtained with femtosecond pulses in the strong-field regime17,20,22, further highlights the achieved advances. The perturbative nature of the present approach results in a transparent control mechanism and good agreement with calculations. In the present work, the naturally occurring PECD effect has been enhanced by a factor of two, reaching up to 16%, and has been coherently controlled on the attosecond timescale in the perturbative regime involving pathways driven by one XUV and one IR photon each. Using femtosecond pulses, Rozen et al. observed asymmetries of up to 0.5% and their coherent control using non-perturbative two-colour strong-field ionization, but a detailed understanding of the mechanism as well as agreement with theory were missing20. In this work, we have measured chirality-sensitive photoionization delays by advancing the established RABBIT technique to circularly polarized attosecond pulses. The photoionization delays have been measured with 3D momentum resolution, in coincidence with specific ionic fragments and resolved in terms of the cationic final states. Good agreement with theory and a transparent explanation of the underlying mechanisms have been provided. By contrast, Beaulieu et al.17 have used strong-field ionization based on non-perturbative two-colour femtosecond pulses. They have measured the projection of the PAD on a 2D detector parallel to the propagation direction of the laser pulses. This geometry does not resolve the emission angle in the polarization plane of the laser pulses on which the photoionization delay depends. Moreover, the photoionization delays determined in two-colour strong-field ionization depend on the intensity of the laser pulses29, such that they do not represent intrinsic molecular properties.
In conclusion, we have introduced attosecond chiroptical spectroscopy and applied it to resolve and control the photoionization dynamics of chiral molecules on their natural, attosecond timescale. Our study demonstrates the powerful capability of the combination of circularly polarized attosecond light pulses with the 3D-momentum-resolved electron-ion coincidence detection, which allows examination of the attosecond electron dynamics induced by photoionization in an electronic-state-resolved, angle-resolved, energy-resolved and enantiomer-resolved manner. Electron scattering in a chiral molecular potential gives rise to the asymmetric scattering amplitudes with respect to the light-propagation direction, underlying the PECD phenomenon, which has high chiral sensitivity and broad applicability. Attosecond chiroptical spectroscopy has now also revealed that one-photon-ionization delays of chiral molecules also show chiral asymmetries, defining a general approach to time resolve the electron-scattering dynamics in chiral molecules. Attosecond chiroptical spectroscopy also has the potential of answering a very important question about the origin of the chirality-induced spin selectivity (CISS) effect30, which still lacks a quantitative explanation. Whereas traditional approaches view CISS as a purely electronic (spin–orbit) effect, such models underestimate the CISS effect by typically two orders of magnitude31. Very recent models suggest that coupled electronic-nuclear dynamics could play a central role32. Attosecond chiroptical spectroscopy may offer a solution to this intriguing puzzle through its ability of temporally separating electronic from structural dynamics33.