Quantum Metrics Analysis Of 20,000 States Reveals Relationships Between Entanglement And Fisher Information

The pursuit of enhanced precision in measurement drives innovation across numerous scientific fields, and quantum mechanics offers the potential to surpass classical limits. Volkan Erol from Marmara University and colleagues investigate the connection between quantum entanglement, a uniquely quantum phenomenon, and the ultimate precision achievable in measurements. Their work demonstrates strong, predictable relationships between different measures of entanglement and a key indicator of measurement sensitivity, known as Maximized Fisher Information. Through extensive analysis of thousands of quantum states, the researchers empirically validate theoretical predictions about how entanglement translates into metrological advantage, establishing fundamental limits for optimising sensing protocols and resource allocation in real-world applications. The team’s findings offer crucial guidance for designing quantum sensors with demonstrably improved performance.

Entanglement, Metrology, and Decoherence Limits

This research provides a comprehensive investigation into the relationship between quantum entanglement, quantum metrology, the science of improving measurement precision, and the practical limitations imposed by decoherence, the loss of quantum coherence. The central aim is to quantitatively understand how entanglement enhances measurement precision and to establish practical guidelines for designing quantum sensors that leverage entanglement while remaining robust to noise. The work blends theoretical analysis with a focus on real-world applicability, moving beyond simply demonstrating entanglement-enhanced metrology to optimizing it. Quantum metrology utilizes quantum phenomena, such as entanglement, to surpass the precision limits of classical physics.

Entanglement links two or more particles, meaning their fates are intertwined even when separated by large distances. Fisher information, a mathematical tool, quantifies how much information a measurement provides about an unknown parameter, with higher values indicating greater precision. The study explores various ways to quantify entanglement, including concurrence, negativity, and entanglement of formation, all applied to two-qubit systems. The authors employ a combination of theoretical analysis, numerical simulations, and robustness analysis to explore how entangled systems behave under various conditions.

They optimize entanglement levels and measurement strategies to maximize precision, and compare the usefulness of different entanglement measures for predicting metrological performance. The research confirms that entanglement improves measurement precision beyond the classical limit, but reveals that there is an optimal level; too little provides insufficient enhancement, while too much can be detrimental due to increased sensitivity to noise. The optimal level is found to be moderate. Simply creating an entangled state is not enough; the measurement strategy, how the entangled state is probed, must be optimized to fully realize the potential for enhanced precision.

The authors emphasize techniques that maximize Fisher information. Surprisingly, entanglement-enhanced metrology can be robust to decoherence, particularly to phase damping, a type of decoherence affecting the relative phase between quantum states. The best metrological performance is achieved with moderate levels of entanglement, and even separable, non-entangled states possess significant metrological utility, highlighting the importance of quantum coherence beyond entanglement. These findings provide crucial insights for designing quantum sensors. This work builds upon and extends previous research in quantum metrology by providing a more comprehensive analysis of the relationship between entanglement and precision, investigating the effects of decoherence in greater detail, and developing practical guidelines for designing quantum sensors.

The research also compares the performance of different entanglement measures and emphasizes the importance of measurement strategy optimization. Future research directions include exploring more complex entangled states, developing more robust methods for protecting entangled states from decoherence, and applying these techniques to real-world sensing applications. Ultimately, this paper provides a rigorous and practical framework for understanding and harnessing the power of entanglement for precision measurement.

Entanglement Measures and Metrological Precision Analysis

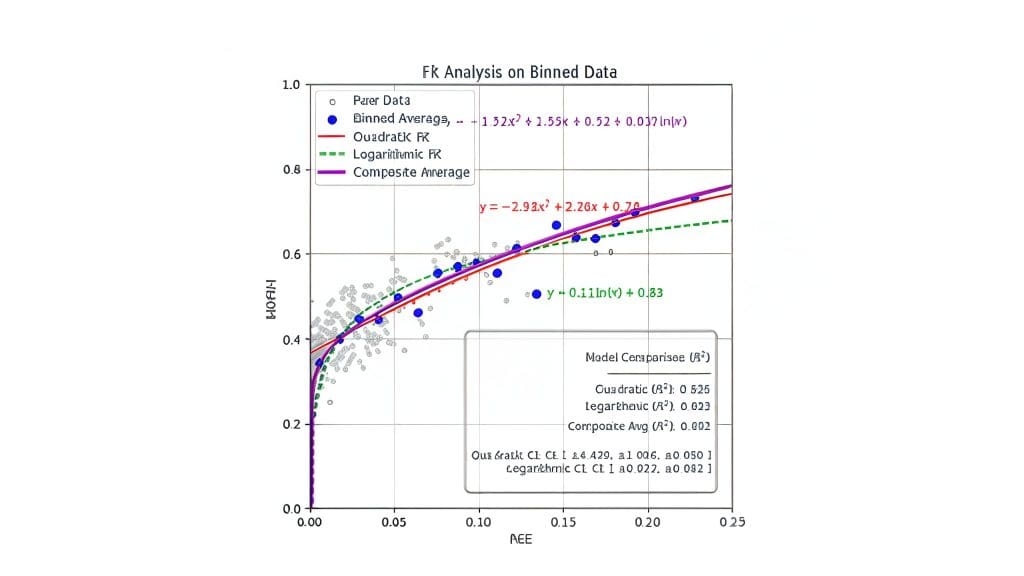
This study pioneers a comprehensive methodology for investigating the relationship between quantum entanglement and metrological precision, beginning with the generation of 20,000 randomly generated two-qubit states. Researchers then calculated three distinct entanglement measures, concurrence, negativity, and relative entropy of entanglement, for each state, quantifying the quantum correlations within each two-qubit system. Concurrence assesses the minimum resources needed to create an entangled state, while negativity indicates the extractable entanglement using local operations. This optimization, performed numerically, required meticulous techniques to ensure accurate results. The study then employed sophisticated statistical analysis, including bootstrap resampling and systematic data binning, to account for scatter and noise inherent in empirical quantum data. Researchers fitted the data to both exponential and polynomial models to rigorously test for saturation behavior in metrological advantage, a key prediction of quantum resource theory. Scientists generated 20,000 random two-qubit mixed states and systematically quantified both their entanglement, using concurrence, negativity, and relative entropy of entanglement, and their metrological capacity as measured by the MQFI. The research demonstrates that optimizing the MQFI through local unitary transformations yields substantially more predictable relationships than fixed-generator approaches, providing a clearer understanding of quantum metrological gain. Experiments revealed strong empirical correlations between entanglement measures and the MQFI, supporting the concept of saturation behavior in metrological advantage.

Data shows that exponential and polynomial fits provide robust quantitative models of this relationship. The team employed sophisticated statistical analysis, including bootstrap resampling and systematic data binning, to address the challenges of scatter and noise inherent in empirical quantum data, allowing them to reveal underlying functional relationships with high precision. Measurements confirm that the maximized quantum Fisher information effectively eliminates dependence on the choice of measurement generator, revealing the inherent metrological potential of each quantum state. The research establishes that the observed relationships are well-described by both exponential and polynomial functions, offering crucial guidance for the design of quantum sensors and the optimal allocation of quantum resources in realistic experimental conditions. These findings directly validate important predictions from quantum resource theory and set fundamental bounds for optimization and resource allocation in quantum sensing applications.

Entanglement and Metrological Capacity Empirically Confirmed

This research presents a comprehensive empirical analysis of the connection between entanglement and metrological capacity in two-qubit systems, systematically examining 20,000 randomly generated states. The team demonstrates strong positive correlations between three distinct entanglement measures, concurrence, negativity, and relative entropy of entanglement, and maximized quantum Fisher information, achieving exceptionally high accuracy with polynomial fits. Importantly, the analysis provides empirical support for saturation behavior in quantum metrological enhancement, confirming predictions from quantum resource theory and offering precise characterization of these limits. The study highlights the significance of optimizing measurement strategies, showing that local optimization to determine maximized quantum Fisher information yields far more predictable relationships than fixed-generator approaches. Furthermore, the research reveals that moderate levels of entanglement offer the best balance between sensing enhancement and resource requirements for practical applications, and that even separable states possess substantial metrological utility. The team confirms the robustness of these entanglement-metrology relationships under realistic decoherence conditions, particularly phase damping, strengthening their potential for real-world applications.