The study was approved by the local ethics committee of the medical Faculty of the University of Leipzig (026/18-ek), the study was also registered at Clinicaltrials.gov (NCT04230603). Written informed consent, including consent for publication, was obtained from all the patients. All methods were performed in accordance with the Declaration of Helsinki.
Ensuring compatibility between combinations
A machine learning pipeline can be viewed as comprising the following independent components: Data, Preprocessing, Model, and Cross-validation.
These components are independent in the sense that, to compare different variations of one component, the remaining components must be held constant. In this study, to isolate the effect of preprocessing, all other factors including data order, model state and cross-validation were held constant. In Table 1 we outline the checklist used to ensure consistency across each component. These prerequisites ensured that the only variable altered was the preprocessing combination. Consequently, if preprocessing A outperformed preprocessing B, we could be confident that the observed differences were solely due to the preprocessing methods, with no confounding variables influencing the results.
Sampling a small but representative dataset
First, we needed to create a small representative subset as follows:
-
1.
Randomly select 1% of data from each patient and each class.
-
2.
Apply Kolmogorov–Smirnov test (K-S test, α = 0.05) for every wavelength to confirm that the empirical distribution in the reduced subset does not differ significantly from the corresponding distribution in the full dataset, thereby establishing that the subset is distributionally representative.
-
3.
Repeat until distributions of all wavelengths are representative to the whole dataset. In most cases, less than 5 repetitions were needed.
Afterwards, for each preprocessing combination, corresponding preprocessing was performed on the selected small representative prototype. This way we ensured that the model received the same data in the same order, only the preprocessing was different.
Preprocessing
Pipeline
The preprocessing pipeline comprised the following sequential steps:
-
1.
Reading Hyperspectral Datacube and Ground Truth Mask. The initial step involved importing the hyperspectral data along with the corresponding ground truth mask, which provided reference labels.
-
2.
Scaling. This step scaled the data values, using Normalization or Standardization methods to ensure uniformity and better convergence of neural networks.
-
3.
Smoothing. Noise reduction was achieved through smoothing techniques.
-
4.
Filtering.Filtering processes like blood and light reflection filtering were applied to remove possibly harmful artifacts.
-
5.
Finally, for each annotated pixel we extracted 3D patches, which became the input samples for neural networks. Each patch was generated from a labeled pixel along with its neighboring pixels. Patch sizes in this work were 3 and 5, so the input shapes of the samples were (3, 3, 92) and (5, 5, 92).
Scaling
Scaling is important not only for bringing all features into a consistent range, which enhances convergence, but also for eliminating biases, such as these stemming from unique spectral characteristics of each patient. To address this, we employed feature scaling techniques. Based on previous research22, we selected two algorithms: Normalization (scaling to unit length) and Standardization (Z-score). Figure 2a presents the formulas for these scaling methods and illustrates how each scaling affects the spectra.
Preprocessing techniques. (a) Spectra examples before (left) and after scaling (Normalization in the middle, Standardization on the right). Note the differing scales on the y-axes. (b) Three modes of smoothing: 1D, 2D and 3D, where the purple areas represent the region being subjected to the smoothing process at once for the respective mode (1D, 2D or 3D), while the red areas highlight the window which would be applied pixel by pixel sequentially across the purple area. The datacubes’ axis proportions are drawn not to scale for clarity.
Smoothing
To reduce noise, we tried 1D (spectral), 2D (spatial), and 3D (both) smoothing on our datacubes as part of preprocessing pipelines. Figure 2b illustrates these different approaches within a hyperspectral cube, where the purple areas represent the region being subjected to the smoothing process at the same time for the respective mode (1D, 2D or 3D), while the red areas highlight the window applied pixel by pixel across the purple area. 1D smoothing is applied along the spectral dimension. 2D smoothing is applied spatially to each spectral band. 3D smoothing involves the simultaneous application of filters across both spatial and spectral dimensions.
Three filters were chosen for smoothing: Median Filter (MF), Gaussian Filter (GF) and Savitsky-Golay Filter (SGF)25, the use of which led to a significant improvement in14. MF replaces each pixel value with the median of neighboring values within a specified window size. GF, in contrast, applies a Gaussian function with a specific sigma value to weigh the neighboring spectral values. SGF was applied only with 1D smoothing.
The sigmas used for GF and window sizes used for MF for each dimension are described in Sect. 3.2.6. These values were selected based on a comparative analysis of spectra visualizations before and after the application of smoothing, ensuring the chosen parameters effectively modified the spectra while preserving essential structural details. SGF was applied with a window size of 9 and a polynomial order of 2, as these parameters yielded the best results in the study by Collins et al.14.
Filtering
During our research, it was shown that our models tended to misclassify pixels with reflected light, and to a higher extent — pixels with blood(Fig. 3a). The likely cause is that the blood spectra are similar to cancerous spectra, as shown in Fig. 3b.
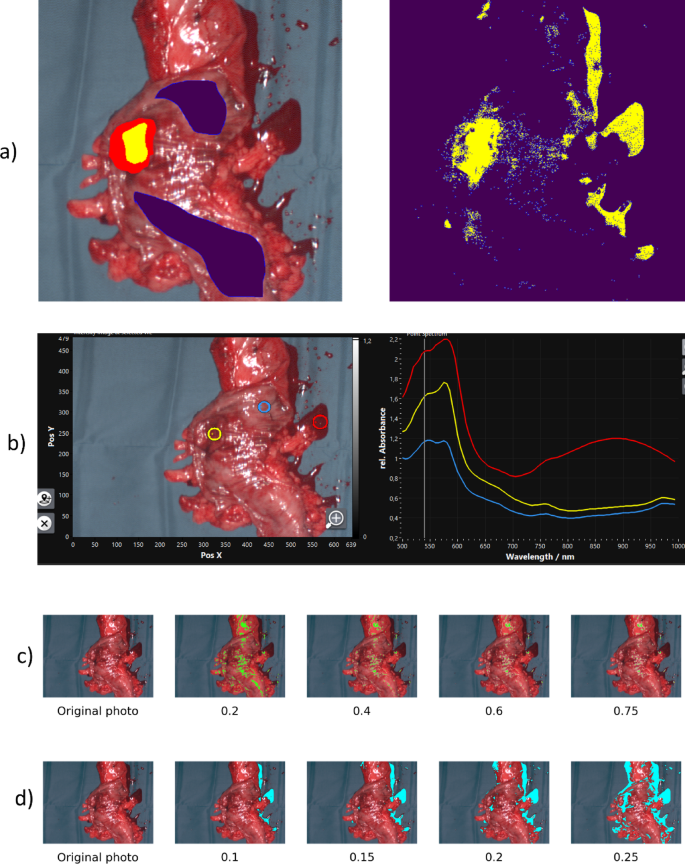
Filtering (a) Left: ground truth, note the blood. Right: prediction map that shows how blood is classified as cancer. Yellow shows cancerous tissues and violet non-malignant ones. (b) Screenshot from TIVITA Suite (Diaspective Vision GmbH, Am Salzhaff-Pepelow). The right picture shows spectra from the circled areas of the left picture, in the same colors. Blue is healthy tissue, yellow — cancerous tissue, red is blood. Note how the blood spectrum is much more similar to the cancerous spectrum than to the non-malignant. (c) Regions detected as reflected light (green) at different “light thresholds”. (d) Regions detected as blood at different “blood thresholds” are shown in cyan. Summary: blood spectra are more similar to cancer than to healthy tissue, explaining the high false‑positive rate and motivating blood‑pixel filtering.
Considering the above observations, we decided to exclude blood and light reflection pixels using the method for background extraction described in26 (Sect. 2.4). The background detection algorithm works by calculating three metrics — A, B, and C — from the hyperspectral image data. Metric A is the mean reflectance value over the wavelength range of 500 to 1000 nm, and metric B is the mean reflectance value within the 510 to 570 nm range. Metric C is a logarithmic function that compares the reflectance within the 650 to 710 nm range to a constant value. The pixel is classified as background, if A is less than 0.1, B is larger than 0.7, and C is negative. For clarity, in this work thresholds for these same A and B will be referred to as “light threshold” and “blood threshold”, respectively. In26, the light threshold was 0.1, and the blood threshold was set to 0.7. In this work, we tested different values for both thresholds to investigate effects on training outcomes. Figure 3c and d shows how many pixels were identified as light and blood for different threshold values.
Sample and class weights
With 477,670 cancerous and 4,537,769 non-malignant pixels, our dataset is imbalanced. To address this issue, we used class weights during training. Class weights are defined with the following formula:
$$class_weigh{t_{class~C}}=frac{{total~number~of~pixels}}{{number~of~pixels~of~class~C}}$$
Class weights are applied to the loss function. And in this case, for example, if cancerous tissue is misclassified, the loss function will be multiplied by class weight for cancerous tissue (~ 10 in our case). Hence, the ML model learns to pay more attention to the less represented classes.
In Fig. 1, it can be seen that the cancer area of the far-right patient is significantly bigger than the cancer area of the far-left patient. During previous research, it has been established that ML models perform better on patients who have bigger cancer areas, which seems reasonable, because patients with bigger cancer are more represented. But it is important to pay attention to the patients with smaller cancer areas as well, because each patient could contribute to a better generalization of the model. Therefore, we included sample weights in our tests. Sample weights are defined as:
$$sample_weigh{t_{class~C,~patient~P}}frac{{total~number~of~pixels}}{{number~of~pixels~of~class~C~of~patient~P}}$$
If sample weights were used, class weights were not used, because since sample weights are balanced through the total number of pixels, it means that all samples from all patients are already balanced.
The complete presentation of the tested combinations
In total, 1,584 combinations were tested for both patch sizes 3 and 5 (792 for each patch size). Figure 4 presents the preprocessing options that were permutated, such as Scaling (Normalization and Standardization), Smoothing (1D, 2D, and 3D with Median, Gaussian, and Savitzky-Golay filters), and filtering specific to blood and light characteristics. Smoothing options are parametrized with various window sizes and sigma values. Additionally, Sample Weights can be applied or omitted. This organized approach allows for systematic testing of different combinations to optimize data processing for subsequent analysis.
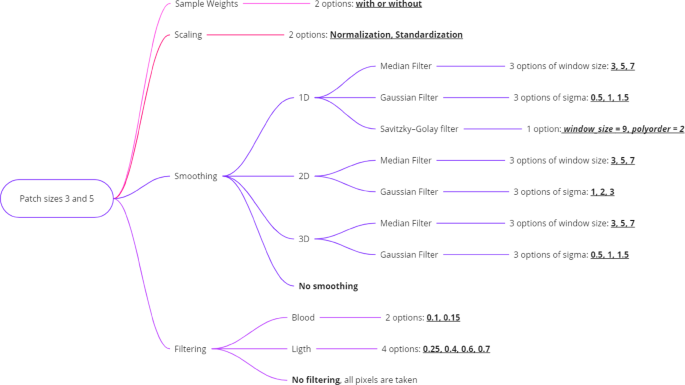
Flowchart depicting various preprocessing options for hyperspectral imaging data, including scaling, smoothing with multiple filters and settings, and filtering based on blood and light characteristics, starting from initial patch sizes of 3 and 5.
Training
Inception-based 3D-CNN architecture and cross-validation
Due to the limited dataset size (56 patients only), the decision was made to adopt pixel-wise classification, thereby increasing the number of samples, which is a common practice in medical imaging. This reframed the segmentation problem as an image classification task, for which the Inception model27 is particularly effective. That is the reason a 3D-CNN22 based on Inception was chosen. The initial architecture is depicted in Fig. 5a and incorporates a single block from the Inception architecture (designated by the gray rectangle). The Inception model offers numerous benefits, notably the concurrent utilization of multiple kernel sizes. This approach not only facilitates the integration of diverse feature maps but also reduces the likelihood of vanishing gradients. The use of ‘same’ padding in all convolutions ensures the preservation of dimensional consistency, facilitating seamless concatenation after each block.
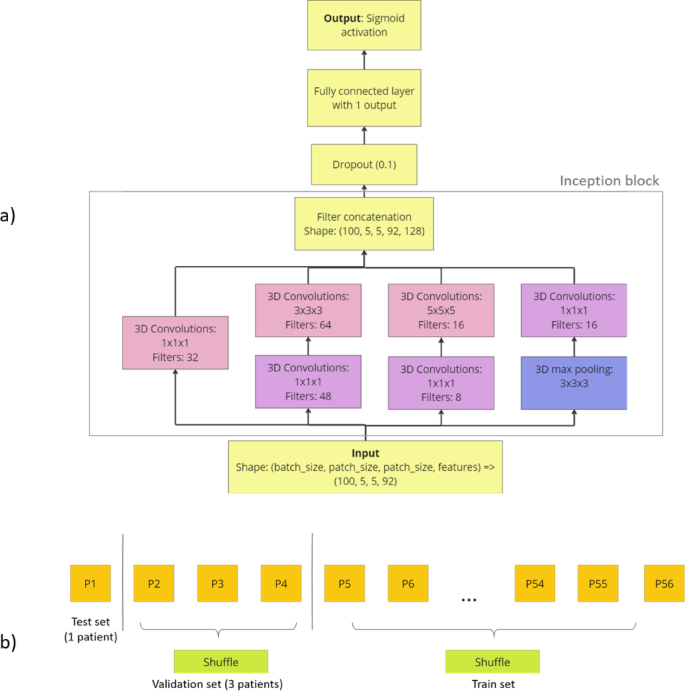
(а) Initial 3D-CNN Inception-based architecture. (b) The cross-validation used.
For each combination Leave-One-Out-Cross-Validation was performed. For our dataset of 56 patients, 56 folds were tested for each combination, where during each fold one patient was excluded as test set, three were used as validation set, the rest were used as train set. The described CV can be seen in Fig. 5b. Different numbers of validation patients were tested preliminary (1, 3, 10, 20), and three validation patients gave the best results.
Training parameters and infrastructure
Combinations were trained and evaluated with Python (3.7.4), Tensorflow (2.4.0) on the University Leipzig cluster with eight cores of AMD EPYC 32 core processor CPU and 2–8 RXT2080TI GPUs.
Training parameters:
-
Maximal epochs – 50.
-
Batch size – 500.
-
Loss – Binary cross-entropy.
-
Optimizer – Adam with β1 = 0.9 and β2 = 0.99.
-
Learning rate – 0.0001.
-
Activation – ReLU; last layer – Sigmoid.
-
Number of wavelengths – 92.
Early stopping was used to avoid overfitting: If the F1-score on the validation dataset did not improve for more than five epochs, training stopped.
Recommendations for implementation:
-
At least 16 RAM, possibly less with smaller batch sizes.
-
A processor with several cores would be a benefit.
-
At least one GPU would be a big benefit.
-
It is important to plan some time to implement parallel processing.
In our setup one combination needs 2–3 h to be trained on the small representative dataset. Training on the whole dataset needs 5–6 days, but with parallel processing it was reduced to ~ 1 day.
