Understanding the behaviour of complex quantum systems remains a central challenge in modern physics, demanding ever more powerful computational techniques. Peter Majcen, Giovanni Cataldi, and Pietro Silvi, alongside Simone Montangero and colleagues at the University of Padova, now present a significant advance in tackling this problem. Their research demonstrates a method for efficiently simplifying the calculations needed to model these systems, by focusing on the most important components of the quantum state. This optimisation dramatically reduces the computational resources required to simulate a range of models, including those relevant to particle physics and condensed matter systems, paving the way for more accurate and detailed investigations of quantum many-body phenomena.
Lattice Gauge Theory Simulations with Algorithms
This research focuses on developing and analyzing numerical methods for simulating quantum many-body systems, specifically those described by lattice gauge theories. These theories are crucial for understanding fundamental forces and phenomena like superconductivity and the behavior of quarks and gluons. The main challenge lies in the strong correlations between particles, making exact solutions difficult to find. Therefore, researchers employ sophisticated numerical techniques to approximate the behavior of these systems. The team combines techniques like exact diagonalization, k-side cluster mean-field theory, and tensor network methods to simulate lattice gauge theories.
They address the challenges of non-Abelian gauge symmetries by introducing a dressed-site formulation, simplifying the problem and creating a robust framework for studying strongly correlated systems. Exact diagonalization directly calculates the ground state of a system but is limited by computational cost. K-side cluster mean-field theory simplifies the problem by approximating interactions, offering a balance between accuracy and efficiency. Tensor network methods efficiently represent the wave function by exploiting the limited entanglement in many-body systems. Key concepts include matrix product states and density matrix renormalization group, which are well-suited for one-dimensional systems, and tree tensor networks for higher dimensions.
The entanglement area law justifies the use of tensor networks by linking entanglement to the area of a region’s boundary. The dressed-site formulation simplifies non-Abelian gauge symmetries by decomposing the parallel transporter, fusing degrees of freedom, and reducing the problem to an Abelian one while preserving locality. This approach utilizes the Gauss operator to enforce gauge symmetry, crucial for describing the strong force. The research builds upon concepts like the Hamiltonian, wave function, entanglement, gauge symmetry, and lattice gauge theory, providing a comprehensive framework for simulating complex quantum systems.
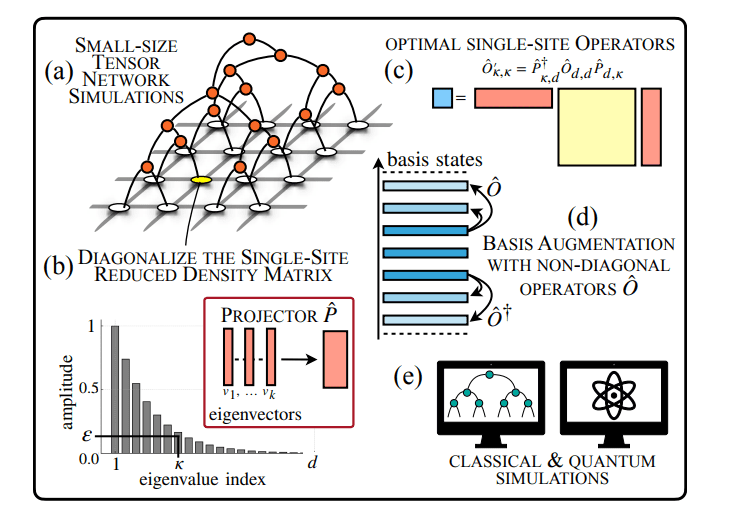
Optimal Truncation of Hilbert Space Achieved
Scientists have achieved a breakthrough in simulating complex quantum many-body systems by developing a method to optimally reduce the size of the local Hilbert space, a crucial step for both classical and quantum computations. This new approach leverages the single-site reduced density matrix, identifying and retaining only the most relevant states based on their corresponding eigenvalues. The team demonstrated that by accurately estimating the reduced density matrix using techniques like exact diagonalization, mean-field theory, and tensor networks, they could construct an optimal local basis for simulations. Experiments revealed that this pre-processing step allows for a substantial reduction in the computational cost associated with both classical and quantum simulations, as the dimension of the local Hilbert space directly impacts memory requirements and algorithmic complexity.
The method identifies the most important states, allowing researchers to discard less relevant ones without compromising the fidelity of the simulation. Measurements confirm that this technique is accurate and numerically stable across various model phases, even in scenarios approaching quantum phase transitions. The research successfully applied this method to diverse systems including the Sine-Gordon model, the φ⁴ theory, and lattice gauge theories with both Abelian U(1) and non-Abelian SU(2) symmetries in one and two spatial dimensions. This breakthrough delivers a versatile tool applicable to systems with large or infinite local Hilbert spaces, such as bosonic lattice models, lattice gauge theories, and electron-phonon systems, paving the way for more efficient and accurate simulations of complex quantum phenomena. This advancement promises to unlock new possibilities in materials science, condensed matter physics, and quantum computing.
Optimal Truncation of Hilbert Space Simplifies Simulations
This research presents a new method for reducing the computational complexity of simulating many-body quantum systems, particularly those relevant to particle and field theories. The team developed a technique to optimally truncate the local Hilbert space by focusing on the most important eigenvalues of the single-site reduced density matrix. This approach accurately represents the system’s behaviour while significantly reducing the number of variables needed for computation, improving both efficiency and numerical stability. The method’s effectiveness was demonstrated across a range of models, including scalar field theories in one and two dimensions and Abelian and non-Abelian lattice gauge theories.
Results indicate that the optimized basis is especially beneficial in phases where the system’s symmetry is broken, as these phases typically require much larger Hilbert spaces with conventional simulation methods. Importantly, the team showed that representing the system in a plaquette basis provides a more compact and efficient representation, particularly for lattice gauge theories. This advancement is especially valuable in the current era of noisy intermediate-scale quantum computing, where quantum resources are limited, and offers the most efficient encoding of local degrees of freedom on a quantum device. The authors acknowledge that the method relies on calculations performed on relatively small systems to estimate the reduced density matrix. Nevertheless, this research represents a significant step towards enabling more accurate and efficient simulations of quantum many-body systems, opening new avenues for exploring fundamental physics and developing novel quantum technologies.