Forelimb motion and reciprocation mediate aerodynamic control in a gliding lizard | BMC Ecology and Evolution

Study taxon and husbandry

Hemidactylus platyurus is an arboreal species with morphological adaptations that increase surface area (i.e., finger and toe webbing approximately one-third the length of the digits, ventrolateral skin folds on the trunk, and a dorsoventrally flattened tail; [23]). These adaptations likely act as basic airfoils [24] that enhance gliding performance [25] through decreased wing loading [26], although their aerodynamic function has been debated (see [20]). Individuals of H. platyurus have been observed falling with limbs outstretched [20] and documented to glide and have aerial control by using their tail as an inertial appendage to control pitch, roll, and yaw [17, 18, 27].

We used eight (5 male/3 female) adult flat-tailed house-geckos (H. platyurus) (mean body mass: 4.23 ± 0.92 g; mean SVL: 57.2 mm). All animals were acquired in June of 2018 from LLL Reptile. Geckos were housed in large mesh-walled tanks (width: 50.8 cm, length: 50.8 cm, height: 99 cm) within temperature-controlled rooms (24 °C) with a 12:12 h light:dark cycle. Each tank housed 4–5 individuals. All geckos were provided live crickets and water ad libitum. The ambient room temperature in which experiments were conducted was approximately 25 °C. All procedures were approved by the University of California, Berkeley Animal Care and Use Committee.

Experimental procedures

We used the same equipment and similar procedures as we used in previously published studies [13, 28] (see Fig. 1 in [13] for illustration). In lieu of dropping the lizards from elevated heights (e.g., [19, 25]), we simulated gliding through use of a custom vertical wind tunnel (Wind Generator 01–10, Aerolab, Laurel, MD, USA; see Supplementary Materials). Since air flowing past a relatively stationary animal is aerodynamically equivalent to an animal moving at the same speed through still air, such a simulation provides equivalent ensuing forces in the air (e.g., [15]). This method both reduced risk of animal escape and enhanced our ability to film (see Movies S1-S2). Due to interindividual variation in lizard mass, we adjusted the nominal windspeed for equilibrium gliding to each individual.

We filmed each aerial event at 400 frames per second using three synchronized cameras (HiSpec 1 cameras, Fastec Imaging, San Diego, California, USA); one camera was positioned at dorsal (top; 960 × 990 pixels; 25 mm lens) perspective and two cameras were positioned at lateral perspectives, both of which were elevated ~ 20° above horizontal (front and side; 1024 × 992 and 832 × 872 pixels, respectively; 50 mm lenses) so as to increase visibility of anatomical landmarks. Given the filming speeds, additional tungsten lighting was needed from above and the sides. As in [13] and [28] we calibrated the cameras in pairs by recording and later digitizing checkerboard points via stereo image pairs [29]. We used footage of a polystyrene ball (diameter of 4 cm, mass of 0.034 g) falling vertically through the test arena, along with a horizontal arena edge, to define the global coordinate system.

Immediately prior to each gecko recording, we recorded the individual’s mass, and then applied non-toxic, high-contrast landmarks at relevant anatomical positions to the gecko’s skin (Figs. 1 and 2) with dark eyeliner (Megaliner, Ulta Beauty) or white paint pen (Garden Marker 450, Monami). We thus marked 14 total landmarks (but see Supplemental Materials): midway between the pectoral and pelvic girdle (or midbody), tail tip and on the wrist, elbow, shoulder, ankle, knee, and hip on both the left and right sides.

We recorded glides for each of the 8 individual geckos fifteen times in the wind tunnel (i.e., 120 videos total). The duration of each recording ranged from 1–10 s. To begin a recording, the gecko was released by hand into the airflow at a height of approximately 25 cm above the arena’s floor. The recording was terminated within ~ 5 s of the start of a gliding event (i.e., traversing horizontally across any portion of the test section) or if the gecko halted its glide by either adhering to an arena wall or gripping the arena’s floor. The geckos did not always perform a gliding event or a limb reciprocation behavior of interest, so we only digitized a subset of all recorded sequences.

First, we identified those videos in which the gecko performed a gliding event. Among those videos, we removed any videos whereby the anatomical landmarks were not visible in at least 40% of frames or at the start and end of a gliding event in at least two cameras; a gliding event began when the gecko lost physical contact with the arena’s walls, floor, or with the researcher’s hand, and ended when the gecko regained contact with the arena. We then reexamined each of these gliding events and selected those recordings in which the geckos performed large and reciprocating forelimb motions relevant to our hypothesis. A total of 32 trials met these criteria from which we quantified limb and body motions. Among these 32 trials, points were visible in two cameras for an average of 95.6% frames.

Kinematics measurements

For each of the 32 trials, we identified the frames in which the gliding event occurred, and tracked anatomical landmarks using DLTdv7 point-tracking software in MATLAB (The MathWorks; [30, 31]) in all three cameras. We used a checkerboard calibration routine in MATLAB to calibrate the cameras; the mean reprojection error across all calibrations was 0.818 ± 0.44 mm. We only used two-camera pairs (i.e., front and side, front and top, and side and top) to triangulate the 3D coordinates for analysis because the cameras differed in frame size and two cameras provided sufficient positional characterization of landmarks. For each trial, we selected the camera pair with the lowest amount of landmark occlusion and the smallest digital reprojection error. Using the ‘triangulate’ function in MATLAB, we reconstructed the three-dimensional point coordinates of the digitized landmarks for the corresponding camera pair. We smoothed positional data with a quintic spline smoothing algorithm [32], adjusting the tolerance value for each trial according to fit using the ‘splinetool’ function in MATLAB. We used this function to interpolate positional data for frames in which landmarks were occluded and used the first- and second- derivatives of each spline to approximate the instantaneous velocity and acceleration, respectively [32]. We calculated roll and pitch of the body, as well as (for both the left and right sides of the gecko) the angles of shoulder retraction, shoulder adduction, elbow flexion, hip retraction, hip adduction, knee flexion, and of the tail relative to both the sagittal and frontal plane (summarized here; see Supplementary Materials and Fig. 2 for details) in all 32 trials so as to quantify overall aerial performance.

To characterize body orientations and limb angles through time, we used vectors between relevant landmarks and two virtual planes: (1) the chest plane, which was bounded by the left shoulder, right shoulder, and midbody, and (2) the abdominal plane, which was bounded by the left hip, right hip, and midbody. To calculate body roll, we found the midpoint between the shoulders (i.e., midshoulder) and created a vector between it and the midbody point. We computationally aligned this vector with the global x-axis and measured the angle between the resulting chest plane and horizontal, such that a roll to the gecko’s right was represented by a negative angle, and a roll to the left was positive. Likewise, to calculate body pitch, we aligned the shoulders with the global y-axis and measured the angle between the chest plane and horizontal; positive pitch angle represents nose-up pitch, and negative pitch is a nose-down orientation. Note, however, that the mid-body point was slightly dorsal to the shoulder points, so when the chest plane was parallel to the horizon, the gecko would exhibit a slightly positive pitch (pitch up); alternatively, if the gecko itself were parallel to the horizon, body pitch would be slightly negative. This observation means that pitch values are skewed slightly negative, which introduces a small error in calculations for which the chest plane was used.

We measured body bend at the midbody point by identifying the midpoint between the hips (midhip), projecting it onto the chest plane, and measuring the angle bound by these three points (with its vertex at midbody). We added 180° to this angle such that body bend angles less than 180° represent a flexed vertebral column (i.e., with hips below the chest plane), and angles more than 180° represent vertebral extension (i.e., with hips above the chest plane). We considered the tail angle on the frontal plane as the clockwise rotation of the tail about the mid-hip point, whereby an angle of 180° represents the directly posterior position and angles < 180° and > 180° represent right and left displacement, respectively. To calculate the angle of the tail in the sagittal plane, we determined the angle between the tail and the abdominal plane, whereby negative and positive angles are below and above the abdominal plane, respectively.

To estimate shoulder adduction angle, we calculated the angle between the humerus and the chest plane. Negative and positive angles represent ventral and dorsal positions, respectively. We computed the shoulder retraction as the angle between the line connecting the shoulders and the humerus, as projected onto the chest plane. A positive shoulder retraction angle represents an anterior position, and a negative angle represents a posterior position. Similarly, we used the left hip, the right hip, and the midbody to define an abdominal plane which we coordinated with the knee and the hip axes to calculate hip adduction and retraction. To estimate elbow flexion angles, we calculated the angle between the humerus and the vector defined by the elbow and the wrist for the right and left forelimbs. Similarly, we estimated knee flexion angles using the femur and the vector defined by the knee and ankle. Since shoulder and elbow actuation can both change hand position, we also quantified the position of the wrist relative to the shoulder using the same method as with shoulder retraction, but using the wrist instead of the elbow.

For velocity estimates, we used the x-, y-, and z-components of the midbody because it was the landmark nearest to the center of body mass (i.e., approximately midway between the forelimbs and hindlimbs; see [33]). Vertical speed was taken to be the z-component of the body velocity. To calculate horizontal speed, we used the square root of the sum of the squares of the x- and y-components, which we then used to calculate forward speed, defined here as the horizontal speed in the direction of the gecko’s body axis such that a positive forward speed was in the gecko’s cranial direction. We estimated glide angle as the angle between the vertical speed and the horizontal speed, and considered forward speed, vertical speed, and glide angle to be the primary measures of glide performance. Similarly, we used the x-, y-, and z-components of midbody acceleration to calculate analogous acceleration values.

Aerial postures and limb retraction

Since the kinematic focus of this study was on the novel behavior whereby geckos carried out symmetric and large-amplitude limb motions, we used Pearson correlation tests to detect bilaterally symmetric patterns in limb movements to decide which trials should be used for more detailed analyses, and to characterize gliding postures, detailed below as “skydiving” and “swept configuration” (see Fig. 1; Table 1). A limb motion was considered bilaterally symmetrical if the left and right sides showed a significant and positive correlation for that motion (e.g., shoulder retraction angle). Although we observed that the forelimb motions were far more dramatic than those of the hindlimbs, we nonetheless tested for bilateral symmetry between the left and right hip angles in each of the 32 trials. Whereas many of the trials demonstrated correlations between the left and right side for both the retraction and adduction angles, the signs of those movements were inconsistent and resulted in similar proportions of symmetrical and asymmetrical movements (Table 2). Since we were specifically interested in characterizing symmetric limb movements in this study, we did not further detail hindlimb kinematics.

For the forelimbs, the change in shoulder retraction angle was noticeably more dramatic than that of the shoulder adduction angle (Movie S1-S2; Table 1). Thus, we only tested for bilateral symmetry between the left and right shoulder retraction angles (Table 2), opting to instead include shoulder adduction angle as a dependent variable in downstream analyses. Shoulder retraction angles were significantly and positively correlated (p > 0.004 in all cases), with correspondingly symmetrical movements, in only 24 of 32 trials. Of these, we used only those trials in which at least one of the shoulders moved through a retraction angle of at least 45º, thus eliminating all trials in which the shoulder retraction angles were either small or not positively correlated (i.e., not symmetrical) for detailed characterization of the forelimb retraction behavior. 20 trials were thus identified further kinematic analysis (Table 2). We used limbs from only one side per trial for analysis, selecting the side for which the forelimb was more representative of the retraction behavior (e.g., moved through a greater angle). In total, we analyzed 12 right forelimb sweeps and 8 left forelimb sweeps (Table 3).

We considered the starting point for forelimb sweep to be either the local minimum immediately prior to large-amplitude shoulder retraction (Figure S1) or the first recorded frame. The end of forelimb sweep was defined as the first local maximum following shoulder retraction. We calculated the sweep amplitude as the difference between retraction angles at the start and at the end of this behavior. The half-period of the behavior was calculated as the difference in time between its start and end.

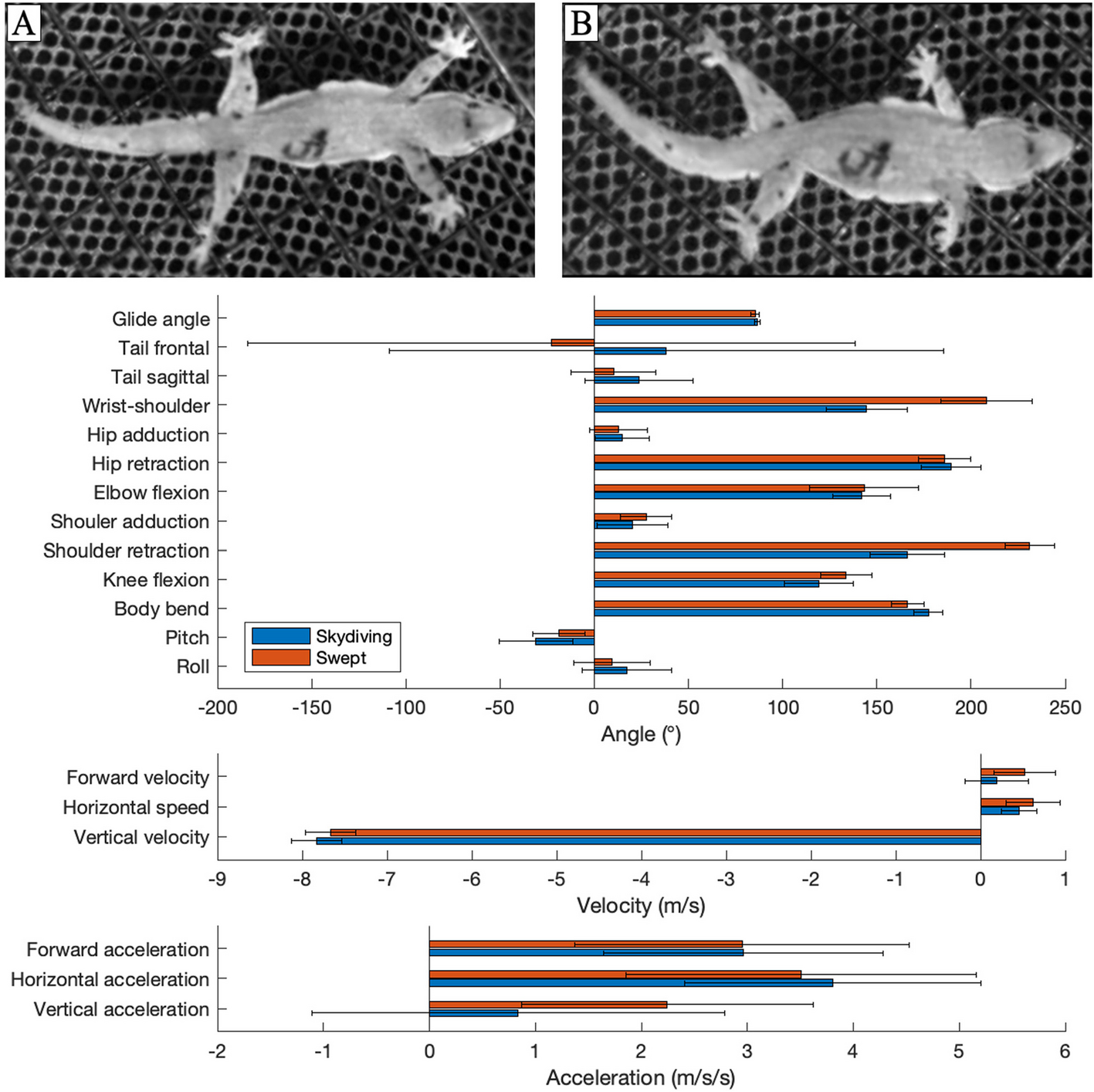
Qualitative observation suggested that large-amplitude shoulder retraction enabled transition between two primary gliding postures that we thereafter referred to as “skydiving” and “swept configuration”. The skydiving posture is comparable to that previously described in the literature [19, 21], with the body and tail flattened and the limbs laterally extended. Here, we distinguish the skydiving posture from the swept configuration primarily by the position of the forelimbs. Qualitatively, the forelimbs are held in a protracted (anterior) position in the sky-diving posture, whereas in the swept configuration, the forelimbs are retracted posteriorly. We used the single frame in which the local minimum marking the start of the shoulder sweep for the skydiving posture, and the local maximum for the swept configuration (Figure S1). At each of these timepoints, we characterized overall posture of the geckos by determining mean values of the pose variables among the trials (Table 1; Fig. 2). We then compared mean values for each of these variables using paired t-tests between skydiving and the swept configuration if the variable was normally distributed (determined by Lilliefors test; Table S1), or with a Wilcoxon signed-rank test if not (Table 1).

Variation in forelimb behaviors

Behavioral variation in forelimb retraction was evident among trials (see Table 3). In nine of 20 trials, geckos performed a recovery stroke before the end of data collection, whereby the limbs exhibited substantial protraction towards the skydiving position (assessed visually, e.g., Figures S2-S3; Table 4). In all of these trials, the limbs returned to within 36% of each particular trial’s sweep amplitude relative to the initial retraction angle, as measured at a local minimum after the sweep or at the last frame of data. From these data, we determined the sweep duration. We characterized the posture at the end of the recovery stroke with the same measurements as were used for the skydiving and swept configuration postures. For these nine trials, we performed a repeated-measures ANOVA and Tukey–Kramer posthoc-analyses to compare the skydiving posture, swept posture, and “recovery” postures if the variable was normally distributed (determined by Lilliefors test; Table S1), or with a Friedman test and Dunn’s posthoc analyses if not (Table 4).

Occasionally, the gliding event was long enough to capture multiple shoulder retractions. Only two trials (gecko 3: trial 9 and Gecko 5: trial 10B) included two clear local maxima (e.g., Figure S1) indicative of the end of limb retraction. In addition to these trials, we analyzed three trials that captured a full sweep and also a sweep segment wherein the local maximum occurred prior to the onset of data collection, but for which the included data were greater than the local maximum used to define the sweep (e.g., Figure S2). Whereas this approach does not capture the entire behavior (and thus overestimates the effective reciprocation frequency), it does demonstrate the frequency at which the gecko could potentially sweep its arm from the maximum value to the minimum and then back to the maximum. The inverse of this period of sweeping motion was assumed to indicate such a potential reciprocation frequency.

In some trials, the gecko did not return their forelimbs to the skydiving position after the sweep either immediately (or at all), but instead oscillated the shoulders with low-amplitude changes in retraction angle (see Figure S1). We defined occurrence of this behavior as when trials showed a local minimum in shoulder retraction after the sweep, but either before a return to the skydiving position or with no such return. This behavior occurred for at least one cycle in 14 of 20 trials. As with forelimb sweeps, we recorded the amplitude and half period of these displacements, but we used the local maximum and minimum positions to indicate the start and end of the behavior, respectively.

Statistical analysis

We performed Pearson correlation analyses between shoulder retraction angle and adduction angle. We also performed cross-correlation tests [34] in RStudio [35, 36] to identify relationships between the postural variables of shoulder retraction angle, pitch, and body bend (Table S2). For each of these postural variables, we performed cross-correlations with tail angle in the sagittal plane, forward velocity, vertical velocity, forward acceleration, and vertical acceleration (Tables S1-S2), so as to identify relationships between them while taking into account potential time lag between series (see [10]). Briefly, cross-correlation tests evaluate relationships between potentially lagged time series by staggering data incrementally across a variable number of time steps, and then generating correlation coefficients for each time step and corresponding lag (negative and positive lag values indicate that series 2 is shifted backwards or forwards in time, respectively, relative to series 1). However, because the relationships of interest were those of limb posture on glide performance, we only identified the positive lag for the closest and highest coefficient relative to zero lag. Finally, we performed a Pearson correlation test on the lagged dataset (see Fig. S4).