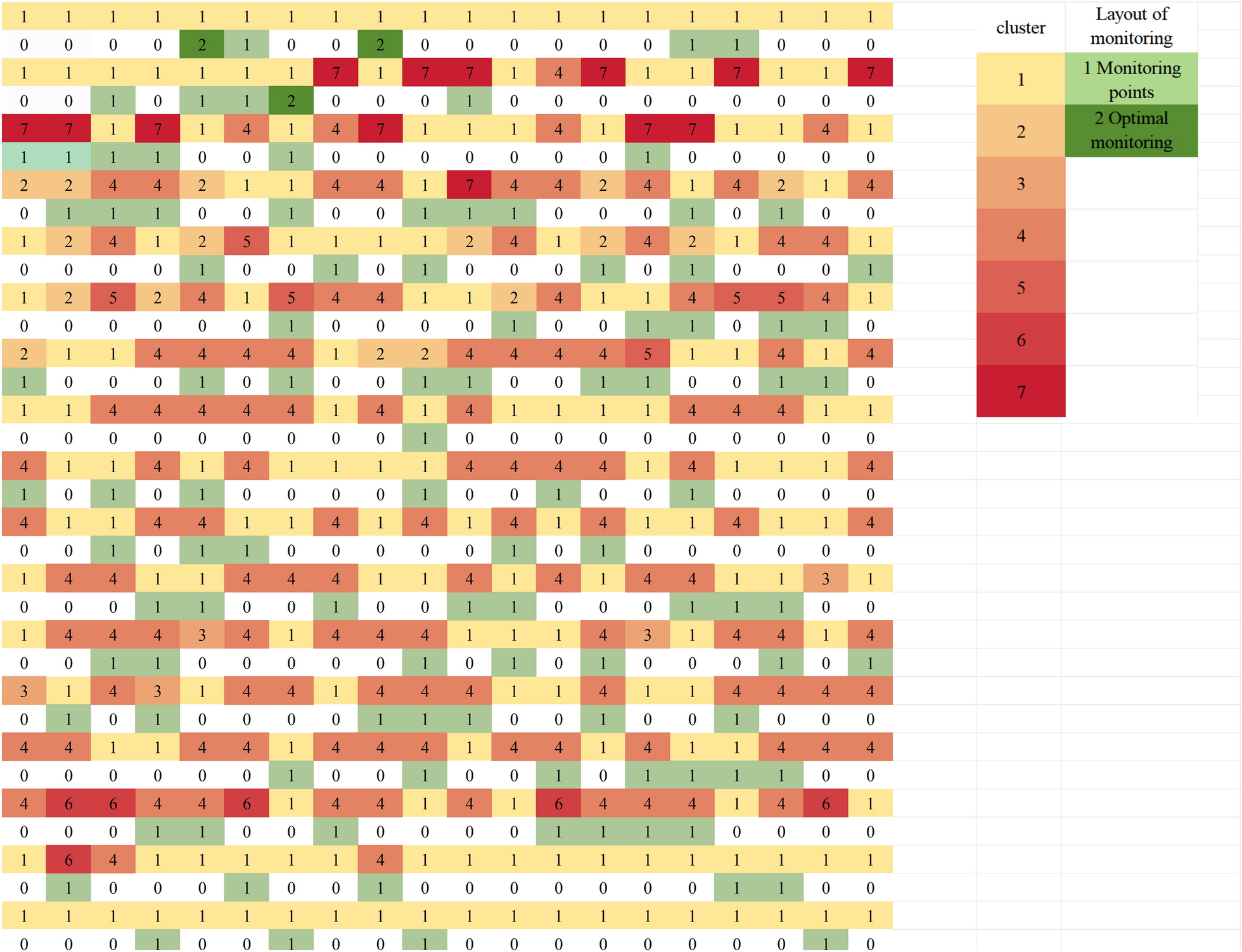
Design process of the monitoring network
A spatial cluster stratified sampling (SCSS) approach was developed for the design of the monitoring network, which includes four steps: (i) Determine cluster stratification, (ii) Determine the optimal sample size, (iii) Select representative sample cities, and (iv) Evaluating spatiotemporal representativeness (Fig. 1). Using HFMD incidence data from 2018, we selected representative sample cities from 340 cities to form the monitoring network. We then evaluated these cities based on how well they represented the unselected ones. To verify the stability of the representativeness of this monitoring network, we conducted a sensitivity analysis using data from 2019.
Flowchart of monitoring network design procedures. In the figure, SKATER stands for Spatial Kluster Analysis by Tree Edge Removal
All statistical analyses were two-sided, conducted with a significance level of 0.05 (α = 0.05), using R (version 4.3.2; R Foundation for Statistical Computing, Vienna, Austria).
Determination of clustering stratification
We calculated the Calinski-Harabasz (CH) index, which measures the ratio of between-cluster to within-cluster variance, and selected the optimal number of clusters yielding the highest CH value [21, 22]. However, in high-dimensional settings (e.g., monthly scale data with 12 features), ensuring sufficient intra-cluster sample size is critical to avoid unreliable clustering outcomes. Specifically, when the sample size within a cluster is smaller than the data dimensionality, the clustering process may become unstable and prone to overfitting, capturing noise rather than meaningful patterns [23]. To address these challenges, we established a constraint on the maximum cluster number (kmax) to guarantee that the average intra-cluster sample size exceeds the number of dimensions (d = 12). The optimal number of clusters within each region was then determined using the CH index, with the range of possible clusters set from 1 to kmax. The formula for this constraint is kmax = ⌊N/d⌋. Applying this to China’s 340 prefecture-level cities (N = 340) with a feature dimensionality of d = 12, the maximum cluster number kmax is determined by the ratio kmax = ⌊N/d⌋ = ⌊340/12⌋ = 28. If further hierarchical clustering is needed, the same formula can be applied iteratively to determine the maximum number of sub-clusters at each subsequent level, ensuring methodological consistency. We then used Spatial Kluster Analysis by Tree Edge Removal (SKATER) with first-order edge adjacency of spatial polygons as the constraint to stratify the data based on the optimal number of clusters. SKATER is a spatially constrained clustering algorithm that partitions spatial data into homogeneous groups, considering both similar attribute values and spatial contiguity, by incrementally removing edges from a minimum spanning tree [24].
Determination of the sample size
After determining the number of strata, the sample size for each stratum was calculated using the Neyman method [25], and simple random sampling was then conducted within each stratum 100 times, with overall sample sizes ranging from 20 to 320 in increments of 10. We plotted a curve of average root mean square error (RMSE) against sample size, where the RMSE was calculated from the difference between the predicted incidence rates, obtained through Ordinary Kriging interpolation with a Spherical semivariogram at unselected cities, and the actual values. The absolute value of the derivative was calculated based on the change in RMSE with varying sample sizes, representing the sensitivity of RMSE improvement to changes in sample size. We selected the sample size corresponding to an absolute derivative value of 1, as adding one more city beyond this point would only reduce the RMSE by less than 1/100,000. This implies that further increases in the sample size would no longer significantly improve accuracy [26, 27].
Selection of representative sample cities
We performed 100 samplings based on the sample size determined in the previous step and selected the plan with the minimum RMSE from them. Subsequently, we applied cyclic optimization to finalize the monitoring network. The specific process is as follows: (i) We calculated the Spearman’s rank correlation between the true and predicted weekly incidence rates for each city. (ii) Cities with non-significant correlations (P > 0.05) were identified. These cities were poorly predicted by the existing monitoring network and thus needed to be added to enhance monitoring effectiveness. (iii) After incorporating these poorly predicted cities into the monitoring network, we utilized the updated monitoring network to perform Kriging interpolation and generate new predicted incidence rates. (iv) Based on these updated predictions, we recalculated the Spearman’s rank correlation for all cities. This process was repeated iteratively. In each iteration, new cities with non-significant correlations were identified and added to the network. The stopping criterion was met when all cities exhibited a significant correlation (P < 0.05) between their true and predicted weekly incidence rates.
Evaluation of spatial and temporal representativeness
For overall evaluation, the RMSE and Spearman’s rank correlation coefficient were used to assess the mean bias and correlation between the predicted and true annual incidence rates across all cities.
For spatial feature evaluation, the consistency of global Moran’s I between the predicted and true values was assessed. The consistency of hotspot regions was evaluated using the sensitivity, specificity, and accuracy indices for the predicted local Getis-Ord G* values, with the true values serving as the gold standard [28].
For temporal feature evaluation, Spearman’s rank correlation coefficient was used to assess the correlation between the predicted and true weekly incidence rates for each city. The annual percent change (APC), average annual percent change (AAPC), joinpoints, and their 95% confidence intervals (CI) from Joinpoint regression were compared between the true and predicted values. The comparison focused on whether the number of joinpoints was consistent and whether the 95% CI for the predicted APC, AAPC, and locations of joinpoints included the corresponding true values. The consistency in the number and location of joinpoints reflects the ability to identify critical time points for changes in disease information. Consistency in APC reflects the ability to identify short-term trend changes, while consistency in AAPC evaluates the ability to capture the long-term trends in directions and magnitudes [29].
Comparison of SCSS with the conventional methods
The conventional methods included K-means, traditional stratified sampling, and simple random sampling. The number of clusters and sample sizes of these conventional methods were the same as those used in the SCSS method. The K-means stratified sampling method included stratifying based on the results of K-means clustering, followed by simple random sampling within each stratum. Traditional stratified sampling divided the samples into eastern, central, and western regions, according to the standards of the National Bureau of Statistics [30]. Within each region, the samples were further stratified into high, medium, and low categories based on incidence rates. We compared the distribution of RMSE across SCSS, K-means, traditional stratified sampling, and simple random sampling over 100 iterations. A lower RMSE signifies more accurate predictions, while a more centralized RMSE indicates greater stability of the method.