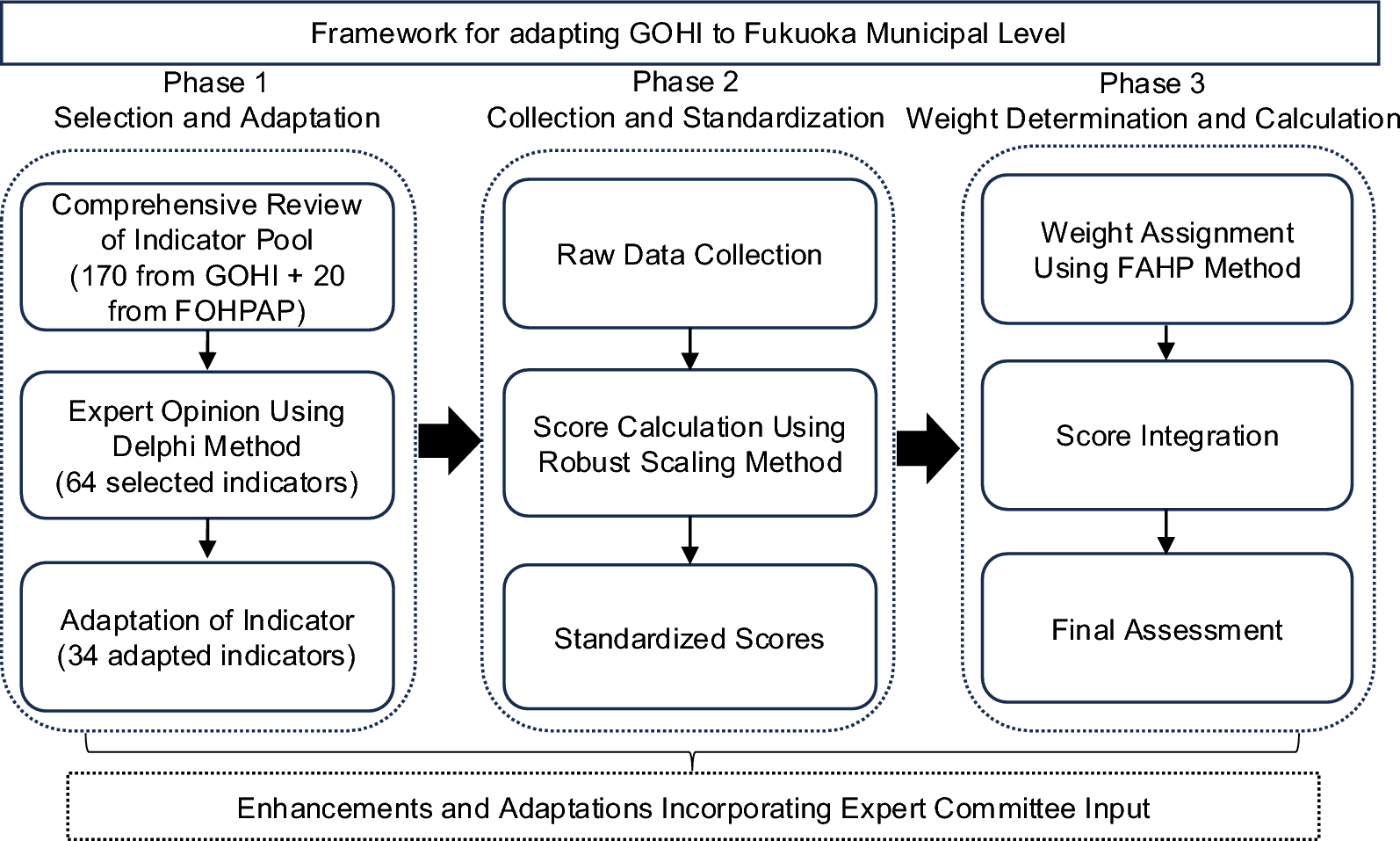
The research design framework of adapting GOHI to Fukuoka municipal level for constructing FOHI consists of three phases: Phase 1 (Indicator Selection & Adaptation), Phase 2 (Data Collection & Score Standardization), and Phase 3 (Weight Determination & Score Calculation) (Fig. 1).
Flowchart of GOHI Adaptation for Construction of FOHI. GOHI Global One Health Index, FOHPAP Fukuoka One Health Promotion Action Plan, FAHP Fuzzy Analytic Hierarchy Process
Phase 1: indicator selection and adaptation
In Phase 1, we began with a thorough review and analysis of the comprehensive pool of both GOHI 170 sub-indicators and 20 measurable indicators from FOHPAP [13,14,15, 25]. The GOHI sub-indicators were evaluated based on selection criteria (Table 1). Data and information were thoroughly searched, reviewed, and assessed from the following sources: e-Stat (Comprehensive portal site for Japan government statistics), FOHPAP, Fukuoka Prefectural One Health portal site, Fukuoka One Health Official Annual Reports, Fukuoka Prefecture website, and Fukuoka Prefecture open data site. [25, 33,34,35,36,37].
The initial selection of potentially suitable indicators was made from the GOHI and FOHPAP indicator pool. Indicators were finally determined from these initially selected indicators based on multiple expert consultations and validation using the Delphi method, which is a structured forecasting technique that gathers expert opinions, refining responses iteratively to achieve consensus [38].
Phase 2: data collection and standardization
In Phase 2, we collected data from the sources listed in Table 2. Most indicators were derived from national and Fukuoka Prefectural Official databases, supplemented by internal data obtained from the Fukuoka Prefectural Office.
The collected data for each indicator underwent rigorous standardization using the robust scaling method to address the heterogeneous nature of municipal-level data and potential outliers [53, 54]. This initial transformation centers the data around the median and scales it based on the interquartile range. The data was then linearly re-scaled to a uniform 0–100 scale for score standardization, while maintaining the relative relationships between municipalities.
Only two indicators had missing values. For the indicator A1.2 in Table 6, there are 32 water quality data monitoring points in 17 municipalities in Fukuoka prefecture. Therefore, the mean value from these 17 municipalities were imputed for missing in the remaining 43 municipalities. For the indicator C5.3 in Table 6, there are only 12 municipal observational monitoring sites. Therefore, the same imputation method as the indicator A1.2 was used for the indicator C5.3.
The robust scaling method is expressed by Eq. (1):
$$begin{array}{c}{X}_{text{scaled}}=frac{X-{text{median}}left(Xright)}{{text{IQR}}left(Xright)}times 100#end{array}$$
where X represents the original value, median(X) is the median of the indicator across all municipalities, and IQR(X) is the interquartile range. This transformation centers the data and scales it based on the interquartile range, making it less sensitive to extreme values. After this, we designated the highest observation value (ranked first among all 60 municipalities) as the optimal value, and the lowest observation value (ranked last among all municipalities) as the worst value to be standardized. We then linearly re-scaled the standardized data to ensure each indicator’s score falls within a uniform range of 0–100 points. For indicators where higher values indicate poorer performance, we applied reverse scoring after standardization to maintain interpretive consistency, ensuring higher scores uniformly represent better performance across all metrics. We deliberately avoided applying Min–Max normalization directly to the raw data as used in GOHI, as such an approach is susceptible to distortion from extreme outliers [55]. Instead, we first applied robust scaling to reduce the influence of outliers before performing the Min–Max normalization as a second step on the already robust-scaled data. For binary indicators (Yes/No), we assigned scores of 100 and 0 respectively. For ordinal indicators, we applied proportional scoring (e.g., 0, 33.3, 66.7, and 100 for the four levels). For temporal consistency and data reliability, we established 2022 as our baseline year, aligning with the implementation of the FOHPAP. To address missing data points, we conducted multiple imputation procedures using contextually relevant variables identified through rigorous expert consultation processes.
Phase 3: weight determination and score calculation
In Phase 3, we determined “weighing” for each 3 categories and 13 key indices using the Fuzzy Analytic Hierarchy Process (FAHP), which incorporates fuzzy logic to handle uncertainty and imprecision in decision-making by using fuzzy pairwise comparisons to derive more reliable priority weights [56]. Equal weights were assigned to the 34 different measurement indicators within the same key indicator, according to the consensus from 23 One Health experts (Table 2). All 23 experts participated in a questionnaire survey which included 23 series of pairwise questions to compare “which of 3 categories and 13 key indices are more important”. Based on the results of each pairwise question, the relative importance of 3 categories and 13 key indices were determined at different hierarchical levels. Results from expert evaluations were systematically collected through repeated pairwise comparisons for each pair of indicators from 23 experts, transforming qualitative judgments into quantitative ratios [57].
To systematically aggregate the binary judgments from all experts, we constructed fuzzy judgment matrices for each hierarchical level. For each pairwise comparison between indicators i and (j), we counted the number of experts who preferred indicator (i) over indicator (j), denoted as ({a}_{ij}). This value could range from 0 to 23, reflecting the strength of collective expert preference. The reciprocal relationship between matrix elements was maintained as ({a}_{ji}) = 23/({a}_{ij}), ensuring mathematical consistency in the preference structure. This approach effectively converted binary judgments into a quantitative framework that captured both the direction and strength of collective expert preferences.
The aggregated judgment matrices were constructed at multiple hierarchical levels: (1) a top-level matrix comparing the three main categories (EDI, IDI, CDI), (2) a matrix for the five key indices within EDI, (3) a matrix for the three key indices within IDI, and (4) a matrix for the five key indices within CDI. For each matrix, we calculated the Consistency Ratio (CR) to verify judgment consistency. The CR values were 0.026, 0.081, 0.068 for the top-level, EDI, and IDI matrices respectively, all well below the strict threshold of 0.1, while the CDI matrix had a CR value of 0.131, which exceeded the stringent standard but remained below the secondary threshold of 0.15. This indicates that expert judgments maintained satisfactory consistency across all hierarchical levels, with most matrices demonstrating high consistency under the rigorous criterion.
The weight vector for each level was calculated using the geometric mean method, which is particularly suitable for fuzzy hierarchical analyses due to its ability to minimize the influence of extreme values and maintain ratio scale properties. For each indicator (i), the weight was calculated as:
$${W}_{i}=frac{{left(prod_{j=1}^{n} {a}_{ij}right)}^{1/n}}{sum_{k=1}^{n} {left(prod_{j=1}^{n} {a}_{kj}right)}^{1/n}}$$
where ({W}_{i}) represents the normalized weight of indicator (i); ({a}_{ij}) represents the fuzzy preference value of indicator (i) over indicator (j) (transformed to a 0–1 scale by dividing by the total number of experts); (n) is the total number of indicators being compared.
This weighting methodology was applied across all hierarchical levels of our assessment framework. For the system component level, the comparisons revealed varying degrees of relative importance. The final One Health performance score for each municipality was calculated through a hierarchical aggregation process that integrates the standardized indicator scores with their corresponding FAHP-derived weights. The calculation follows a bottom-up approach, progressively combining scores from the 34 measurement indicators to 13 main indices, and finally to the three index categories.
$$KI=sum ({X}_{i}times {w}_{i})$$
where ({X}_{i}) represents the standardized score for measurement indicator (i), and ({w}_{i}) represents its corresponding weight derived from the FAHP process. Based on expert recommendations, measurement indicators under the same Key Indicator were assigned equal weights in this study.
The Category scores (CS) are then computed by aggregating their respective Key Indicators:
$$CS=sum (K{I}_{j}times w{k}_{j})$$
where (K{I}_{j}) represents the score of Key Indicator (j), and (w{k}_{j}) represents the weight assigned to that key indicator within its category.
Finally, the overall One Health score (OHS) for each municipality is calculated by combining the three Categories:
$$OHS=(EDItimes {w}_{1})+(IDItimes {w}_{2})+(CDItimes {w}_{3})$$
where EDI, IDI, and CDI represent the scores for the External Drivers Index, Internal Drivers Index, and Core Drivers Index respectively, and w₁, w₂, w₃ represent their corresponding weights in the overall assessment framework. This hierarchical aggregation ensures that the final score reflects both the relative importance of different components and their interconnected relationships within the One Health system.
Final analysis and assessment
After calculating One Health scores for 60 municipalities in Fukuoka Prefecture, we employed various statistical methods to analyze the distribution of these scores. Common statistical approaches including descriptive statistics, box plots, and violin plots were utilized to examine the overall level of One Health governance and internal variations across the prefecture. Beyond standard statistical methods, we constructed spatial distribution maps of the scores and created bar charts of the top 20 municipalities in each of the three index categories. These additional analyses enabled a more detailed examination of regional differences, assessed the applicability of our indicator system at the municipal level, and provided scientific evidence for developing strategies to enhance One Health performance throughout Fukuoka Prefecture.
Additionally, we employed Latent Class Analysis (LCA) [58] to identify different One Health performance patterns among 60 municipalities in Fukuoka Prefecture. This analytical approach was guided by our hypothesis that geographically neighboring municipalities might exhibit similar patterns in One Health performance due to various forms of inter-municipal influence, including knowledge sharing, policy diffusion, shared environmental conditions, and collaborative initiatives. We assumed that each municipality belongs to one of n latent classes based on their scoring patterns across the three core indices: EDI, IDI, and CDI. To facilitate the analysis, we categorized the scores of these three core indices into four distinct score groups; “below 40.01,” “40.01–50,” “50.01–60,” and “above 60” as shown in Fig. 2. Using a data-driven approach, LCA determined the number of existing latent classes based on the distribution patterns of municipalities across the three core indices’ score groups. The analysis also calculated the posterior probability of each municipality belonging to each latent class, with the class having the highest posterior probability considered as the municipality’s latent class membership. The optimal number of latent classes was determined by the model with the lowest Bayesian Information Criterion (BIC) value among models containing 2–6 latent classes.
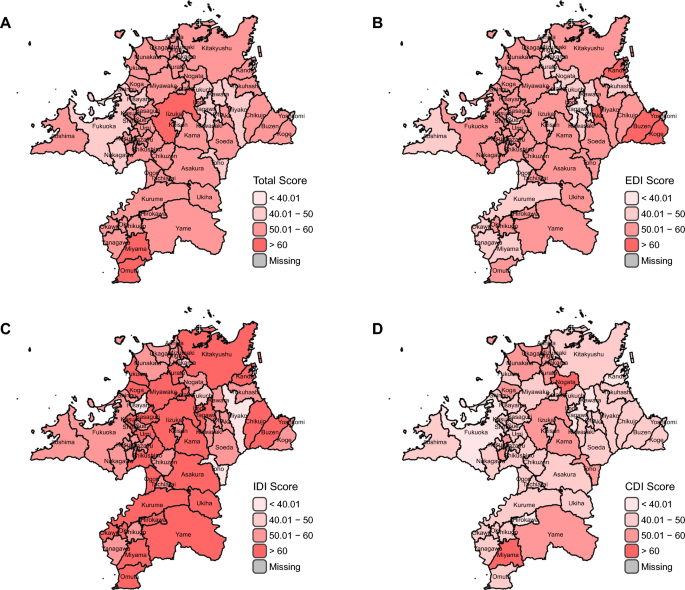
FOHI Scores among 60 municipalities in Fukuoka by Total A, EDI B, IDI C, and CDI D categories. Created based on National Land Numerical Information (Administrative Boundary Data), Ministry of Land, Infrastructure, Transport and Tourism, Japan (https://nlftp.mlit.go.jp/ksj/gml/datalist/KsjTmplt-N03-2025.html), retrieved on November 15, 2024. FOHI Fukuoka One Health Index, EDI External Drivers Index, IDI Internal Drivers Index, CDI Core Drivers Index
All statistical analyses and data visualizations were performed using R software version 4.2.1 (R Foundation for Statistical Computing, Vienna, Austria) [59]. The hierarchical fuzzy analytic hierarchy process (FAHP) was implemented using custom R scripts based on the algorithm described in the method section. Weight calculations, consistency ratio evaluations, and matrix manipulations were performed using the base R functions. For data visualization, the ggplot2 package [60] was utilized to create figures displaying weight distributions and comparative analyses across municipalities.