Ezzati M, Lopez AD, Rodgers A, Hoorn SV, Murray CJL, Group CRAC. Selected major risk factors and global and regional burden of disease. Lancet. 2002;360:1347–60.
PubMed
Google Scholar
SAMHSA. Results from the 2011 National Survey on Drug Use and Health: summary of national findings. NSDUH Series H-44, HHS Publication No (SMA) 12-4713. Rockville, MD: Substance Abuse and Mental Health Services Administration; 2012.
Google Scholar
Grant BF. Age at smoking onset and its association with alcohol consumption and DSM-IV alcohol abuse and dependence: results from the national longitudinal alcohol epidemiologic survey. J Subst Abuse. 1998;10:59–73.
CAS
PubMed
Google Scholar
Hu T, Gall SL, Widome R, Bazzano LA, Burns TL, Daniels SR, et al. Childhood/Adolescent smoking and adult smoking and cessation: the international childhood cardiovascular cohort (i3C) consortium. J Am Heart Assoc. 2020;9:e014381.
PubMed
PubMed Central
Google Scholar
Ziedonis D, Hitsman B, Beckham JC, Zvolensky M, Adler LE, Audrain-McGovern J, et al. Tobacco use and cessation in psychiatric disorders: National Institute of Mental Health report. Nicotine Tob Res. 2008;10:1691–715.
PubMed
Google Scholar
Choi WS, Patten CA, Gillin JC, Kaplan RM, Pierce JP. Cigarette smoking predicts development of depressive symptoms among U.S. adolescents. Ann Behav Med. 1997;19:42–50.
CAS
PubMed
Google Scholar
Wu LT, Anthony JC. Tobacco smoking and depressed mood in late childhood and early adolescence. Am J Public Health. 1999;89:1837–40.
CAS
PubMed
PubMed Central
Google Scholar
Goodman E, Capitman J. Depressive symptoms and cigarette smoking among teens. Pediatrics. 2000;106:748–55.
CAS
PubMed
Google Scholar
Ranjit A, Buchwald J, Latvala A, Heikkilä K, Tuulio-Henriksson A, Rose RJ, et al. Predictive association of smoking with depressive symptoms: a longitudinal study of adolescent twins. Prev Sci. 2019;20:1021–30.
PubMed
PubMed Central
Google Scholar
Baiden P, Szlyk HS, Cavazos-Rehg P, Onyeaka HK, Peoples JE, Kasson E. Use of electronic vaping products and mental health among adolescent high school students in the United States: the moderating effect of sex. J Psychiatr Res. 2022;147:24–33.
PubMed
Google Scholar
Johnson JG, Cohen P, Pine DS, Klein DF, Kasen S, Brook JS. Association between cigarette smoking and anxiety disorders during adolescence and early adulthood. JAMA. 2000;284:2348–51.
CAS
PubMed
Google Scholar
Jamal M, Does AJ, Penninx BW, Cuijpers P. Age at smoking onset and the onset of depression and anxiety disorders. Nicotine Tob Res. 2011;13:809–19.
PubMed
Google Scholar
Lai S, Lai H, Page JB, McCoy CB. The association between cigarette smoking and drug abuse in the United States. J Addict Dis. 2000;19:11–24.
CAS
PubMed
Google Scholar
Chen X, Unger JB, Palmer P, Weiner MD, Johnson CA, Wong MM, et al. Prior cigarette smoking initiation predicting current alcohol use evidence for a gateway drug effect among California adolescents from eleven ethnic groups. Addict Behav. 2002;27:799–817.
PubMed
Google Scholar
Hanna EZ, Grant BF. Parallels to early onset alcohol use in the relationship of early onset smoking with drug use and DSM‐IV drug and depressive disorders: findings from the national longitudinal epidemiologic survey. Alcohol Clin Exp Res. 1999;23:513–22.
CAS
PubMed
Google Scholar
Collaborators G 2019 MD. Global, regional, and national burden of 12 mental disorders in 204 countries and territories, 1990–2019: a systematic analysis for the Global Burden of Disease Study 2019. Lancet Psychiatry. 2022;9:137–50.
Google Scholar
Vigo D, Thornicroft G, Atun R. Estimating the true global burden of mental illness. Lancet Psychiatry. 2016;3:171–8.
PubMed
Google Scholar
Sowell ER, Thompson PM, Holmes CJ, Jernigan TL, Toga AW. In vivo evidence for post-adolescent brain maturation in frontal and striatal regions. Nat Neurosci. 1999;2:859–61.
CAS
PubMed
Google Scholar
Sowell ER, Peterson BS, Thompson PM, Welcome SE, Henkenius AL, Toga AW. Mapping cortical change across the human life span. Nat Neurosci. 2003;6:309–15.
CAS
PubMed
Google Scholar
Giedd JN, Blumenthal J, Jeffries NO, Castellanos FX, Liu H, Zijdenbos A, et al. Brain development during childhood and adolescence: a longitudinal MRI study. Nat Neurosci. 1999;2:861–3.
CAS
PubMed
Google Scholar
Gogtay N, Giedd JN, Lusk L, Hayashi KM, Greenstein D, Vaituzis AC, et al. Dynamic mapping of human cortical development during childhood through early adulthood. Proc Natl Acad Sci USA. 2004;101:8174–9.
CAS
PubMed
PubMed Central
Google Scholar
Petanjek Z, Judaš M, Šimic G, Rasin MR, Uylings HBM, Rakic P, et al. Extraordinary neoteny of synaptic spines in the human prefrontal cortex. Proc Natl Acad Sci USA. 2011;108:13281–6.
CAS
PubMed
PubMed Central
Google Scholar
Catts VS, Fung SJ, Long LE, Joshi D, Vercammen A, Allen KM, et al. Rethinking schizophrenia in the context of normal neurodevelopment. Front Cell Neurosci. 2013;7:60.
PubMed
PubMed Central
Google Scholar
Fung SJ, Webster MJ, Sivagnanasundaram S, Duncan C, Elashoff M, Weickert CS. Expression of interneuron markers in the dorsolateral prefrontal cortex of the developing human and in schizophrenia. Am J Psychiatry. 2010;167:1479–88.
PubMed
Google Scholar
Lewis DA. Development of the prefrontal cortex during adolescence: insights into vulnerable neural circuits in schizophrenia. Neuropsychopharmacology. 1997;16:385–98.
CAS
PubMed
Google Scholar
Parr AC, Calabro F, Larsen B, Tervo-Clemmens B, Elliot S, Foran W, et al. Dopamine-related striatal neurophysiology is associated with specialization of frontostriatal reward circuitry through adolescence. Prog Neurobiol. 2021;201:101997.
CAS
PubMed
PubMed Central
Google Scholar
Galvan A, Hare TA, Parra CE, Penn J, Voss H, Glover G, et al. Earlier development of the accumbens relative to orbitofrontal cortex might underlie risk-taking behavior in adolescents. J Neurosci. 2006;26:6885–92.
CAS
PubMed
PubMed Central
Google Scholar
Larsen B, Luna B. In vivo evidence of neurophysiological maturation of the human adolescent striatum. Dev Cogn Neurosci. 2014;12C:74–85.
Google Scholar
Larsen B, Olafsson V, Calabro F, Laymon C, Tervo-Clemmens B, Campbell E, et al. Maturation of the human striatal dopamine system revealed by PET and quantitative MRI. Nat Commun. 2020;11:846.
CAS
PubMed
PubMed Central
Google Scholar
Wahlstrom D, White T, Luciana M. Neurobehavioral evidence for changes in dopamine system activity during adolescence. Neurosci Biobehav Rev. 2010;34:631–48.
CAS
PubMed
Google Scholar
Luciana M, Wahlstrom D, Porter JN, Collins PF. Dopaminergic modulation of incentive motivation in adolescence: age-related changes in signaling, individual differences, and implications for the development of self-regulation. Dev Psychol. 2012;48:844–61.
PubMed
PubMed Central
Google Scholar
Tervo-Clemmens B, Calabro FJ, Parr AC, Fedor J, Foran W, Luna B. A canonical trajectory of executive function maturation from adolescence to adulthood. Nat Commun. 2023;14:6922.
CAS
PubMed
PubMed Central
Google Scholar
Somerville LH, Hare T, Casey BJ. Frontostriatal maturation predicts cognitive control failure to appetitive cues in adolescents. J Cogn Neurosci. 2011;23:2123–34.
PubMed
Google Scholar
Liston C, Watts R, Tottenham N, Davidson MC, Niogi S, Ulug AM, et al. Frontostriatal microstructure modulates efficient recruitment of cognitive control. Cereb Cortex. 2006;16:553–60.
PubMed
Google Scholar
Sawyer SM, Azzopardi PS, Wickremarathne D, Patton GC. The age of adolescence. Lancet Child Adolesc Health. 2018;2:223–8.
PubMed
Google Scholar
Schneider M. Adolescence as a vulnerable period to alter rodent behavior. Cell Tissue Res. 2013;354:99–106.
CAS
PubMed
Google Scholar
Granata L, Gildawie KR, Ismail N, Brenhouse HC, Kopec AM. Immune signaling as a node of interaction between systems that sex-specifically develop during puberty and adolescence. Dev Cogn Neurosci. 2022;57:101143.
CAS
PubMed
PubMed Central
Google Scholar
Spear LP. The adolescent brain and age-related behavioral manifestations. Neurosci Biobehav Rev. 2000;24:417–63.
CAS
PubMed
Google Scholar
Reynolds LM, Flores C. Mesocorticolimbic dopamine pathways across adolescence: diversity in development. Front Neural Circuit. 2021;15:735625.
CAS
Google Scholar
Hoops D, Kyne R, Salameh S, MacGowan D, Avramescu RG, Ewing E, et al. The scheduling of adolescence with netrin-1 and UNC5C. eLife. 2024;12:RP88261.
PubMed
PubMed Central
Google Scholar
Hollenstein T, Lougheed JP. Beyond storm and stress. Am Psychol. 2013;68:444–54.
PubMed
Google Scholar
Miller DJ, Duka T, Stimpson CD, Schapiro SJ, Baze WB, McArthur MJ, et al. Prolonged myelination in human neocortical evolution. Proc Natl Acad Sci USA. 2012;109:16480–5.
CAS
PubMed
PubMed Central
Google Scholar
Blakemore S-J. Imaging brain development: the adolescent brain. Neuroimage. 2012;61:397–406.
PubMed
Google Scholar
Yuan M, Cross SJ, Loughlin SE, Leslie FM. Nicotine and the adolescent brain. J Physiol. 2015;593:3397–412.
CAS
PubMed
PubMed Central
Google Scholar
Laviola G, Macrı̀ S, Morley-Fletcher S, Adriani W. Risk-taking behavior in adolescent mice: psychobiological determinants and early epigenetic influence. Neurosci Biobehav Rev. 2003;27:19–31.
PubMed
Google Scholar
Burke AR, Miczek KA. Stress in adolescence and drugs of abuse in rodent models: role of dopamine, CRF, and HPA axis. Psychopharmacology. 2013;231:1557–80.
PubMed
PubMed Central
Google Scholar
Yetnikoff L, Reichard RA, Schwartz ZM, Parsely KP, Zahm DS. Protracted maturation of forebrain afferent connections of the ventral tegmental area in the rat. J Comp Neurol. 2014;522:1031–47.
CAS
PubMed
PubMed Central
Google Scholar
Yetnikoff L, Pokinko M, Arvanitogiannis A, Flores C. Adolescence: a time of transition for the phenotype of dcc heterozygous mice. Psychopharmacology. 2014;231:1705–14.
CAS
PubMed
Google Scholar
Reynolds LM, Yetnikoff L, Pokinko M, Wodzinski M, Epelbaum JG, Lambert LC, et al. Early adolescence is a critical period for the maturation of inhibitory behavior. Cereb Cortex. 2019;29:3676–86.
PubMed
Google Scholar
Yetnikoff L, Almey A, Arvanitogiannis A, Flores C. Abolition of the behavioral phenotype of adult netrin-1 receptor deficient mice by exposure to amphetamine during the juvenile period. Psychopharmacology. 2011;217:505–14.
CAS
PubMed
Google Scholar
Reynolds LM, Hernandez G, MacGowan D, Popescu C, Nouel D, Cuesta S, et al. Amphetamine disrupts dopamine axon growth in adolescence by a sex-specific mechanism in mice. Nat Commun. 2023;14:4035.
CAS
PubMed
PubMed Central
Google Scholar
Changeux J-P. Nicotine addiction and nicotinic receptors: lessons from genetically modified mice. Nat Rev Neurosci. 2010;11:389–401.
CAS
PubMed
Google Scholar
Dwyer JB, McQuown SC, Leslie FM. The dynamic effects of nicotine on the developing brain. Pharmacol Ther. 2009;122:125–39.
CAS
PubMed
PubMed Central
Google Scholar
Dwyer JB, Broide RS, Leslie FM. Nicotine and brain development. Birth Defects Res C Embryo Today. 2008;84:30–44.
CAS
PubMed
Google Scholar
Doura MB, Gold AB, Keller AB, Perry DC. Adult and periadolescent rats differ in expression of nicotinic cholinergic receptor subtypes and in the response of these subtypes to chronic nicotine exposure. Brain Res. 2008;1215:40–52.
CAS
PubMed
PubMed Central
Google Scholar
Trauth JA, Seidler FJ, McCook EC, Slotkin TA. Adolescent nicotine exposure causes persistent upregulation of nicotinic cholinergic receptors in rat brain regions. Brain Res. 1999;851:9–19.
CAS
PubMed
Google Scholar
Counotte DS, Goriounova NA, Moretti M, Smoluch MT, Irth H, Clementi F, et al. Adolescent nicotine exposure transiently increases high‐affinity nicotinic receptors and modulates inhibitory synaptic transmission in rat medial prefrontal cortex. FASEB J. 2012;26:1810–20.
CAS
PubMed
Google Scholar
Cano M, Reynaga DD, Belluzzi JD, Loughlin SE, Leslie F. Chronic exposure to cigarette smoke extract upregulates nicotinic receptor binding in adult and adolescent rats. Neuropharmacology. 2020;181:108308.
CAS
PubMed
PubMed Central
Google Scholar
Levin ED, Lawrence SS, Petro A, Horton K, Rezvani AH, Seidler FJ, et al. Adolescent vs. adult-onset nicotine self-administration in male rats: duration of effect and differential nicotinic receptor correlates. Neurotoxicol Teratol. 2007;29:458–65.
CAS
PubMed
PubMed Central
Google Scholar
Renda A, Penty N, Komal P, Nashmi R. Vulnerability to nicotine self-administration in adolescent mice correlates with age-specific expression of α4* nicotinic receptors. Neuropharmacology. 2016;108:49–59.
CAS
PubMed
Google Scholar
Kota D, Martin BR, Robinson SE, Damaj MI. Nicotine dependence and reward differ between adolescent and adult male mice. J Pharmacol Exp Ther. 2007;322:399–407.
CAS
PubMed
Google Scholar
Britton AF, Vann RE, Robinson SE. Perinatal nicotine exposure eliminates peak in nicotinic acetylcholine receptor response in adolescent rats. J Pharmacol Exp Ther. 2007;320:871–6.
CAS
PubMed
Google Scholar
Ribeiro-Carvalho A, Lima CS, Medeiros AH, Siqueira NR, Filgueiras CC, Manhães AC, et al. Combined exposure to nicotine and ethanol in adolescent mice: effects on the central cholinergic systems during short and long term withdrawal. Neuroscience. 2009;162:1174–86.
CAS
PubMed
Google Scholar
Omelchenko N, Sesack SR. Laterodorsal tegmental projections to identified cell populations in the rat ventral tegmental area. J Comp Neurol. 2005;483:217–35.
PubMed
Google Scholar
Dautan D, Souza AS, Huerta-Ocampo I, Valencia M, Assous M, Witten IB, et al. Segregated cholinergic transmission modulates dopamine neurons integrated in distinct functional circuits. Nat Neurosci. 2016;19:1025–33.
CAS
PubMed
PubMed Central
Google Scholar
Christensen MH, Kohlmeier KA. Age‐related changes in functional postsynaptic nicotinic acetylcholine receptor subunits in neurons of the laterodorsal tegmental nucleus, a nucleus important in drug addiction. Addict Biol. 2016;21:267–81.
CAS
PubMed
Google Scholar
Christensen MH, Ishibashi M, Nielsen ML, Leonard CS, Kohlmeier KA. Age-related changes in nicotine response of cholinergic and non-cholinergic laterodorsal tegmental neurons: Implications for the heightened adolescent susceptibility to nicotine addiction. Neuropharmacology. 2014;85:263–83.
CAS
PubMed
PubMed Central
Google Scholar
de Kloet SF, Mansvelder HD, De Vries TJ. Cholinergic modulation of dopamine pathways through nicotinic acetylcholine receptors. Biochem Pharmacol. 2015;97:425–38.
PubMed
Google Scholar
Mansvelder HD, Rover MD, McGehee DS, Brussaard AB. Cholinergic modulation of dopaminergic reward areas: upstream and downstream targets of nicotine addiction. Eur J Pharmacol. 2003;480:117–23.
CAS
PubMed
Google Scholar
Naudé J, Dongelmans M, Faure P. Nicotinic alteration of decision-making. Neuropharmacology. 2015;96:244–54.
PubMed
Google Scholar
Naudé J, Tolu S, Dongelmans M, Torquet N, Valverde S, Rodriguez G, et al. Nicotinic receptors in the ventral tegmental area promote uncertainty-seeking. Nat Neurosci. 2016;19:471–8.
PubMed
Google Scholar
Maskos U, Molles BE, Pons S, Besson M, Guiard BP, Guilloux J-P, et al. Nicotine reinforcement and cognition restored by targeted expression of nicotinic receptors. Nature. 2005;436:103–7.
CAS
PubMed
Google Scholar
Faure P, Tolu S, Valverde S, Naudé J. Role of nicotinic acetylcholine receptors in regulating dopamine neuron activity. Neuroscience. 2014;282:86–100.
CAS
PubMed
Google Scholar
Fernandez SP, Broussot L, Marti F, Contesse T, Mouska X, Soiza-Reilly M, et al. Mesopontine cholinergic inputs to midbrain dopamine neurons drive stress-induced depressive-like behaviors. Nat Commun. 2018;9:4449.
PubMed
PubMed Central
Google Scholar
Cragg SJ. Meaningful silences: how dopamine listens to the ACh pause. Trends Neurosci. 2006;29:125–31.
CAS
PubMed
Google Scholar
Dautan D, Huerta-Ocampo I, Witten IB, Deisseroth K, Bolam JP, Gerdjikov T, et al. A major external source of cholinergic innervation of the striatum and nucleus accumbens originates in the brainstem. J Neurosci. 2014;34:4509–18.
PubMed
PubMed Central
Google Scholar
Islam KUS, Blaess S. The impact of the mesoprefrontal dopaminergic system on the maturation of interneurons in the murine prefrontal cortex. Front Neurosci. 2024;18:1403402.
PubMed
PubMed Central
Google Scholar
Reynolds LM, Flores C. Adolescent dopamine development: connecting experience with vulnerability or resilience to psychiatric disease. In: Martin CR, Preedy VR, Rajendram R, editors. Diagnosis, management and modeling of neurodevelopmental disorders. Academic Press; 2021. p. 295–304; https://doi.org/10.1016/B978-0-12-817988-8.00026-9.
Hoops D, Flores C. Making dopamine connections in adolescence. Trends Neurosci. 2017;40:709–19.
CAS
PubMed
PubMed Central
Google Scholar
O’Donnell P. Adolescent maturation of cortical dopamine. Neurotox Res. 2010;18:306–12.
PubMed
Google Scholar
Peters KZ, Naneix F. The role of dopamine and endocannabinoid systems in prefrontal cortex development: adolescence as a critical period. Front Neural Circuits. 2022;16:939235.
CAS
PubMed
PubMed Central
Google Scholar
McCutcheon JE, Conrad KL, Carr SB, Ford KA, McGehee DS, Marinelli M. Dopamine neurons in the ventral tegmental area fire faster in adolescent rats than in adults. J Neurophysiol. 2012;108:1620–30.
CAS
PubMed
PubMed Central
Google Scholar
Reynolds LM, Pokinko M, Torres-Berrío A, Cuesta S, Lambert LC, Pellitero EDC, et al. DCC receptors drive prefrontal cortex maturation by determining dopamine axon targeting in adolescence. Biol Psychiatry. 2018;83:181–92.
CAS
PubMed
Google Scholar
Vassilev P, Pantoja-Urban AH, Giroux M, Nouel D, Hernandez G, Orsini T, et al. Unique effects of social defeat stress in adolescent male mice on the Netrin-1/DCC pathway, prefrontal cortex dopamine and cognition (Social stress in adolescent vs. adult male mice). eNeuro. 2021;8:ENEURO.0045-21.2021.
PubMed
PubMed Central
Google Scholar
Corongiu S, Dessì C, Cadoni C. Adolescence versus adulthood: differences in basal mesolimbic and nigrostriatal dopamine transmission and response to drugs of abuse. Addict Biol. 2019. https://doi.org/10.1111/adb.12721.
Eddins D, Petro A, Levin ED. Impact of acute nicotine exposure on monoaminergic systems in adolescent and adult male and female rats. Neurotoxicol Teratol. 2022;93:107122.
CAS
PubMed
Google Scholar
Placzek AN, Zhang TA, Dani JA. Age dependent nicotinic influences over dopamine neuron synaptic plasticity. Biochem Pharmacol. 2009;78:686–92.
CAS
PubMed
PubMed Central
Google Scholar
Azam L, Chen Y, Leslie FM. Developmental regulation of nicotinic acetylcholine receptors within midbrain dopamine neurons. Neuroscience. 2007;144:1347–60.
CAS
PubMed
Google Scholar
Castro EM, Lotfipour S, Leslie FM. Nicotine on the developing brain. Pharmacol Res. 2023;190:106716.
CAS
PubMed
PubMed Central
Google Scholar
Leslie FM. Unique, long-term effects of nicotine on adolescent brain. Pharmacol Biochem Behav. 2020;197:173010.
CAS
PubMed
PubMed Central
Google Scholar
Linker KE, Elabd MG, Tawadrous P, Cano M, Green KN, Wood MA, et al. Microglial activation increases cocaine self-administration following adolescent nicotine exposure. Nat Commun. 2020;11:306.
CAS
PubMed
PubMed Central
Google Scholar
Ren M, Lotfipour S. Nicotine gateway effects on adolescent substance use. West J Emerg Med. 2019;20:696–709.
PubMed
PubMed Central
Google Scholar
Reed SC, Izenwasser S. Nicotine produces long-term increases in cocaine reinforcement in adolescent but not adult rats. Brain Res. 2017;1654:165–70.
CAS
PubMed
Google Scholar
Laviolette SR. Exploring the impact of adolescent exposure to cannabinoids and nicotine on psychiatric risk: insights from translational animal models. Psychol Med. 2019:1–8. https://doi.org/10.1017/S0033291719003325.
Laviolette SR. Molecular and neuronal mechanisms underlying the effects of adolescent nicotine exposure on anxiety and mood disorders. Neuropharmacology. 2020;184:108411.
PubMed
Google Scholar
Jobson CLM, Renard J, Szkudlarek H, Rosen LG, Pereira B, Wright DJ, et al. Adolescent nicotine exposure induces dysregulation of mesocorticolimbic activity states and depressive and anxiety-like prefrontal cortical molecular phenotypes persisting into adulthood. Cereb Cortex. 2018;29:3140–53.
Google Scholar
Hudson R, Green M, Wright DJ, Renard J, Jobson CEL, Jung T, et al. Adolescent nicotine induces depressive and anxiogenic effects through ERK 1‐2 and Akt‐GSK‐3 pathways and neuronal dysregulation in the nucleus accumbens. Addict Biol. 2020;26:e12891.
PubMed
Google Scholar
Ng THJ, Sarikahya MH, Hudson R, Szkudlarek HJ, Pérez-Valenzuela E, Uzuneser TC, et al. Adolescent nicotine exposure induces long-term, sex-specific disturbances in mood and anxiety-related behavioral, neuronal and molecular phenotypes in the mesocorticolimbic system. Neuropsychopharmacology. 2024;49:1171–82.
CAS
PubMed
PubMed Central
Google Scholar
Iñiguez SD, Warren BL, Parise EM, Alcantara LF, Schuh B, Maffeo ML, et al. Nicotine exposure during adolescence induces a depression-like state in adulthood. Neuropsychopharmacology. 2009;34:1609–24.
PubMed
Google Scholar
Picciotto MR, Higley MJ, Mineur YS. Acetylcholine as a neuromodulator: cholinergic signaling shapes nervous system function and behavior. Neuron. 2012;76:116–29.
CAS
PubMed
PubMed Central
Google Scholar
Lewis AS, Picciotto MR. High-affinity nicotinic acetylcholine receptor expression and trafficking abnormalities in psychiatric illness. Psychopharmacology. 2013;229:477–85.
CAS
PubMed
PubMed Central
Google Scholar
Higley MJ, Picciotto MR. Neuromodulation by acetylcholine: examples from schizophrenia and depression. Curr Opin Neurobiol. 2014;29:88–95.
CAS
PubMed
Google Scholar
Terry AV, Jones K, Bertrand D. Nicotinic acetylcholine receptors in neurological and psychiatric diseases. Pharmacol Res. 2023;191:106764.
CAS
PubMed
Google Scholar
Saricicek A, Esterlis I, Maloney KH, Mineur YS, Ruf BM, Muralidharan A, et al. Persistent β2*-nicotinic acetylcholinergic receptor dysfunction in major depressive disorder. Am J Psychiatry. 2012;169:851–9.
PubMed
PubMed Central
Google Scholar
Martin-Ruiz CM, Haroutunian VH, Long P, Young AH, Davis KL, Perry EK, et al. Dementia rating and nicotinic receptor expression in the prefrontal cortex in schizophrenia. Biol Psychiatry. 2003;54:1222–33.
CAS
PubMed
Google Scholar
Marutle A, Zhang X, Court J, Piggott M, Johnson M, Perry R, et al. Laminar distribution of nicotinic receptor subtypes in cortical regions in schizophrenia. J Chem Neuroanat. 2001;22:115–26.
CAS
PubMed
Google Scholar
Koukouli F, Rooy M, Tziotis D, Sailor KA, O’Neill HC, Levenga J, et al. Nicotine reverses hypofrontality in animal models of addiction and schizophrenia. Nat Med. 2017;23:347–54.
CAS
PubMed
PubMed Central
Google Scholar
Morel C, Fernandez SP, Pantouli F, Meye FJ, Marti F, Tolu S, et al. Nicotinic receptors mediate stress-nicotine detrimental interplay via dopamine cells’ activity. Mol Psychiatry. 2017;36:1418.
Google Scholar
Ortiz V, Campos RC, Fofo H, Fernandez SP, Barik J. Nicotinic receptors promote susceptibility to social stress in female mice linked with neuroadaptations within VTA dopamine neurons. Neuropsychopharmacology. 2022;47:1587–96.
CAS
PubMed
PubMed Central
Google Scholar
Mineur YS, Soares AR, Etherington IM, Abdulla ZI, Picciotto MR. Pathophysiology of nAChRs: Limbic circuits and related disorders. Pharmacol Res. 2023;191:106745.
CAS
PubMed
Google Scholar
Ananth MR, Rajebhosale P, Kim R, Talmage DA, Role LW. Basal forebrain cholinergic signalling: development, connectivity and roles in cognition. Nat Rev Neurosci. 2023;24:233–51.
CAS
PubMed
PubMed Central
Google Scholar
Role LW, Berg DK. Nicotinic receptors in the development and modulation of CNS synapses. Neuron. 1996;16:1077–85.
CAS
PubMed
Google Scholar
Ren M, Lotfipour S, Leslie F. Unique effects of nicotine across the lifespan. Pharmacol Biochem Behav. 2022;214:173343.
CAS
PubMed
PubMed Central
Google Scholar
Goriounova NA, Mansvelder HD. Nicotine exposure during adolescence alters the rules for prefrontal cortical synaptic plasticity during adulthood. Front Synaptic Neurosci. 2012;4:3.
CAS
PubMed
PubMed Central
Google Scholar
Abreu-Villaça Y, Seidler FJ, Qiao D, Tate CA, Cousins MM, Thillai I, et al. Short-term adolescent nicotine exposure has immediate and persistent effects on cholinergic systems: critical periods, patterns of exposure, dose thresholds. Neuropsychopharmacology. 2003;28:1935–49.
PubMed
Google Scholar
Slotkin TA, Cousins MM, Seidler FJ. Administration of nicotine to adolescent rats evokes regionally selective upregulation of CNS α7 nicotinic acetylcholine receptors. Brain Res. 2004;1030:159–63.
CAS
PubMed
Google Scholar
Adriani W, Spijker S, Deroche-Gamonet V, Laviola G, Moal ML, Smit AB, et al. Evidence for enhanced neurobehavioral vulnerability to nicotine during periadolescence in rats. J Neurosci. 2003;23:4712–6.
CAS
PubMed
PubMed Central
Google Scholar
Kota D, Robinson SE, Damaj MI. Enhanced nicotine reward in adulthood after exposure to nicotine during early adolescence in mice. Biochem Pharmacol. 2009;78:873–9.
CAS
PubMed
Google Scholar
Slotkin TA, Ryde IT, MacKillop EA, Bodwell BE, Seidler FJ. Adolescent nicotine administration changes the responses to nicotine given subsequently in adulthood: Adenylyl cyclase cell signaling in brain regions during nicotine administration and withdrawal, and lasting effects. Brain Res Bull. 2008;76:522–30.
CAS
PubMed
Google Scholar
Trauth JA, McCook EC, Seidler FJ, Slotkin TA. Modeling adolescent nicotine exposure: effects on cholinergic systems in rat brain regions. Brain Res. 2000;873:18–25.
CAS
PubMed
Google Scholar
Wise RA. Dopamine, learning and motivation. Nat Rev Neurosci. 2004;5:483–94.
CAS
PubMed
Google Scholar
Schultz W. Behavioral dopamine signals. Trends Neurosci. 2007;30:203–10.
CAS
PubMed
Google Scholar
Bromberg-Martin ES, Matsumoto M, Hikosaka O. Dopamine in motivational control: rewarding, aversive, and alerting. Neuron. 2010;68:815–34.
CAS
PubMed
PubMed Central
Google Scholar
Orsini CA, Moorman DE, Young JW, Setlow B, Floresco SB. Neural mechanisms regulating different forms of risk-related decision-making: insights from animal models. Neurosci Biobehav Rev. 2015;58:147–67.
PubMed
PubMed Central
Google Scholar
Coddington LT, Dudman JT. Learning from action: reconsidering movement signaling in midbrain dopamine neuron activity. Neuron. 2019;104:63–77.
CAS
PubMed
Google Scholar
Cools R, D’Esposito M. Inverted-U-shaped dopamine actions on human working memory and cognitive control. Biol Psychiatry. 2011;69:e113–25.
CAS
PubMed
PubMed Central
Google Scholar
Berke JD. What does dopamine mean? Nat Neurosci. 2018;21:1–793.
Google Scholar
Volkow ND, Wise RA, Baler R. The dopamine motive system: implications for drug and food addiction. Nat Rev Neurosci. 2017;18:741–52.
CAS
PubMed
Google Scholar
Toda M, Abi-Dargham A. Dopamine hypothesis of schizophrenia: making sense of it all. Curr Psychiatry Rep. 2007;9:329–36.
PubMed
Google Scholar
Dunlop BW, Nemeroff CB. The role of dopamine in the pathophysiology of depression. Arch Gen Psychiatry. 2007;64:327–37.
CAS
PubMed
Google Scholar
Schulz J, Zimmermann J, Sorg C, Menegaux A, Brandl F. Magnetic resonance imaging of the dopamine system in schizophrenia – a scoping review. Front Psychiatry. 2022;13:925476.
PubMed
PubMed Central
Google Scholar
Gurvich C, Rossell SL. Dopamine and cognitive control: sex-by-genotype interactions influence the capacity to switch attention. Behav Brain Res. 2015;281:96–101.
CAS
PubMed
Google Scholar
Papaleo F, Erickson L, Liu G, Chen J, Weinberger DR. Effects of sex and COMT genotype on environmentally modulated cognitive control in mice. Proc Natl Acad Sci USA. 2012;109:20160–5.
CAS
PubMed
PubMed Central
Google Scholar
Haddon JE, Killcross S. Rat prefrontal dopamine and cognitive control: impaired and enhanced conflict performance. Behav Neurosci. 2011;125:344–9.
PubMed
Google Scholar
Baarendse PJJ, Counotte DS, O’Donnell P, Vanderschuren LJMJ. Early social experience is critical for the development of cognitive control and dopamine modulation of prefrontal cortex function. Neuropsychopharmacology. 2013;38:1485–94.
CAS
PubMed
PubMed Central
Google Scholar
Barth B, Portella AK, Dubé L, Meaney MJ, Silveira PP. The interplay between dopamine and environment as the biological basis for the early origins of mental health. In: Early Life Origins of Ageing and Longevity. Springer; 2019. p. 121–40. https://doi.org/10.1007/978-3-030-24958-8_7.
Nguyen C, Mondoloni S, Borgne TL, Centeno I, Come M, Jehl J, et al. Nicotine inhibits the VTA-to-amygdala dopamine pathway to promote anxiety. Neuron. 2021. https://doi.org/10.1016/j.neuron.2021.06.013.
Eddine R, Valverde S, Tolu S, Dautan D, Hay A, Morel C, et al. A concurrent excitation and inhibition of dopaminergic subpopulations in response to nicotine. Sci Rep. 2015;5:8184.
CAS
PubMed
PubMed Central
Google Scholar
Exley R, Maubourguet N, David V, Eddine R, Evrard A, Pons S, et al. Distinct contributions of nicotinic acetylcholine receptor subunit α4 and subunit α6 to the reinforcing effects of nicotine. Proc Natl Acad Sci USA. 2011;108:7577–82.
CAS
PubMed
PubMed Central
Google Scholar
Tolu S, Eddine R, Marti F, David V, Graupner M, Pons S, et al. Co-activation of VTA DA and GABA neurons mediates nicotine reinforcement. Mol Psychiatry. 2013;18:382–93.
CAS
PubMed
Google Scholar
Cadoni C, Felice MD, Corongiu S, Dessì C, Espa E, Melis M, et al. Role of genetic background in the effects of adolescent nicotine exposure on mesolimbic dopamine transmission. Addict Biol. 2019;25:e12803.
PubMed
Google Scholar
Vrettou M, Thalhammer SB, Svensson A-L, Dumas S, Nilsson KW, Wallén-Mackenzie Å, et al. Vesicular glutamate transporter 2 expression in the ventral tegmental area of outbred male rats following exposure to nicotine and alcohol. Drug Alcohol Depend Rep. 2023;8:100180.
PubMed
PubMed Central
Google Scholar
Thomas AM, Ostroumov A, Kimmey BA, Taormina MB, Holden WM, Kim K, et al. Adolescent nicotine exposure alters GABAA receptor signaling in the ventral tegmental area and increases adult ethanol self-administration. Cell Rep. 2018;23:68–77.
CAS
PubMed
PubMed Central
Google Scholar
Smith RF, McDonald CG, Bergstrom HC, Ehlinger DG, Brielmaier JM. Adolescent nicotine induces persisting changes in development of neural connectivity. Neurosci Biobehav Rev. 2015;55:432–43.
CAS
PubMed
Google Scholar
Manitt C, Eng C, Pokinko M, Ryan RT, Torres-Berrío A, Lopez JP, et al. dcc orchestrates the development of the prefrontal cortex during adolescence and is altered in psychiatric patients. Transl Psychiatry. 2013;3:e338.
CAS
PubMed
PubMed Central
Google Scholar
Counotte DS, Spijker S, Van de Burgwal LH, Hogenboom F, Schoffelmeer AN, De Vries TJ, et al. Long-lasting cognitive deficits resulting from adolescent nicotine exposure in rats. Neuropsychopharmacology. 2009;34:299–306.
CAS
PubMed
Google Scholar
Goriounova NA, Mansvelder HD. Nicotine exposure during adolescence leads to short- and long-term changes in spike timing-dependent plasticity in rat prefrontal cortex. J Neurosci. 2012;32:10484–93.
CAS
PubMed
PubMed Central
Google Scholar
Counotte DS, Goriounova NA, Li KW, Loos M, van der Schors RC, Schetters D, et al. Lasting synaptic changes underlie attention deficits caused by nicotine exposure during adolescence. Nat Neurosci. 2011;14:417–9.
CAS
PubMed
Google Scholar
Trauth JA, Seidler FJ, Ali SF, Slotkin TA. Adolescent nicotine exposure produces immediate and long-term changes in CNS noradrenergic and dopaminergic function. Brain Res. 2001;892:269–80.
CAS
PubMed
Google Scholar
Reynolds LM, Gulmez A, Fayad SL, Campos RC, Rigoni D, Nguyen C, et al. Transient nicotine exposure in early adolescent male mice freezes their dopamine circuits in an immature state. Nat Commun. 2024;15:9017.
CAS
PubMed
PubMed Central
Google Scholar
Nolley EP, Kelley BM. Adolescent reward system perseveration due to nicotine: studies with methylphenidate. Neurotoxicol Teratol. 2007;29:47–56.
CAS
PubMed
Google Scholar
Matta SG, Balfour DJ, Benowitz NL, Boyd RT, Buccafusco JJ, Caggiula AR, et al. Guidelines on nicotine dose selection for in vivo research. Psychopharmacology. 2007;190:269–319.
CAS
PubMed
Google Scholar
Allain F, Minogianis E-A, Roberts DCS, Samaha A-N. How fast and how often: the pharmacokinetics of drug use are decisive in addiction. Neurosci Biobehav Rev. 2015;56:166–79.
PubMed
Google Scholar
Alam F, Silveyra P. Sex differences in E-cigarette use and related health effects. Int J Environ Res Public Health. 2023;20:7079.
PubMed
PubMed Central
Google Scholar
Yimsaard P, McNeill A, Yong H-H, Cummings KM, Chung-Hall J, Hawkins SS, et al. Gender differences in reasons for using electronic cigarettes and product characteristics: findings from the 2018 ITC four country smoking and vaping survey. Nicotine Tob Res. 2020;23:678–86.
PubMed Central
Google Scholar
Wong DN, Fan W. Ethnic and sex differences in E-cigarette use and relation to alcohol use in California adolescents: the California Health Interview Survey. Public Health. 2018;157:147–52.
CAS
PubMed
Google Scholar
Moen JK, Lee AM. Sex differences in the nicotinic acetylcholine receptor system of rodents: impacts on nicotine and alcohol reward behaviors. Front Neurosci. 2021;15:745783.
PubMed
PubMed Central
Google Scholar
Picciotto MR. Nicotine as a modulator of behavior: beyond the inverted U. Trends Pharmacol Sci. 2003;24:493–9.
CAS
PubMed
Google Scholar
Jung Y, Hsieh LS, Lee AM, Zhou Z, Coman D, Heath CJ, et al. An epigenetic mechanism mediates developmental nicotine effects on neuronal structure and behavior. Nat Neurosci. 2016;19:905–14.
CAS
PubMed
PubMed Central
Google Scholar
Miller AD, Blaha CD. Midbrain muscarinic receptor mechanisms underlying regulation of mesoaccumbens and nigrostriatal dopaminergic transmission in the rat. Eur J Neurosci. 2005;21:1837–46.
PubMed
Google Scholar
Forster GL, Blaha CD. Laterodorsal tegmental stimulation elicits dopamine efflux in the rat nucleus accumbens by activation of acetylcholine and glutamate receptors in the ventral tegmental area. Eur J Neurosci. 2000;12:3596–604.
CAS
PubMed
Google Scholar
Yeomans J, Forster G, Blaha C. M5 muscarinic receptors are needed for slow activation of dopamine neurons and for rewarding brain stimulation. Life Sci. 2001;68:2449–56.
CAS
PubMed
Google Scholar
Glantz S, Jeffers A, Winickoff JP. Nicotine addiction and intensity of e-cigarette use by adolescents in the US, 2014 to 2021. JAMA Netw Open. 2022;5:e2240671.
PubMed
PubMed Central
Google Scholar
Volesky KD, Maki A, Scherf C, Watson LM, Cassol E, Villeneuve PJ. Characteristics of e-cigarette users and their perceptions of the benefits, harms and risks of e-cigarette use: survey results from a convenience sample in Ottawa, Canada. Heal Promot Chronic Dis Prev Can. 2016;36:130–8.
CAS
Google Scholar
Coleman BN, Johnson SE, Tessman GK, Tworek C, Alexander J, Dickinson DM, et al. “It’s not smoke. It’s not tar. It’s not 4000 chemicals. Case closed”: exploring attitudes, beliefs, and perceived social norms of e-cigarette use among adult users. Drug Alcohol Depend. 2016;159:80–85.
PubMed
Google Scholar
Leventhal AM, Stone MD, Andrabi N, Barrington-Trimis J, Strong DR, Sussman S, et al. Association of e-cigarette vaping and progression to heavier patterns of cigarette smoking. JAMA. 2016;316:1918.
PubMed
PubMed Central
Google Scholar
Kinnunen JM, Ollila H, Minkkinen J, Lindfors PL, Timberlake DS, Rimpelä AH. Nicotine matters in predicting subsequent smoking after e-cigarette experimentation: a longitudinal study among finnish adolescents. Drug Alcohol Depend. 2019;201:182–7.
CAS
PubMed
Google Scholar
Martinelli T, Candel MJJM, de Vries H, Talhout R, Knapen V, van Schayck CP, et al. Exploring the gateway hypothesis of e-cigarettes and tobacco: a prospective replication study among adolescents in the Netherlands and Flanders. Tob Control. 2023;32:170–8.
PubMed
Google Scholar
Goldenson NI, Leventhal AM, Stone MD, McConnell RS, Barrington-Trimis JL. Associations of electronic cigarette nicotine concentration with subsequent cigarette smoking and vaping levels in adolescents. JAMA Pediatr. 2017;171:1192.
PubMed
PubMed Central
Google Scholar





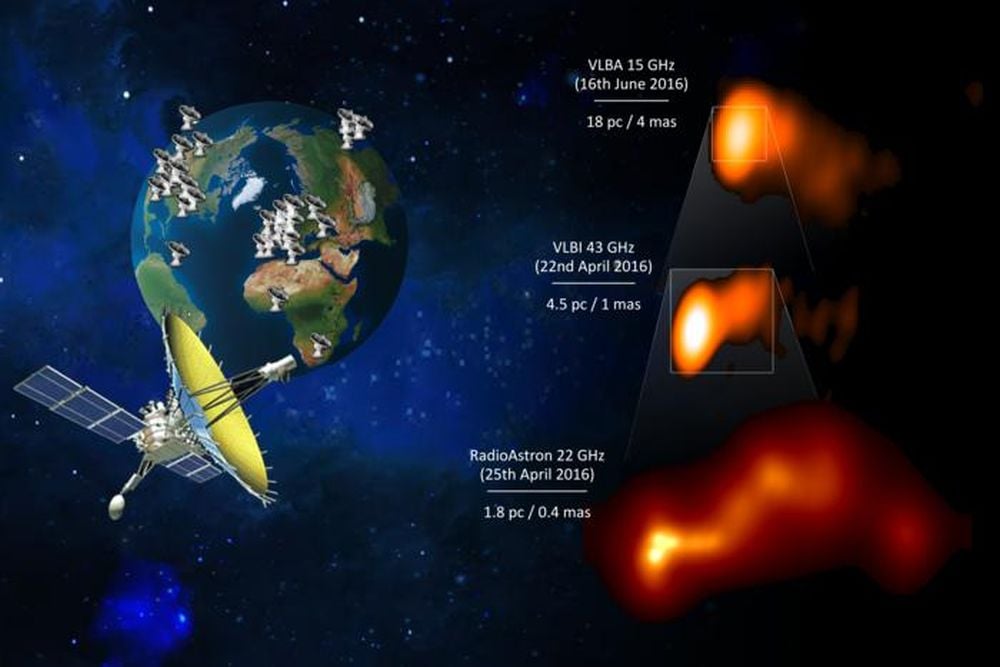
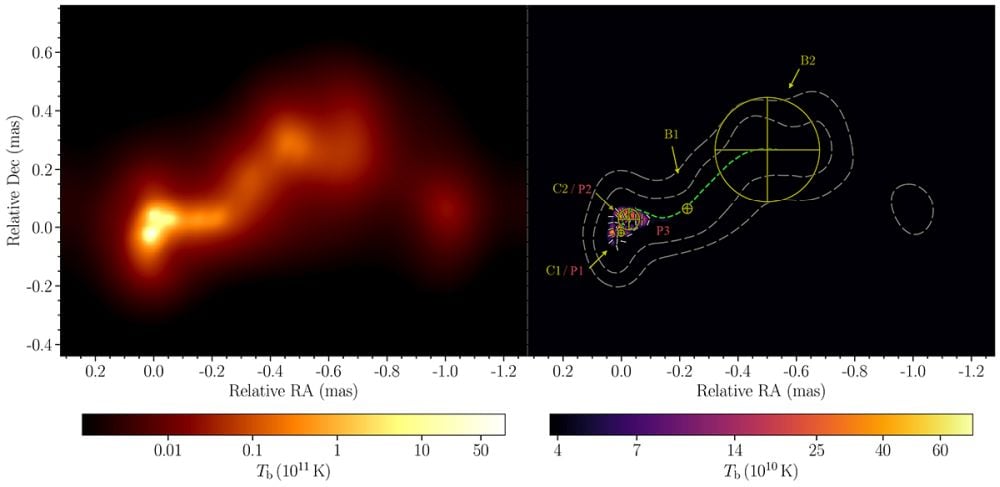 These images of OJ 287 are from April 25, 2016. The image on the left shows brightness temperature. The image on the right shows total intensity contours. P1, P2, and P3 are polarized features, and the central dashed green curve traces the jet ridgeline. Yellow circles C1 and C2 mark the locations of the black holes. Image Credit: Traianou et al. 2025. A&A
These images of OJ 287 are from April 25, 2016. The image on the left shows brightness temperature. The image on the right shows total intensity contours. P1, P2, and P3 are polarized features, and the central dashed green curve traces the jet ridgeline. Yellow circles C1 and C2 mark the locations of the black holes. Image Credit: Traianou et al. 2025. A&A
