Overview of software, data and workflow
We conducted our LSP mapping workflow using Google Earth Engine (GEE) (v.0.1.404 or later)65 and performed additional analyses using Python66 with a set of core scientific packages (numpy67, shapely68, pandas69, geopandas70, rasterio71, xarray72, rasterstats73, dask74, scipy75, scikit-learn76, statsmodels77 and matplotlib78). All of the datasets used in our study are summarized in Supplementary Table 1, and our entire mapping workflow is summarized in Extended Data Fig. 1a.
LSP datasets
We used GEE to model LSP in two independent time series of remote sensing indices that are strong correlates of seasonal variability in plant productivity—NIRV, an index of the fraction of incident near-infrared light that is reflected by vegetation20, and SIF, an index of the quantity of incident photons that are absorbed by chlorophyll and re-emitted as fluorescence21. We used a 20-year time series of MODIS-derived NIRV data (daily data from 2001 to 2020, subsampled to every 4 days for computational tractability) as our main dataset (the full workflow diagram is shown in Extended Data Fig. 1a). Following best practices for estimation of patterns at the annual timescale, we chose the MCD43A4 v061 dataset34, a 16-day temporal composite79 of nadir bidirectional reflectance distribution function (BRDF)-adjusted reflectance80. We used the version of these data that is publicly available in the GEE data catalogue. We did not carry out topographic correction because the scale of our analysis (0.05°; ~5.5 km) is sufficiently coarse that spatial averaging is expected to remove topographic bias80,81. We used only pixels with quality values of ≤3 (that is, pixels for which full or magnitude-based BRDF inversions were successfully fitted82) for both the red and NIR bands (bands 1 and 2), aggregated to our target analytical resolution of 0.05° (hereafter, target resolution) using the arithmetic mean. We calculated NIRV, as described previously20, as the product of the NDVI and total NIR reflectance. NIRV values of ≤0, assumed to be invalid20, occurred predominantly in high-albedo scenes (for example, treeless snow cover; Extended Data Fig. 2d), where productivity is assumed to be minimal, so they were clamped to the minimum positive NIRV value observed during a pixel’s 20-year time series.
To evaluate our NIRV maps, we ran some of our main analyses identically but using a global, gridded SIF dataset35. This is a roughly 4.3-year (September 2014 to January 2019), 0.05°, spatially contiguous time series dataset, interpolated by artificial neural network (ANN) from the spatially discontiguous SIF data measured along Orbiting Carbon Observatory 2 (OCO-2) orbital swaths. Rigorous internal and external validation of this dataset showed that it accurately captured the global patterns present in the original OCO-2 retrievals and that it explained 81% of the variation in contemporaneous chlorophyll fluorescence imaging spectrometer aerial measurements taken beneath OCO-2 orbits and 72% of the variation in measurements not beneath orbits35. We downloaded this dataset from the Distributed Active Archive Center for Biogeochemical Dynamics83 then ingested it into GEE.
Given that the SIF dataset interpolates across orbital gaps but the paper describing the dataset did not explicitly validate the seasonal phenological patterns of the interpolated data, we assessed the observed seasonality in the interpolated, orbital-gap data against the observed seasonality in another, coarser-resolution SIF dataset collected by the TROPOspheric Monitoring Instrument (TROPOMI)84,85. To do so, we extracted SIF time series from the ANN-interpolated dataset at a sample of random points drawn within OCO-2 orbital gaps in three tropical realms (the Neotropics, tropical Africa, and Indo-Pacific and tropical Australia; Extended Data Fig. 6c) then compared those values to contemporaneous time series extracted from the TROPOMI SIF data. We used tropical regions for this assessment because their lack of a pronounced thermal winter creates the greatest possibility that seasonality there exhibits spatially varying patterns that are not accurately recovered by spatial interpolation from orbital-swath data. If the interpolated dataset adequately captures the true seasonal patterns of SIF within OCO-2 orbital gaps then its time series should explain the bulk of the variation in the TROPOMI time series, and it does (R2 = 0.89; Extended Data Fig. 6c).
Data filtering
To exclude locations where our harmonic regression-based LSP mapping methodology (see the next section) would return inaccurate results, we used an extensive filtering pipeline that removed invalid land cover, pixels with multiple types of data deficiency and pixels with statistically insignificant LSP regressions. The pixels removed from analysis by each of the filtering steps described below are mapped and summarized in Extended Data Fig. 1b.
For land-cover filtering, we used the GEE data catalog asset for MCD12C1.06186, a MODIS product estimating annual, global land cover at our target resolution. We used the Annual International Geosphere-Biosphere Programme’s (IGBP) classification scheme (land cover type 1). To avoid low-quality data originating from non-target land cover, we excluded data from all pixels with >10% invalid land cover—including urban and built-up land, permanent snow and ice, barren land and water bodies (categories 13, 15, 16 and 0)—for all years within which that classification was assigned. Next, we retained pixels with any other land-cover classifications provided that they never switched between agricultural (categories 12 or 14) and non-agricultural (categories 1 to 11), to avoid fitting phenocycles to the noise resulting from abrupt changes between natural phenologies and those that are deliberately altered by human management (for example, irrigation). We retained pixels where land-cover assignment changed across the time series but was either always agricultural or always non-agricultural because: (1) spurious signals of change between natural land-cover types are common in regions with large, climatically driven interannual variation in plant productivity or where the actual land cover straddles categorical boundaries and challenges classification algorithms (for example, woodland, savanna and semi-arid biomes); (2) actual land-use and land-cover change (LULCC) on the ground is often too subtle to register a change in remotely sensed land-cover maps (for example, selective logging), even when it registers a clear signal in continuous metrics such as NIRV (Extended Data Fig. 2a); and (3) we only expected other forms of LULCC (for example, deforestation) to affect our modelling results in regions where different land-cover types exhibit different natural phenologies in response to the same broad bioclimatic controls, in which case pixels subject to LULCC should generate model fits that are intermediate to the phenocycles typical of the before and after land-cover types, introducing some noise into our map but neither preventing interpretation of its overarching patterns nor invalidating significant statistical results.
While the LSP of agricultural regions is of interest in many contexts, anthropogenic LSP patterns caused by irrigation and other intensive land management practices3 could confound our phenological asynchrony analyses, which focus on the climatic drivers and evolutionary implications of longstanding, naturally occurring LSP gradients. Because of this, we used a stricter masking procedure for all datasets used to calculate LSP asynchrony maps and to run asynchrony-related analyses, omitting data from all agricultural pixels (IGBP categories 12 and 14; Extended Data Fig. 1b).
To preclude poorly fitted LSP regressions that could cause spurious results, we removed any target-resolution pixels with data that did not satisfy a set of strict non-missingness criteria. First, we removed any pixels whose LSP time series had >50% missing data, a simple step to remove sites with data dropout because of substantial cloud contamination or MODIS quality control problems. Next, we removed any pixels without at least 10% monthly mean data availability in every month of the year. Finally, owing to a tendency for the harmonic regression procedure (described below) to interpolate spurious second LSP peaks into extended, seasonally repeating periods of missing data (for example, during high-latitude winters, when Terra and Aqua overpasses occur outside daylight hours for numerous weeks), we removed any pixels for which the binary time series of data availability (0 = missing data, 1 = data available) had a Pielou’s evenness87 of less than 0.8. We calculated Pielou’s evenness, J′ = H′/H′max, using H′ (Shannon’s diversity index88) calculated with 12 values, each value being a monthly average proportion of non-missing 4-day-interval data over the 20-year NIRV time series. Manual inspection of fitted phenological patterns after applying this series of filtering steps confirmed successful removal of locations that would otherwise produce spurious results. These last two steps removed all locations north of roughly 60° (Extended Data Fig. 1b) because the lack of winter daylight during satellite overpass creates long, seasonally repeating stretches of unavailable data. This is also a known complication for other remote-sensing products (for example, MOD44B.061 Vegetation Continuous Fields89), but it does not affect our major findings because the same orbital physics that causes this issue also produces strong, zonally consistent temperature and photoperiod control over annual phenologies at these latitudes and, therefore, limited potential for phenological asynchrony.
Finally, we used the harmonic regression procedure described below not only to calculate characteristic annual LSP patterns but also to estimate the significance of those patterns and filter out pixels with insignificant regression results, using a Monte Carlo framework. To do this, for each pixel in our global NIRV dataset, we randomly permuted the original LSP time-series image stack, scrambling any true seasonal signal, then ran the harmonic regression and stored an image of the R2 values at all pixels. Next, we calculated from all of the stored R2 images a single summary image of empirical P values indicating, for each pixel, the proportion of permutations for which the permuted time series’ R2 values exceeded the R2 value from the unpermuted harmonic regression. We ran this harmonic regression permutation test using 20 permutations at every pixel globally (because of computational limitations), then filtered out any pixels with an empirical P ≥ 0.05.
Modelling of LSP
We used harmonic regression to model the long-term average annual LSP pattern (that is, phenocycle) of every pixel in the global, filtered NIRV and SIF datasets. In our model each pixel’s full time series is predicted as a function of time as:
$$y={beta }_{0}+{beta }_{t}t+{beta }_{1}sin ({t}_{{rm{ann}}})+{beta }_{2}cos ({t}_{{rm{ann}}})+{beta }_{3}sin ({t}_{{rm{sem}}})+{beta }_{4}cos ({t}_{{rm{sem}}})+{epsilon },$$
where y is either the SIF or NIRV time series, t is the linear time component (days from the start of the time series), and tann and tsem are circular time expressed in annual (ann) and semiannual (sem) frequencies (that is, the day of year expressed in radians, where 2π radians corresponds to the last day of the year for tann and to the middle and last days of the year for tsem). We then retained all of the resulting coefficient maps except βt (the trend), yielding a stack of five coefficient maps that represents the detrended, long-term, characteristic annual LSP pattern at each pixel globally.
We chose harmonic regression because it is a simple, widely used and clearly interpretable approach to time-series analysis90, and because it would enable us to characterize the long-term average annual behaviour at all terrestrial locations. Our regression formulation is algebraically equivalent to detrending the full 20-year time series, then running a Fourier transform that includes both annual and semiannual frequency components91. We designed a number of the data-filtering approaches described above to ensure against the spurious interpolation into seasonally repeating data gaps that could otherwise be caused by this method. We chose to include both the annual and semiannual frequencies in the harmonic regression to strike a balance between model complexity and overfitting. We expected that complex annual LSP patterns would occur in locations that have bimodal seasonal precipitation patterns (that is, two rainy seasons)50 and no winter freeze47. Indeed, preliminary analysis revealed numerous regions with stronger bimodal than unimodal annual LSP patterns (that is, regions containing many pixels whose R2 values were higher in semiannual-only harmonic regression models than in annual-only models). The linear combination of annual and semiannual harmonic regression components is complex enough to represent annual LSP curves that are unimodal, evenly bimodal (two equal peaks and troughs) or unevenly bimodal (featuring major and minor peaks and troughs), but not more complex, and therefore avoids overfitting by excluding unfounded higher frequencies90.
While frequency-specific phase and amplitude estimates could be recovered from the fitted coefficients of our models, their comparative interpretation across such a wide range of phenological patterns would be difficult. Thus, for all downstream analysis and visualization, we instead use Euclidean distances and multivariate statistics calculated directly on the fitted phenocycles, which can be calculated as the multiplication of a pixel’s fitted harmonic regression coefficients with the 1-year matrix of daily time values expressed in linear time and in annual and semi-annual cyclical time. Extended Data Fig. 2a–d pairs multivariate visualization (methods described below) with demonstrations of the phenocycle-fitting procedure in various test regions, and Extended Data Fig. 2e shows a similar visualization screenshotted from the GEE app that we created for public exploration of our results (the link to which is provided within the GitHub repository for this project; https://github.com/erthward/phen_asynch, https://doi.org/10.5281/zenodo.15671259)92.
Evaluation of LSP mapping
We first evaluated the annual NIRV LSP map by calculating and inspecting a map of R2 values between the fitted NIRV and SIF phenocycles at all pixels (Extended Data Fig. 6b). We also checked the distribution of unimodal and bimodal phenologies against prior studies. To do this, we min–max scaled each pixel’s phenocycle to the [0, 1] interval and rotated it to start at its minimum value (to avoid problems arising from phenocycle peaks that straddle the start of the calendar year). We then extracted the heights of each phenocycle’s peaks, using the ‘find_peaks’ function in the ‘signal’ module of the Python package scipy (v.1.13.0)75, and used the absolute difference of those heights as an indicator of where a pixel lies on a spectrum between perfectly bimodal (0: indicating two peaks of equal height) and unimodal (1: assigned to phenologies having only a single peak). We mapped this index (Extended Data Fig. 6a), then visually compared it to previously published depictions of the global distribution of regions with one versus two growing seasons (see figure 3 of ref. 4).
We also evaluated the fitted phenocycles for both LSP datasets (NIRV, SIF) by comparison with average phenocycles fitted identically to time series of PhenoCam36 NDVI and FLUXNET201537,50 GPP. For the PhenoCam analysis, we used a combination of the R93 package phenocamapi (v.0.1.5)94 and custom Python code to download all available (as of 5 March 2025) 3-day summary NDVI datasets from all cameras and regions of interest (ROIs; masked areas of uniform vegetation within a camera’s field of view, which are used to generate separate time series datasets). We used NDVI because its phenological signal, which can diverge from that of the green chromatic coordinate in some systems36, provides a better comparator to our NDVI-derived NIRV data. We used the 3-day summaries because they have reduced noise, and we analysed the 75th-percentile NDVI summary values to strike a reasonable trade-off between the tendency of higher-percentile values to be less noisy under variable lighting conditions and the risk that very high percentiles can cause outlier influence95. We dropped any camera sites that PhenoCam reports as belonging to any of the invalid IGBP land cover classes that we filtered out of our LSP analysis (urban and built-up land, permanent snow and ice, barren land and water bodies) or as being agricultural (because agricultural management could cause an entirely different phenology within a camera’s field of view than the spatially averaged phenological signal reflected in our LSP map), leaving a total of 368 camera sites eligible for analysis. Before fitting a harmonic regression for each site, we removed outliers from each of the site’s ROI datasets (using the outlier flag provided by PhenoCam), then combined all datasets by averaging each day’s values across all ROIs to approximate the integrated land cover signal in our LSP dataset at that site. We then used the same harmonic regression model used in the LSP-fitting procedure described above to calculate a set of five coefficients describing the detrended, average annual NDVI phenology for a site, and from those coefficients performed matrix multiplication to recover the fitted characteristic annual NDVI phenocycle for each site. Finally, for each site, we calculated the R2 values between the site’s characteristic annual NDVI phenocycle and the LSP phenocycle corresponding to the site (that is, the pixel where the camera is located or, if that pixel is masked in our LSP dataset, the nearest valid pixel within a two-pixel-wide box that surrounds it). We summarized this evaluation procedure across all camera sites by producing, for each LSP dataset: (1) a scatter plot of the LSP-NDVI R2 values plotted on the Whittaker biomes96, to depict bioclimatic patterns in evaluation performance; and (2) a scatterplot comparing LSP-NDVI R2 values to NDVI time series lengths, to depict the relationship between camera data availability and evaluation performance (Extended Data Fig. 6d).
For the FLUXNET2015 comparison, we manually downloaded all datasets available at the time of access (11 October 2021), then, as with PhenoCam, dropped all flux tower sites reporting invalid and agricultural land cover types, yielding 170 valid GPP datasets for analysis. Before fitting a harmonic regression to each dataset, we first removed all datapoints with a daily quality value of <0.7 (that is, with <70% measured or good-quality gap-filled data contributing to their daily aggregated values). We then used the same methods as described for the PhenoCam NDVI comparison above to fit a harmonic regression, predict a characteristic annual time series, calculate R2 values between the annual time series and those from their closest available LSP pixels (up to 2 pixels distant, otherwise a tower’s dataset was dropped) and visualize the results (Extended Data Fig. 6e).
LSP visualization
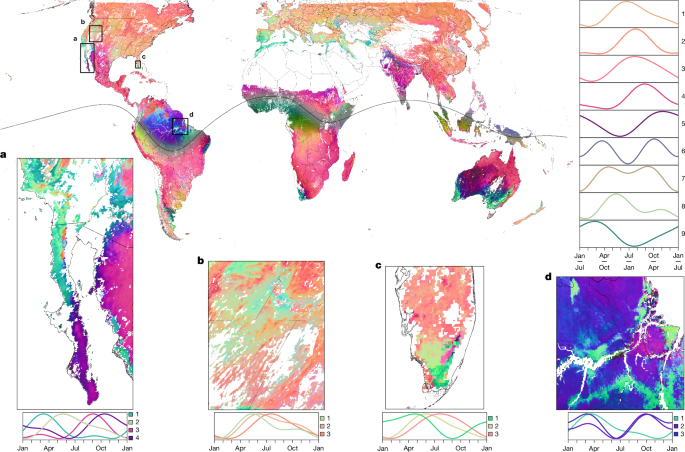
To visualize the global variability of seasonal LSP that is present in the results of our harmonic regression, we used colour-composite visualization of the results of a dimensionality-reduction analysis to produce a single global map. First, we used Python v.3.7 and the eofs package (v.1.4.0)97 to run EOF analysis on the covariance matrix of the global set of NIRV phenocycles. We standardized each pixel’s phenocycle before EOF calculation, ensuring that all pixels had equal variances of 1 and therefore allowing the EOF analysis to highlight global variability in the shape and timing of LSP patterns, our topic of interest, irrespective of spatial variation in NIRV amplitude. Following common practice in EOF analysis, we used the square root of the cosine of the latitude as pixel area weights.
This calculation reduced the global diversity of average annual LSP patterns to four EOFs. Finding that the first three EOFs cumulatively explain >90% of the variation in the dataset (91.62%; Extended Data Fig. 4a), we min–max scaled them, then displayed them using the RGB colour channels, visualizing the bulk majority of global LSP variability within a single map. As they have embedded within them both the unremarkable north–south hemispheric seasonality dipole and hemisphere-independent patterns of interest (for example, monsoon-driven LSP dynamics), we transformed the raw EOF maps before RGB visualization to represent phenological variability in a globally consistent colour scheme. To accomplish this, we used WebPlotDigitizer98 to digitize a geospatial vector file of the mean ITCZ in both boreal summer (June, July, August) and boreal winter (December, January, February)38, then calculated a single, annual mean ITCZ vector by averaging the boreal summer and winter latitudes at evenly spaced longitudes around the globe. Finally, for each EOF, we constructed a synthetic, transformed map by calculating w × EOF + (1 − w) × (1 − EOF), where w varies from 1 in the northern hemisphere to 0 in the southern hemisphere and transitions linearly from 1 to 0 within a 10° latitudinal band surrounding the annual mean ITCZ. We chose to use the ITCZ as the latitudinal boundary across which to transform the EOF maps because it serves as a more natural meteorological Equator than does the geographical Equator17,38. To help to interpret the result of this visualization across the region surrounding the ITCZ (Fig. 1), where some colour-warping occurs, we also generated RGB composite maps using untransformed EOF maps and using EOF maps transformed uniformly as 1 − EOF (Extended Data Fig. 4b,c). As this transformation is used only for visual comparison across hemispheres, it has no influence on any of the analytical results reported in our work.
To depict the characteristic phenocycles corresponding to the RGB visualization, we use mini-batch k-means clustering (a version of the standard k-means clustering algorithm that reduces computational burden by using only a fixed-size random subsample of the full dataset at each iteration) to cluster the standardized, fitted phenocycles within a region into k colours, for k = 1:12, then visually inspect a scree plot to determine the optimal value of k. Using that chosen value, we assign each pixel to one of k clusters, then plot each cluster centre (after min–max scaling) as its characteristic phenocycle, coloured by the median RGB value across all pixels in the cluster. We used this procedure to produce plots interpreting the predominant phenocycles both globally (Fig. 1 (main)) and within various focal regions (Fig. 1a–d and Extended Data Fig. 5). Before clustering the global map, we rotated the fitted phenocycles of all pixels below the mean ITCZ by 182 days (that is, half a year) to allow similar phenologies in the northern and southern hemispheres to cluster together.
Discovering regional phenological variability in the Great Basin of the United States that appeared to match the cheatgrass-invaded, sagebrush and montane phenologies presented previously42, we used ancillary data from ref. 43, aggregated to the target resolution of our map, to calculate the average estimated percentage of annual herbaceous cover in each of the three predominant clusters depicted in our analysis (Fig. 1b). To support our interpretation of the three clusters as annual-invaded communities, sagebrush and montane vegetation, which we based on the differences in their estimated average annual herbaceous cover and on a visual comparison to ref. 42, we used ANOVA to test for a significance difference in the estimated percentage of annual herbaceous cover across all three clusters, followed by a Tukey’s honest significant difference test to test for significant pairwise differences between the clusters.
To better highlight complex geographical patterns of spatially variable LSP timing, we also produced a video (Supplementary Video 1) animating the min–max scaled average NIRV phenocycle at each pixel. Scaling each pixel’s phenocycle in this way forces all pixels to a common annual amplitude (from zero to one), ignoring spatial differences in intra-annual variability caused by variable ecosystem productivity, and thus highlighting spatial differences in the timing and rates of change of LSP.
Calculation of phenological asynchrony
We exported the GEE results of our filtered harmonic regression as a global set of tiled, multiband images of regression coefficients. We used GEE’s TensorFlow output format and ‘kernelSize’ argument to generate tiles that overlapped their neighbours by 300 km (double the largest neighbourhood size in our asynchrony calculations), to allow asynchrony to be calculated independently and in parallel.
For each LSP dataset (NIRV, SIF), we calculated our asynchrony metric pixel-wise, for all pixels with at least 30 available neighbours, using an algorithm based on Martin et al.12 and depicted in Extended Data Fig. 7a:
-
(1)
Calculate the standardized phenocycle for a focal pixel.
-
(2)
Identify all pixels of which the centrepoints are within the chosen neighbourhood radius of the focal pixel (the neighbour pixels).
-
(3)
For each neighbour pixel: (a) calculate its standardized phenocycle; (b) calculate the 365-dimensional Euclidean phenological distance between its phenocycle and the focal pixel’s phenocycle; (c) calculate its geographical (geodesic) distance to the focal pixel.
-
(4)
Calculate asynchrony as the slope of the regression of Euclidean phenological neighbour distances on geographical neighbour distances (or as zero, wherever the slope has P > 0.01).
We used a regression approach to calculate the asynchrony metric because it explicitly estimates the spatial rate of change in phenology, and therefore well represents the spatial rate of change of seasonal timing that is the subject of the ASH12. We standardized phenocycles, nullifying differences in amplitude, before calculating Euclidean distances between them, therefore preserving the timing differences that we are interested in, even between similar-shape but out-of-phase curves (a criterion not met by other common distance metrics, such as dynamic time warping). We ran this calculation in Julia (v.1.4.1)99 on UC Berkeley’s Savio cluster, parallelized by tile, then mosaicked the results into a global map (Fig. 2a).
We produced this global map for each of three neighbourhood radii (50, 100, and 150 km), enabling us to check the sensitivity of our maps and our downstream results to this decision. The values of the resulting maps, expressed as a spatial rate of change in the target variable’s units (that is, Δunittarget_variable/Δm), scale arbitrarily with a map’s neighbourhood radius, but each map provides an internally valid quantitative basis for assessing and comparing asynchrony between sites. To assess the overall level of agreement between the NIRV and SIF asynchrony maps, despite the fine-scale noise expected in a neighbourhood metric, we mapped and scatter plotted pixel-wise comparisons between the two datasets for each of the three neighbourhood radii (Extended Data Fig. 8). Moreover, to evaluate the scale-sensitivity of the LSP asynchrony maps (and of the asynchrony maps that we likewise calculated for the climatic covariates described below), we assessed, for each mapped variable, the R2 values for all three pairwise interneighbourhood map comparisons (Extended Data Fig. 7b).
To visually depict the asynchrony algorithm, we first simulated harmonic-regression output for a low-asynchrony region as a five-layer stack of coefficient values with rasters of low relative-magnitude Gaussian noise added to them and for a high-asynchrony region as a five-layer stack of mean coefficient values with large relative-magnitude, spatially autocorrelated noise added to them using neutral landscape models generated using the nlmpy Python package100. We represented each five-layer simulated map as a single-layer map by first calculating each pixel’s phenocycle from its simulated vector of harmonic regression coefficients, then calculating the day of the year when its simulated phenocycle attains its peak value. We used this summary map, all pixels’ simulated phenocycles and the phenological-distance–geographical-distance regression (the slope of which serves as the asynchrony metric) to graphically depict the asynchrony calculation procedure (Extended Data Fig. 7a).
Phenological asynchrony model covariates
For the random-forest (RF) model exploring the potential drivers of phenological asynchrony (see below), we produced rasters of physiographic and environmental covariates using workflows combining GEE, Julia, Python and GDAL (v.2.2.3)101. First, we applied the same harmonic regression and asynchrony-mapping pipeline described above, skipping the masking steps that were specific to LSP data quality concerns, to the 64-year TerraClimate time series dataset102 in the GEE catalogue, generating asynchrony maps for the climatic factors potentially driving phenological asynchrony: monthly minimum and maximum temperature, monthly precipitation and monthly climate water deficit. We supplemented this with an equivalently produced map of asynchrony in cloud cover, using cloud cover fractions calculated from the internal cloud algorithm flag bit (bit 10 of the 1 km reflectance data QA band) of the MODIS Aqua and Terra daily 1 km global surface reflectance datasets (MYD09GA.061103 and MOD09GA.06104) in the GEE catalogue. The R2 values from these harmonic regressions are also mapped in Extended Data Fig. 3, and the asynchrony of the climatic factors is mapped in Extended Data Fig. 7.
To model the potential importance of topographic complexity for driving phenological asynchrony, we downloaded a global map of the vector ruggedness metric105. We chose this over other measures of topographic complexity because of its reduced correlation with slope. We downloaded data published previously106, choosing a map based on Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010) elevation data107 and median-aggregated at a scale on par with the neighbourhood size of our main LSP asynchrony dataset (100 km).
To allow the model to reflect phenological asynchrony between structurally distinct vegetation communities, we used GEE to create a global map of entropy in vegetation structure within 100 km neighbourhoods (hereafter, the vegetation entropy map). To do this, we used the same 20-year time series of annual MODIS IGBP 0.05° land cover86 that we used in our LSP data-filtering workflow. We reclassed land cover into categories of forest (IGBP classes 1–5: evergreen or deciduous broadleaf or needleleaf forests and mixed forest), shrubland (IGBP classes 6 and 7: closed and open shrublands), savanna (IGBP classes 8 and 9: woody savannas and savannas), grassland (IGBP class 10) or permanent wetland (IGBP class 11). We then applied the same mask used to calculate LSP asynchrony, so that the information captured by this covariate would reflect the information included in the LSP asynchrony response variable. Next, we reduced the 20-year time series to a single map representing the modal class for each pixel across all years. Finally, we produced the covariate map by calculating the entropy of the vegetation structure classes within each pixel’s 100 km radius (the neighbourhood size of our main analysis) as −Σi P(ci) log2P(ci), where c is vegetation structure class and P(ci) is the proportion of the neighbourhood that is assigned class i.
As LSP asynchrony patterns could be influenced by human LULCC, we used GEE to create two other 100-km neighbourhood covariates: the mean proportion of subpixels classified as LULCC, and the mean frequency of fire. We derived the mean LULCC proportion map from a global, harmonized map of Landsat-resolution (30 m) land-cover change and land use in 2019108. In GEE, we calculated the proportion of subpixels within each of our target-resolution pixels that were classified as any land-cover change or land-use class, including classes 92–116 and 212–236 (tree cover loss since 2000, with or without regrowth), classes 240–249 (built-up land) and class 252 (cropland). We applied to that LULCC proportion map the same mask used to calculate LSP asynchrony, then calculated the mean within a 100 km radial neighbourhood for every pixel.
As the source data for the LULCC map explicitly excludes fire-driven tree cover loss, we also used GEE to produce a separate covariate map estimating the neighbourhood mean frequency of fire. To do this, for each pixel we counted the number of months with a recorded burn date in the global monthly MODIS Burned Area dataset, MCD64A1.061109, divided that by the total number of months in the dataset, used the arithmetic mean to aggregate the map from its original 500 m resolution to our target resolution, applied the same mask applied to the map used to calculate LSP asynchrony, then calculated the mean of that fire frequency map within each pixel’s 100 km radial neighbourhood.
Modelling phenological asynchrony drivers
To explore the potential drivers of LSP asynchrony, we constructed an RF model using the R package ranger (v.0.13.1)110 and incorporating the set of covariates described above, formulated as:
$${{rm{LSP}}.{rm{asy}}}_{{rm{neigh}}} sim {{rm{ppt}}.{rm{asy}}}_{{rm{neigh}}}+{{rm{tmp}}.min .{rm{asy}}}_{{rm{neigh}}}+{{rm{tmp}}.max .{rm{asy}}}_{{rm{neigh}}}+{{rm{def}}.{rm{asy}}}_{{rm{neigh}}}+{{rm{cld}}.{rm{asy}}}_{{rm{neigh}}}+{rm{vrm}}.{rm{med}}+{rm{veg}}.{rm{ent}}+{rm{luc}}.{rm{prp}}.{rm{mea}}+{rm{brn}}.{rm{frq}}.{rm{mea}}[+x+y],$$
where LSP.asy is asynchrony of the LSP dataset used in a given model (either NIRV or SIF), ppt.asy is PA, tmp.min.asy and tmp.max.asy are minimum and maximum temperature asynchrony, def.asy is climate water deficit asynchrony, cld.asy is cloud cover asynchrony, neigh indicates the asynchrony neighbourhood radius used to calculate the asynchrony metrics for a given model (50, 100 or 150 km), veg.ent is vegetation structural entropy, vrm.med is the median vector ruggedness metric, luc.prp.mea is mean proportion of LULCC, brn.frq.mea is mean fire frequency, and x and y are pixel longitude and latitude (within brackets to indicate their inclusion in only half of the suite of models). We chose the RF algorithm owing to its ability to robustly model nonlinear relationships, suited to our expectation that phenological asynchrony would be driven by different and potentially interacting factors in different regions of the globe. We developed a comprehensive and conservative modelling workflow, which we ran once for each combination of LSP dataset (NIRV, SIF), neighbourhood radius (50 km, 100 km, 150 km), and coordinate inclusion (geographical coordinates either included or excluded as covariates). We examined the sensitivity of our RF models to the inclusion of geographical coordinates because of the lack of consensus about how to handle spatial data in RF modelling111,112. This produced a final set of 12 models (Extended Data Fig. 9a). As we found that salient results were largely insensitive to choice of LSP dataset, neighbourhood radius and coordinate inclusion, we chose the 100 km, NIRV-based, coordinates-included model as the main model to summarize and discuss in the main text of this article.
Before producing final results, we used R v.4.0.3 to prepare the modelling data, tune hyperparameters and carry out feature selection. First, we projected the response and covariate rasters to a metric projection (EPSG:3857) to ensure that coordinates were expressed in metres, then stacked them and extracted their values at all valid (that is, non-masked) pixels. Next, we carried out comprehensive hyperparameter tuning113, assessing model performance as a function of five RF tuning parameters (number of trees per forest: ‘ntree’ = 150, 200, 250, 300; fraction of observations to use in each tree, for tree decorrelation: ‘sample.fraction’ = 0.3, 0.55, 0.8; minimum number of observations that can be captured by a node: ‘min.node.size’ = 1, 3, 5, 10; size of random subset of variables from which to choose each node’s split variable: ‘mtry’ = 1, 3, 5; and whether to sample with replacement: ‘replace’ = true, false) and as a function of the fraction of the full global dataset used for modelling (‘subset.frac’ = 0.05, 0.005; drawn as a random subsample, quartile-stratified by the LSP response variable, to reduce the computational demand imposed by the size of the modelling dataset without causing excessive information loss). We included geographical coordinates in all models used for hyperparameter tuning, as we intended to retain them in the main model unless we found that predominant results were highly sensitive to their inclusion. We used as a performance metric the root mean squared error (r.m.s.e.) of the model fitted to a 60% training split of the subsampled global dataset and found that the r.m.s.e. of the predictions made on the 40% test split yielded the same set of optimum-performance hyperparameter choices. Lastly, before running the final set of models, we confirmed that none of our subsetted datasets contained variables with a collinearity of R2 ≥ 0.75, and we used the Boruta feature-selection algorithm and R package (Boruta v.7.0.0)114 to select our final feature set (but found no features that should be dropped).
We constructed the final 12 models using the optimum hyperparameters indicated by our tuning results (ntree = 300, sample.fraction = 0.8, min.node.size = 1, mtry = 5, replace = false and subset.frac = 0.05). To evaluate each model, we calculated two variable importance metrics—ranger’s default permutation-based importance metric, which compares the cross-tree average accuracy of out-of-bag sample predictions to the accuracy after permuting covariate values, and the absolute SHAP values115 summed across all predictions in a model’s training dataset, calculated using the R fastshap package (v.0.0.7)116—as well as two metrics of overall model performance, R2 and r.m.s.e. To help with spatial model assessment, we used trained models to make LSP asynchrony predictions at all global pixels, then calculated prediction error maps (Extended Data Fig. 9b shows the error map for the main model). Lastly, to aid spatial interpretability of the models, we calculated pixel-wise SHAP values and produced global SHAP maps for each covariate.
Noting low variability across models in the covariates identified as having the highest importance (Extended Data Fig. 9a), we summarized the main model (100-km NIRV asynchrony, coordinates included) in the text and estimated the predominance of the top two covariates in that model, PA (ppt.asy) and MTA (tmp.min.asy), as a normalized difference of absolute SHAP values: predom = (|SHAPppt.asy| − |SHAPtmp.min.asy|)/(|SHAPppt.asy| + |SHAPtmp.min.asy|). We plotted a summary map of the normalized difference across global regions of high LSP asynchrony (that is, pixels ≥85th percentile), to show regional variation in the predominance or codominance of these two drivers (Fig. 2b; Extended Data Fig. 9c shows predominance across all covariates except geographical coordinates).
Isoclimatic phenological asynchrony
To test the hypothesis that phenological asynchrony is less dependent on climatic difference at low latitudes than at higher latitudes, we performed an ensemble analysis. Each sub-analysis in the ensemble first uses clustering to delineate a global set of high-asynchrony regions, then uses matrix regressions to estimate the slope of the relationship between climatic and phenological distance (hereafter, the climate–phenology correlation) within each of those regions. We defined the sub-analyses within the ensemble using unique combinations of low, middle and high values for three hyperparameters to which our final results could exhibit sensitivity, then used Monte Carlo analysis to assess the relationship, across the ensemble, between regions’ mean latitudes and the strengths of their climate–phenology correlations.
To delineate high-asynchrony regions, we first converted our NIRV LSP asynchrony map into a map of maximum asynchrony pixels by setting all pixels ≥95th percentile asynchrony value to 1 and masking everything else. We then used the density-based spatial clustering of applications with noise (DBSCAN) algorithm117, implemented in the Python package sklearn (v.1.0.2)76, to cluster those high-asynchrony pixels. We chose the DBSCAN algorithm owing to its ability to robustly identify clusters of arbitrary shape around the high-density centres of a point set without forcing all points to have cluster assignments, which was a good match for the noisiness of our asynchrony map. Finally, we used the alpha-complex algorithm (a straight-line edge variant of the alpha-hull algorithm), implemented in Python by the Alpha Shape Toolbox (alphashape, v.1.3.1)118, to delineate high-asynchrony regions around those clusters. This enabled us to relax the convexity and contiguity assumptions of other hull-determination algorithms and, therefore, to flexibly delineate regions with complex shapes (for example, mountain arcs) without inevitably including all intervening geographical areas, as would occur with convex hulls.
To assess the relationship between the mean latitude of a region and the strength of the climate–phenology correlation within that region, we first standardized and stacked each of the 19 WorldClim bioclimatic variables119 and standardized our global map of fitted phenocycles. Then, for each delineated region, we executed the following steps:
-
(1)
Draw a set of 1,000 random points within the region that all fall within non-masked NIRv LSP pixels (or draw the maximum number of points possible, if regions are too small for 1,000 points).
-
(2)
Calculate the matrix of pairwise phenological distances (distphen) between all points (as 365-dimensional pairwise Euclidean distances between phenocycles).
-
(3)
Calculate the matrix of pairwise climatic distances (distclim) between all points (as 19-dimensional pairwise Euclidean distances between bioclimatic values).
-
(4)
Calculate the matrix of pairwise geographical distances (distgeog) between all points (as geodesic distances).
-
(5)
Standardize all three pairwise distance matrix variables (so that coefficients of all regressions are β coefficients and, therefore, comparable), then run MMRR53 using the formula phenology ~ βc climate + βg geography, where βc and βg indicate the strengths of the relationships between climatic and phenological distances and between geographical and phenological distances, respectively.
To hedge against hyperparameter sensitivity, we chose reasonable ranges of low, middle and high values of the key parameters in the clustering and hull-delineation algorithms from which to compose our ensemble. The DBSCAN clustering algorithm relies on two parameters to which our results might be sensitive: ‘eps’ (epsilon), the maximum geographical distance between two points that can be considered to be in the same neighbourhood; and ‘min_samples’, the minimum number of samples required within a neighbourhood for a point to be considered as a core point. The alpha-complex algorithm has an additional parameter to which our results might be sensitive: ‘alpha’, a value controlling how edge members are chosen and, therefore, determining the maximum complexity of a hull’s edge. To create the ensemble, we reran the full regionalization and climate–phenology correlation analysis once for each combination of the following parameter values: eps = 2, 3.5, 5; min_samples = 0.3, 0.45, 0.6; and alpha = 0.25, 0.75, 1.25.
As a final step, we summarized the ensemble results across the 27 parameterizations by running the ordinary least squares regression model ({beta }_{{rm{c}}} sim {gamma }_{{rm{lat}}}| overline{{rm{lat}}}| ), using γlat to quantify the relationship between the absolute value of the mean latitude of each cluster and the strength of its climate–phenology correlation (Fig. 3b). As this regression violates the assumption that samples of the independent variables are IID—each point represents a clustered and delineated high-asynchrony region, and those regions can overlap across distinct parameterizations of the sub-analyses—we used Monte Carlo analysis to generate an empirical P value for γlat in the ensemble linear regression model. We ran 1,000 iterations of the same regression, each time permuting the vector of (| overline{{rm{lat}}}| ) values, then calculated an empirical P value as the fraction of the 1,000 simulated γlat that are at least as extreme as the observed γlat (Fig. 3c). To provide a spatially explicit geographical interpretation of the results of this analysis, we mapped a summary of the ensemble results as a hexbin map (Fig. 3a), with the colour of each hexbin indicating the mean βc of all high-asynchrony regions (that is, delineated alpha hulls) overlapping the bin’s hexagon.
Allochrony by allopatry: flowering
To explore the ability of remotely sensed LSP to predict geographical variation in flowering phenology, we tested the correlation between NIRV phenocycles and dates of flowering observations for all available iNaturalist taxa with non-unimodal flowering histograms and without extremely broad latitudinal distributions. First, we used the Python API client pyinaturalist (v.0.19.0)120 to download from iNaturalist the weekly flowering-observation histogram, and the first ≤5,000 native, non-captive, research-grade flowering observations corresponding to that histogram, for every taxon having ≥50 annotated flowering observation records at the time of download (downloads completed between 5 June 2024, 23:00 UTC and 9 June 2024, 00:00 UTC). This included a total of 7,251 taxa out of the 34,438 iNaturalist taxa with at least one observation (21.1%). We truncated the raw observation datasets to ≤5,000 per taxon to limit strain on the iNaturalist API; preliminary results showed that this decision was inconsequential because none of the 39 taxa affected would ultimately be retained for later analyses.
We further filtered the observation points for each taxon to only those with at least 1 km positional accuracy, then used the alpha-complex algorithm118, with alpha set to 0.75 (the middle value used in our isoclimatic phenological asynchrony analysis) to fit a conservative geographical boundary (hereafter, observation range) to the set of iNaturalist observations. One taxon dropped out of our analysis at this stage because of the failure to fit an observation range. We then estimated the number of peaks in the flowering-week histogram for each taxon using the following steps:
-
(1)
‘Rotate’ the histogram so that the first instance of its minimum value moved into the first position in the vector, to avoid spurious results arising from flowering peaks that straddle the last and first weeks of the calendar year.
-
(2)
Fit a kernel density estimation (KDE) to the histogram, using a bandwidth of 5 weeks, to reduce the noise resulting from temporal variance in observation counts.
-
(3)
Use a simple, neighbour-comparison-based peak-search algorithm (implemented in the find_peaks function in the signal module of the Python package scipy v.1.13.0)75 to count the number of peaks in the KDE with a height ≥60% of the overall range of values in the histogram.
-
(4)
Calculate the absolute value of the lag-1 temporal autocorrelation in the observed KDE and in KDEs fitted to 100 permuted versions of the rotated flowering histogram.
-
(5)
If the non-permuted KDE has an empirical P ≤ 0.05 (that is, if the absolute value of the lag-1 temporal autocorrelation of the non-permuted KDE is greater than that of ≥95% of the permuted KDEs), then it has a significant signal of temporal autocorrelation that probably represents non-random seasonal variability in flowering activity, so assign the counted number of peaks as the observed number of flowering-time peaks for the taxon; otherwise, assign zero as the observed number of statistically significant flowering-time peaks.
Executing this procedure for all available taxa resulted in 6391 taxa (88.2%) with unimodal flowering-time histograms and 859 non-unimodal taxa, including 123 taxa (1.7%) with bimodal histograms, one taxon with a trimodal histogram and 735 taxa (10.1%) with no statistically significant flowering-time peaks. We dropped the unimodal taxa from further analysis because they were unlikely to exhibit the sharp geographical discontinuities in flowering phenology that were our main interest. We retained the 859 non-unimodal taxa to test for significant signals of allochrony by allopatry. We summarized these results by creating a set of hexbins covering all fitted observation ranges and then mapping, for each hexagon, the proportions of taxa with zero and with ≥2 flowering-time peaks and the overall proportion of all non-unimodal taxa (Extended Data Fig. 10). To preclude significant but uninteresting results for taxa broadly distributed across latitudes, and therefore affected by the opposite seasonalities of the northern and southern hemispheres, we dropped any taxa with samples extending beyond both 10° north and south latitudes (196 taxa).
We then looked for evidence of allochrony by allopatry by testing each of the 663 remaining taxa for a correlation between intersite flowering-date distances and intersite LSP distances. To do this, we fitted an MMRR model for each taxon, specified as flowering_date ~ βLSP LSP + βC climate + βG geography, where the variables are pairwise distance matrices and βLSP and its P value were our output values of interest, indicating the strength and statistical significance of the relationship between LSP and flowering date distances after accounting for environmental and geographical distances. Some non-unimodal taxa may flower opportunistically, perennially or at multiple discrete times of year within the same sites, and should therefore yield insignificant βLSP values, but taxa exhibiting the strong geographical discontinuities in flowering time that we would expect under allochrony by allopatry should yield a significant, positive βLSP value. To produce the distance covariates for this model, we calculated flowering date distances as the shorter of the two forward-time or backward-time distances between two observations’ numerical day-of-year values, LSP distances as the 365-dimensional Euclidean distances between the observation sites’ NIRV phenocycles, climate distances as the 19-dimensional Euclidean distances between the sites’ vectors of standardized WorldClim119 bioclimatic variables and geographical distances as the geodesic distances between sites. We corrected βLSP P values to control for the false-discovery rate (FDR) using the ‘false_discovery_control’ function in the ‘stats’ module of the Python package scipy (v.1.13.0)75 with the Benjamini–Hochberg method. Supplementary Table 4 provides results for the 43 taxa that remained significant after FDR control (of 614 taxa successfully tested, after 49 dropped out because of insufficient data for model-fitting), and the full results from all stages of this analysis are archived with the data for this study.
To visualize the results of this analysis for an example taxon, we plotted a temporal comparison between the flowering observation dates and the flowering observation locations’ min-max scaled phenocycles as well as a map of the observation locations, coloured according to k-means clustering of the phenocycles (k = 2) to highlight the spatial and temporal structure of the geographical discontinuity in phenology. We constructed this visualization (Fig. 4a) for two example taxa with FDR-corrected significance, chosen to demonstrate the correspondence of their patterns of allochrony by allopatry to the regional LSP patterns we had mapped and highlighted earlier in the article (M. scabra, in southwestern North America; S. parviflorum, in South Africa).
Allochrony by allopatry: genetics
To test whether remotely sensed LSP predicts the phenologically driven isolation by time22 that is expected to result from allochrony by allopatry, above and beyond isolation by distance121 and isolation by environment122, we fitted genetic MMRR models to a pair of datasets from two of the few published genetic studies of the ASH, substituting LSP distances calculated from our dataset for the authors’ previously used measures of asynchronous seasonality, then compared our results to theirs. First, we gathered and prepared the genomic and geographical data from the only genomic test of the ASH of which we are aware, a study of the eastern Brazilian toad R. granulosa25. We used the R package adegenet (v.2.1.5)123,124 and data downloaded from the Dryad repository for that study (https://datadryad.org/stash/dataset/doi:10.5061/dryad.pc866t1p4) to calculate a pairwise genetic distance matrix for 80 samples collected from 51 localities, based on the Euclidean distance between allele frequencies at 7,674 independent single-nucleotide polymorphism loci. We calculated geographical- and LSP-distance matrices as described above, using the geographical coordinates of each sample, and prepared a climatic distance matrix using the Euclidean distances between standardized versions of the four WorldClim119 bioclimatic variables used in the original study: annual mean temperature (BIO1), temperature seasonality (BIO4), annual precipitation (BIO12) and precipitation seasonality (BIO15). Five samples fell within masked pixels in our LSP dataset and thus could not be included in our analysis, yielding a final sample size of 75. We fit an MMRR model specified as genetic ~ βLSP LSP + βC climate + βG geography, then compared our results to the results presented in table 4 of ref. 25. To visualize our findings we used k-means clustering with Euclidean distances to divide the samples into k = 2 clusters, first clustering by NIRV phenocycles, then a second time clustering by genetic distance vectors. We then prepared side-by-side equivalent plots showing sample localities and their min–max-scaled phenocycles, coloured by either of those clusterings, providing a simple visual indication of the extent to which our LSP map recapitulates the observed genetic structure (Fig. 4b (top)).
To explore whether disparately related, sympatric taxa might exhibit similar patterns of isolation by asynchrony, we repeated the same procedure for the only other sympatric genetic dataset that we could find within previous studies of the ASH: cytochrome B sequencing data for the lesser woodcreeper (X. fuscus; Furnariidae)32. We first downloaded sample location data from the Zenodo archive for the study (http://zenodo.org/records/5012226)125 and the FASTA-formatted sample sequence data from GenBank. We aligned sequences using ClustalW (v.2.1)126 with the default parameter settings and then used jModelTest2 (v.2.1.10)127 to compare the fit of 44 models of sequence evolution to the sequence data. We then calculated pairwise genetic distances under the best-fit model (TVM + G), identified with AICc scores, using MEGA X (v.10.1.7)128. We then followed the same steps as for the R. granulosa data, except that we used all 19 WorldClim variables. Our sample size was reduced to 31 because three sampling sites fell within masked LSP pixels. The results are visualized in Fig. 4b (bottom).
Allochrony by allopatry: coffee harvest
To test for significant agreement between the harvest season map produced by the National Federation of Coffee Growers of Colombia (Federación Nacional de Cafeteros de Colombia, or Fedecafé) and our LSP map, we constructed a permutation-based test of an index of similarity between the harvest categories in the Fedecafé map and the categories resulting from clustering on NIRV phenocycles. First, we used WebPlotDigitizer98 to digitize and save a set of sampling points within each of the four harvest season colours displayed in a previously published Fedecafé map54. Next, we used Python to extract NIRV phenocycles at all unmasked pixels coinciding with those points and then used k-means clustering to cluster all extracted phenocycles into four clusters. We then calculated the Jaccard index129 of this cluster assignment vis-a-vis the Fedecafé harvest season assignment as:
$$J={n}_{{rm{both}}}/({n}_{{rm{Fedecaf}}{rm{ acute{{rm{e}}} }}}+{n}_{{rm{LSP}}}+{n}_{{rm{both}}}),$$
where nFedecafé is a count of pairwise point comparisons that have the same assignment only within the Fedecafé map, nLSP is a count of those that have the same assignment only within the LSP clustering and nboth is a count of those that have the same assignment in both datasets. Finally, we executed the same operation 1,000 times, each time first permuting the relationship between the sampling points and their phenocycles, generating a set of null J values against which to calculate an empirical P value for the observed J value (as the fraction of the 1,000 simulated J values that are at least as large as the observed J). We visualize the overall agreement between the Fedecafé map and ours by plotting sampling points on top of the RGB composite from the LSP EOF analysis (but not transformed across the ITCZ, given the colour-warping this causes within this region) and using colour to match the harvest season assignments of the sampling points to a series of line plots of their median, 10th percentile and 90th percentile phenocycles in our dataset (Fig. 4c).
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.