In 2025, many Hollywood unions are facing existential questions about how to survive in a rapidly changing media environment. As film and television studios consolidate and cut costs, opportunities are diminishing for organized labor in…
Based on multibody dynamics (ADAMS2020, https://hexagon.com/products/product-groups/computer-aided-engineering-software/adams) integrated with full-well drill string dynamics theory, comprehensive drill string assembly modeling, rate of penetration (ROP) model, and reamer force analysis model from the top drive to the bit were established.
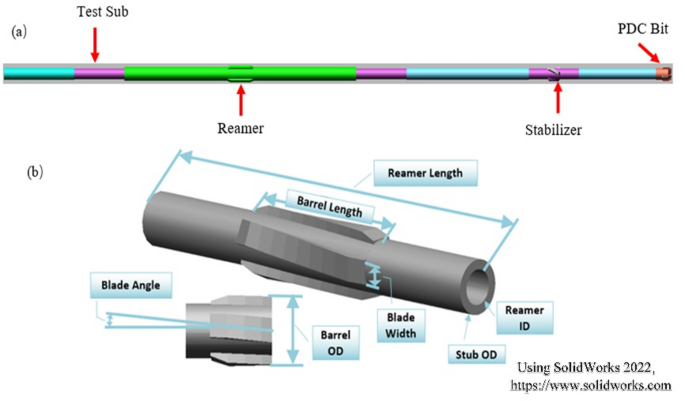
A well in Dagang Oilfield was selected as the case study, with the drill string assembly configuration: PDC bit + double box sub + Stabilizer + float valve with crossover sub + crossover sub + reamer + testing sub + 42 sections of heavy-weight drill pipe + 372 sections of drill pipe. The distance between the bit and the reamer is 6.9 m, and the bit depth is approximately 3993 m. The established reamer model primarily considers its tool body length, OD and ID, as well as the length, orientation angle, and outer diameter of the blades. Figure 1 shows the reamer geometric model and the BHA model.
(a) BHA model. (b) Reamer Geometric Model.
Since rock-breaking simulation is not included in the dynamic simulation, the ROP (rate of penetration) must be modeled using a nonlinear spring-damping function. During the hypothetical rock-breaking process, an axial load acts between the wellbore wall and the reamer, while the wellbore wall interacts with the formation via spring and damping forces. Based on Newton’s second law, the bottomhole dynamic equation is formulated as Eq. (1), the ROP response is shown in Fig. 2, where Fig. 2(a) represents the theoretical calculation of ROP and Fig. 2(b) depicts the software simulation response of ROP:
$$mS^{primeprime}+cS^{prime}+kS=Kleft( {ROPcdot t+{c_R}} right)+ccdot ROP+{F_b}left[ {a+vcdot sin (omega t)} right]+mg$$
(1)
where m is the mass of the wellbore wall (kg); c is the damping coefficient of the wellbore wall (N/(m/s)), change with well depth; k is the spring stiffness coefficient of the wellbore wall (N/m), change with well depth; g is gravitational acceleration (m/s²); ROP is the mechanical rate of penetration at the bit (m/s); CR is the initial condition for the differential equation governing the ROP input parameter at the bit; Fb is the amplitude of the sinusoidal WOB fluctuation load (kN); a is the constant coefficient term in the sinusoidal WOB fluctuation load.
(a) Represents the theoretical calculation of ROP. (b) Depicts the software simulation response of ROP.
The WOB model is constructed using the STEP, VARVAL, and DIF functions in Adams, Eq. (2)~3: the input WOB is introduced into the hookload function via the STEP function, where the hookload function is defined as the sum of the step function of WOB and the integral of the hookload differential function. The hookload serves as the external load applied to the spring-damping dynamics model of the upper drillstring axial system, while the lower end of the upper drillstring axial system is coupled with BHA through spring-damping elements.
$$WOB=STEP(Time,85,0,120,50000)$$
(2)
$$Hookload= – DIF(HookloadLatch)+VARVAL(WOB)$$
(3)
HookloadLatch denotes the hookload differential function:
$$begin{gathered} HookloadLatch=IF(MODE – 5:0, – DIFleft( {HookLoadLatch} right) – 1E7* hfill \ left( {DZleft( {Drillpipe,Bit,GCS} right) – 317.5948141401} right),0) hfill \ end{gathered}$$
(4)
In the equation, MODE denotes the decision parameter, where Drillpipe and Bit represent the positions of the drillpipe and bit along the Z-axis in the coordinate system, and GCS denotes the global coordinate system (GCS).
The rock-breaking process is not simulated in the dynamic calculation; hence, a cutting tooth and gauge tooth rock-breaking model is established to simulate this process. During model construction, it is assumed that each cutting tooth on the blade bears an equal WOB. Based on the azimuthal angle and tooth center radius, the equivalent load position on each blade is calculated using the equivalent torque method. Loads are applied to the equivalent teeth to simulate rock-breaking, with the derived functions defined in Eq. (5)~7 and the load application illustrated in Fig. 3.
$${F_{cut{kern 1pt} {kern 1pt} axial}}=IMPACT(DZ({h_z},{c_{z1}},GC{S_h}),VZ({h_z},{c_{z1}},GC{S_h}),0.5,1.0E5,1.05,500,0.005)$$
(5)
$${F_{cut{kern 1pt} {kern 1pt} tagent}}=mu cdot IMPACT(DZ({h_z},{c_{z1}},GC{S_h}),VZ({h_z},{c_{z1}},GC{S_h}),0.5,1.0E5,1.05,500,0.005)$$
(6)
$$begin{gathered} {F_{Gauge{kern 1pt} {kern 1pt} radial}}=IF(DX(reamer_O{D_x},{g_{x1}},GC{S_g}) – 0.6083:0,0,1.0E5cdot hfill \ {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} ABSleft( {DXleft( {reamer_O{D_x},{g_{x1}},GC{S_g}} right) – 0.6083} right)**1.05+ hfill \ {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} STEP(DX(reamer_O{D_x},{g_{x1}},GC{S_g}),{kern 1pt} {kern 1pt} {kern 1pt} 0.6083,{text{ }}0,{text{ }}0.6083 hfill \ {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} +0.005,{text{ }}500)*VXleft( {reamer_O{D_x},{g_{x1}},GC{S_g}} right){text{ }}) hfill \ end{gathered}$$
(7)
$$begin{gathered} {F_{Gauge{kern 1pt} {kern 1pt} tagent}}=mu cdot IF(DX(reamer_O{D_x},{g_{x1}},GC{S_g}) – 0.6083:0,0,1.0E5cdot hfill \ {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} ABSleft( {DXleft( {reamer_O{D_x},{g_{x1}},GC{S_g}} right) – 0.6083} right)**1.05+ hfill \ {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} STEP(DX(reamer_O{D_x},{g_{x1}},GC{S_g}),{kern 1pt} {kern 1pt} {kern 1pt} 0.6083,{text{ }}0,{text{ }}0.6083 hfill \ {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} +0.005,{text{ }}500)*VXleft( {reamer_O{D_x},{g_{x1}},GC{S_g}} right){text{ }}) hfill \ end{gathered}$$
(8)
The force interactions between the hole opener and wellbore wall components are modeled through kinematic joint constraints.
To validate the established dynamic model, a comparative analysis was conducted using vibration data from a Dagang Oilfield well during hole-opener drilling. The formation interval corresponds to the Guantao-Dongying Formation, with the drillstring configuration as described in Sect. 1.1. The comparison between simulated and measured results is shown in Fig. 4: Axial acceleration: The RMS value of the measured data is 0.152 g, while the simulated value is 0.126 g, deviating by 17%. Both exhibit similar waveform morphology; Rotational acceleration: The RMS value of the measured data is 26.247 rad/s², and the simulated value is 23.860 rad/s², deviating by 9%. The waveform characteristics also align closely. The model is validated as effective and suitable for parametric analysis of influencing factors.
Comparison between simulated data and measured data.
Mary Callahan Erdoes, Chief Executive Officer of J.P. Morgan Asset & Wealth Management, speaks during CNBC’s Delivering Alpha event in New York City on Nov. 13, 2025.
Adam Jeffery | CNBC
NEW YORK — Investors should be focused on opportunities ahead with artificial intelligence rather than whether there’s a bubble currently, according to Mary Callahan Erdoes, CEO at JPMorgan Asset and Wealth Management.
Speaking Thursday to the CNBC Delivering Alpha conference, Erdoes dispelled worries over valuation, saying that AI is presenting opportunities not fully appreciated or understood yet.
“I feel like we’re just on the precipice of a lot of this stuff,” she said during a panel discussion. “So we’re in this disconnect of the world is pricing where, where AI multiples should be. The companies haven’t gotten it through the usage. But it’s very much like Hemingway said, ‘How do you go bankrupt?’ It happens like very, very slowly, and then all of a sudden, and I think that’s exactly what’s going to happen AI.”
Worries over skyrocketing valuations for companies such as Nvidia, AMD and a multitude of other tied to the AI trade are causing repeated gyrations in markets, which nonetheless are still hovering around record highs.
Stocks sold off Thursday, registering their worst day in more than a month as fears once again bubble to the surface.
Michael Arougheti, Chief Executive Officer and a Director of Ares Management Corporation, speaks during CNBC’s Delivering Alpha event in New York City on Nov. 13, 2025.
Adam Jeffery | CNBC
“AI itself is not a bubble. That’s a crazy concept. .. We are on the precipice of a major, major revolution in a way that companies operate,” Erdoes said. “So if you say to yourself, is AI in a bubble, I feel you have to get very granular on how you’re going to answer that, because in the U.S., we’re starting to gain traction, but we’re nowhere near the ability to have the stuff all to the bottom line.”
“You’re going to see explosive growth on both the revenue and the expense side, and the suppliers of it are going to have to figure out how they make their way through the pipeline,” she added.
Erdoes was not alone in her assessment.
Michael Arougheti, CEO at Ares Management, said the level of investment now is meager compared to the potential that AI holds.
“We have a long way to go in terms of the economic investment relative to the size of the economy,” Arougheti said. “We can’t bring the supply on fast enough to meet the near term demand. So I just feel there’s a lot of hyperbole because the numbers are big and it is that revolutionary.”
Speaking on macro issues, Erdoes said she also doesn’t see a recession on the horizon.
“People have been calling for a recession now for five years, and it just hasn’t come,” she said. Speaking of credit investment, Erdoes added, “If there’s not a recession on the horizon, it’s a great buying opportunity, and you should be leaning in and buying.”
When the big shopping events like Prime Day and Black Friday come around, our sights are set on our favorite tech. It’s often the only time when they’re guaranteed to get a discount. My…
KYIV, Ukraine: European Union officials warned Ukraine on Thursday that it must keep…