- IT ministry sets dollar rate, terms for spectrum auction Dawn
- Govt warned against hasty 5G rollout Dawn
- 5G Auction Moves Closer in Pakistan as Government Issues Policy Directive 8171ip.com.pk
- Will 5G actually improve internet access for ordinary Pakistanis? Business Recorder
- Spectrum auction directive, a recipe for reform or revenue grab? Pakistan Today
Category: 3. Business
-
IT ministry sets dollar rate, terms for spectrum auction – Dawn
-
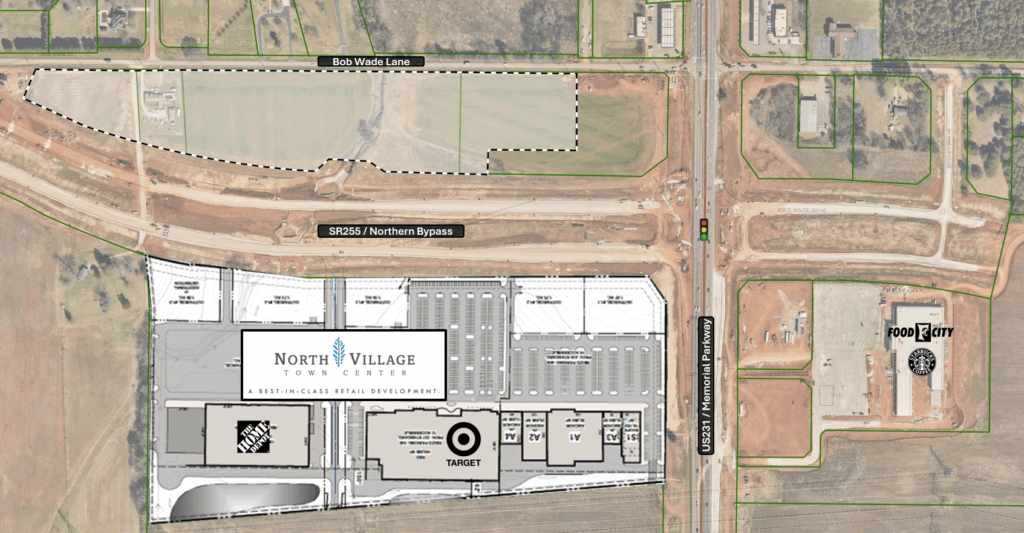
New North Huntsville shopping district moving forward
Published on January 8, 2026
Huntsville’s latest new retail district continues to expand and progresses towards construction later this year.
The City approved a contract with Schoel Engineering Company for engineering design and construction administration services for public infrastructure improvements related to the North Village Town Center project at Memorial Parkway and State Route 255 (Northern Bypass). The scope of work includes design and engineering services for general mass grading, utilities, and additional roadway improvements for the area.
The City last month announced the $240 million development, which will be anchored by Target and Home Depot. Upon completion, the project will consist of over 600,000 sq. ft. of new retail shops and restaurants.
On the northern side of State Route 255 directly across from North Village Town Center, the City also agreed to sell 15.23 acres of land to Hank Holdings LLC. The property will be developed to deliver additional retail and restaurant tenants to the North Huntsville retail district.
The City of Huntsville approved the land sale to Hank Holdings LLC on the north side of State Route 255 for retail and restaurant development.
Continue Reading
-

Fujitsu develops digital learning platform for JAL to support self-directed learning and training management
Fujitsu Limited today announced that it has jointly developed a new digital learning platform with Japan Airlines Co., Ltd. (JAL) to support educational training improvements at JAL’s airport sites. The platform, which leverages Fujitsu’s digital learning solution Advanced Teaming Experience Service powered by UMU, began full-scale operation in April 2025.
Since the initial roll-out, approximately 15,000 employees across roughly 100 locations across the JAL Group have adopted this platform which enables staff to conduct preparatory and review work on their assigned tablet devices. Furthermore, it has significantly reduced the workload associated with managing training participation and certifications, thereby contributing to enhanced productivity among frontline staff.
Fujitsu will continue to contribute to the JAL Group’s educational improvements through this platform. Furthermore, by applying the knowledge gained from this project, Fujitsu will continuously enhance Advanced Teaming Experience Service powered by UMU and actively promote its deployment not only in the aviation industry but also in other sectors requiring high safety standards and specialized expertise, such as manufacturing. Fujitsu remains committed to supporting organizations in maximizing the effectiveness of their educational improvements and human resource development initiatives by empowering their workforce through learning.
Continue Reading
-

Visa discusses digitising govt payments
ISLAMABAD:Minister for Finance and Revenue Senator Muhammad Aurangzeb on Thursday held a meeting with a Visa delegation led by Tareq Muhmood, Regional President for Central Europe, Middle East and Africa, to discuss advancing digital payments, financial inclusion and ongoing economic reforms in Pakistan.
Aurangzeb appreciated Visa’s continued engagement with Pakistan’s financial sector. The discussion focused on improving macroeconomic indicators, ongoing economic stabilisation efforts and the government’s priorities for achieving sustainable and inclusive growth, according to a news release.
Aurangzeb briefed the delegation on progress under the International Monetary Fund (IMF)-supported programme, external validation from international credit rating agencies and the government’s reform agenda. He outlined reforms covering taxation, the energy sector, state-owned enterprises, public debt management and privatisation, including recent steps taken to accelerate the privatisation process.
Both sides exchanged views on accelerating Pakistan’s digital transformation, with particular emphasis on strengthening digital infrastructure, payment systems and the digitisation of government payments. Aurangzeb said digitalisation is being led at the highest level by the prime minister to ensure coordinated and cross-government implementation.
He highlighted initiatives including the establishment of the Pakistan Digital Authority, reforms in payment rails under the State Bank of Pakistan and efforts to digitise government receipts and expenditures.
Continue Reading
-

OGRA moves to scrap fixed returns in gas pricing
SSGC, SNGPL resist shift as regulator begins stakeholder consultations; public hearing set for Friday
Gas utilities. Photo: file
ISLAMABAD:Following the government’s plan to restructure gas utilities, the Oil and Gas Regulatory Authority (OGRA) has decided to review the existing gas pricing formula based on return on fixed assets, keeping in view current gas sector dynamics and market liberalisation.
The government had tasked the OGRA with restructuring the two public gas utilities by doing away with the fixed asset-based return. According to officials, the regulator hired consultancy firm KPMG to review the formula, and it has submitted its report.
The regulator has started consultations with stakeholders to change the gas pricing formula and has scheduled a public hearing here on Friday to consider the views of stakeholders.
Since 2018, OGRA has been allowing a market-based rate of return to the gas utilities, namely Sui Northern Gas Pipelines Limited (SNGPL) and Sui Southern Gas Company (SSGC), on the value of their average net fixed assets in operation for each financial year.
OGRA said that, considering the latest gas sector dynamics, including demand and supply conditions, price volatility, market liberalisation and international benchmarking undertaken across the world, it has decided to review the existing gas pricing formula based on the rate of return (ROR) through an independent consultant, in line with the approved terms of reference.
“OGRA, after receipt of the first draft report as furnished by M/s KPMG, has decided to call a public consultation with all stakeholders as per its ToRs and the relevant legal provisions to ensure transparency and inclusive stakeholder engagement,” the regulator said.
The gas utilities are opposing the proposal to shelve the guaranteed asset-based return formula and have asked the government to continue with the current pricing regime.
The gas pipeline network continues to expand, resulting in higher gas prices and increased profits for the utilities, but this expansion has also led to gas shortages across the country. SNGPL’s operating cost surged from Rs66 billion in the financial year 2019-20 to Rs94 billion in 2023-24. At the same time, its earnings swelled from Rs19 billion to Rs38.9 billion, despite a drop in gas supply.
The utilities, SNGPL and SSGC, are of the view that the current asset-based return cannot be abandoned. They argue that several benchmarks, including unaccounted-for-gas (UFG), are linked to the asset-based return regime.
However, a number of industries have repeatedly criticised the fixed rate of return, arguing that the profits of the utilities are rising while gas supplies are shrinking due to continued expansion of the pipeline network.
At present, gas companies are facing a circular debt of Rs2.6 trillion, which has choked the entire energy chain. Liquefied natural gas (LNG) has been a major factor behind the accumulation of circular debt, as SNGPL has to pay billions of rupees for LNG supplies procured through Pakistan State Oil (PSO).
The present government has also opened the gas market by allowing gas utilities to allocate 35% of their gas to third parties. As a result, the regulator has received several applications from private parties seeking licences to market gas.
Oil and gas exploration companies had welcomed the government’s decision to increase gas allocation to private parties from 10% to 35%, saying it would help improve their cash flows by enabling them to secure better prices from private buyers.
The exploration companies are also facing cash flow constraints due to the circular debt issue and are of the view that the mounting debt has slowed the pace of their development projects.
Continue Reading
-
Financial Services Regulation Committee publishes private markets report – UK Parliament
- Financial Services Regulation Committee publishes private markets report UK Parliament
- TheWealthNet – A more cost effective and efficacious route to accessing private markets Pam Insight
- Peers warn ‘passive’ Treasury not aware of private credit risks City AM
- Fix Private Markets Before Small Investors Are Invited In The Information
Continue Reading
-
Synaptic Theory of Chunking in Working Memory
Working memory (WM) is hypothesized to be a distinct capacity for holding and manipulating multiple pieces of information, which is crucial for human cognitive abilities such as verbal communication, reading comprehension, and abstract reasoning [1–3]. Paradoxically, however, people typically cannot simultaneously hold more than four items in WM [4]. For example, repeating several words or digits is practically effortless and mistake-free, but for lists of five random words, people begin making mistakes [5–7]. How, then, are people able to process much larger streams of inputs, such as long passages of text or movies? One attractive idea is chunking, i.e., organizing several items into higher-level units [8–13]. Sometimes chunks are stored in long-term memory due to previous experience [14, 15], e.g., familiar expression like “Oh my God” or “Easier said than done” can be processed as a coherent unit rather than individual words. These pre-existing chunks could be thought of as having stable memory representations learned and consolidated over time, and could therefore be encoded and processed as a single item. However, conceptually more challenging is the phenomenon of spontaneous chunking, where novel combinations of items are grouped into separate units “on the fly”, as when a phone number is divided into chunks of 2-3 digits each, or words in a sentence are combined into units based on their syntactic role, such as “–a little boy–was dressed – in a green shirt”. Indeed, this sentence is much easier to remember than a random sequence of nine words. Surprisingly, a minor manipulation like introducing slight pauses between presentations of consecutive groups of items is enough to trigger chunking and the corresponding increase in capacity [16–19]. In this study, we addressed two interrelated questions inspired by the above considerations: how spontaneous chunking might emerge in the brain and what is (if there is one) the limit for the number of items that can be held in WM when spontaneous chunking is activated.
Neuronal mechanisms of WM and the origin of WM capacity are still under debate. While the most accepted theory assumes that WM is carried by persistent activity of item-specific neurons [20–23], we propose that a more economic and robust mechanism is to rely on short-term plasticity (STP) in item-specific synapses [24] (see [25] for a recent review of activity-silent WM). When several items are loaded into WM, rather than having all of the neurons persistently active, information could be maintained by periodic reactivations of the corresponding clusters in the form of population spikes [24, 26]. After each reactivation of a certain cluster, the recurrent self-connections in this cluster remain facilitated, allowing it to bounce back after a period of silence when other clusters activate. The largest possible number of co-active clusters, i.e., the WM capacity, is determined in this theory by the longest possible time between consecutive reactivations for each cluster, which in turn depends on STP time constants [26]. In the current contribution, we extend the STP theory of WM by including longer-lasting forms of facilitation, such as synaptic augmentation (SA) [27]. In [28], it was shown that due to its slow build-up, SA level in recurrent self-connections encodes the order of presentation of stimuli in WM. While SA does not significantly change the maximal possible number of coactivating clusters, i.e., the basic WM capacity, it allows the network to selectively switch some of the clusters off for a longer period of time, without fully erasing information about their prior activity from the recurrent selfconnections [28]. Here, we will show that SA enables consecutive chunks to be activated one after another by switching on and off specialized chunking clusters that serve as controls, and in this way enhance the effective WM capacity. In the next section, we demonstrate this mechanism in a simplified neural network model of WM and show how much WM capacity can be increased by chunking compared to the basic regime.
Network model of working memory and chunking
Following our previous work on the synaptic theory of working memory [24, 26, 28], we consider a recurrent neural network model (RNN) where memory items are represented by specific clusters of excitatory neurons coupled to a global inhibitory neural pool, see Fig. 1(a) and Methods Sec. A. The feedback inhibition is assumed to be strong enough such that at any given moment, only one excitatory cluster can be active. To simplify the model, we neglect the overlaps between the stimulus-specific clusters, such that each cluster µ can be described by a single activity variable corresponding to the average firing rate of the corresponding neurons at a given moment Rµ(t). Furthermore, we assume that all the recurrent self-connections are dynamic [29, 30], i.e., instantaneous synaptic efficacy depends on the pre-synaptic activity within a certain time window due to a combination of short-term synaptic depression and facilitation: J Self(t) = u(t)x(t)A [29], where A is the amplitude of the recurrent strength, u(t) is the current value of release probability, and x(t) is the current fraction of the maximal amount of neurotransmitter that is available for release.

Illustration of the hierarchical working memory model.
(a) Network architecture. Stimulus clusters and chunking clusters both have recurrent self-excitations (thick sharp arrows) and reciprocal connections to the global inhibitory pool (not shown). Chunking clusters have dense but weak connections to the stimulus clusters (thin blunt arrows in the background). (b) Effective network architecture after presentation. Activities in the network selectively augment connections between stimuli within chunks and the corresponding chunking clusters, effectively forming a hierarchical structure. (c) Dynamics of the recurrent self-connections. Upon the arrival of pre-synaptic inputs (top panel), the release probability u increases, and the fraction of available neurotransmitters x decreases (left axis of the middle panel). The amplitude of the recurrent strength A gradually increases with each reactivation of the cluster (right axis of the middle panel). As a result, the total synaptic efficacy of the recurrent self-connection J Self = uxA oscillates (bottom panel). Activity traces are taken from the first stimulus cluster from the top panel of (d) below. (d) Network simulation. The first three memories are colored in blue, and the other three memories are colored in green. Shades represent external input to the cluster. Top: Memories are loaded at a uniform speed; chunking clusters are not activated. Only four out of six memories remain active in the WM. Bottom: Slight pauses after chunks activate the chunking clusters, which inhibit the stimulus clusters presented before the pause. All memories are retrieved chunk-by-chunk in the retrieval stage. The full activity trace of the synaptic variables is presented in Fig. S1.
When the cluster’s activity is high, the release probability in the corresponding recurrent connections (u) increases above its baseline level U, constituting shortterm facilitation, and the fraction of available neurotransmitters (x) decreases, representing short-term depression (Fig. 1(c)). When the cluster activity is low, both u and x variables relax towards their baseline values with time constants τf and τd, respectively (Methods Sec. A). Such transient changes in the synapses are well observed in experiments and are reported to last on the order of hundreds of milliseconds to seconds [27, 29, 31, 32].
The RNN detailed in Methods Sec. A exhibits different dynamical regimes, depending on the STP parameters and external background input. In particular, as shown in [24, 26], at high background input level, there exists a persistent activity regime where clusters have sustained elevated firing rates corresponding to loaded memory items. As the background input is lowered, there exists a low-activity regime with cyclic behavior where items that were loaded into the network via external stimuli are maintained in WM in the form of sequential brief reactivations called population spikes [33]. As the number of loaded memories increases, the network eventually fails to maintain some of them, i.e., there is a maximal number of items that can be maintained in the WM, C, which depends on the synaptic-level parameters of the RNN [26].
In addition to short-term facilitation and depression, experiments observed longer-scale forms of synaptic facilitation in cortical synapses, called synaptic augmentation (SA), characterized by slow, compared to STP, build-up with activity and decay of tens of seconds [31, 32, 34–36]. We introduce SA as a small transient change in synaptic strength A that is strengthened from its baseline value due to cluster activity, similar to u, but with a much longer time constant τA ≫ τf [28] (see Fig. 1(c)).
The main modification of the current model compared to our earlier work is the introduction of distinct excitatory/inhibitory “chunking” clusters which serve to control the stimulus clusters. Both stimulus clusters and chunking clusters have recurrent excitatory self-connections. Each time the system receives a chunking cue (e.g., when there is a temporal pause in stimulus presentations), one of the chunking clusters is activated and quickly suppresses the currently active stimulus clusters, effectively grouping them into a chunk (Fig. 1(b)). Sub-sequent stimulus clusters are then free to be loaded into the network until the next chunking cue is received and another chunking cluster is activated. At the end of the presentation, only chunking clusters reactivate cyclically while all the stimulus clusters are inhibited (Fig. 1(d)).
Chunking increases working memory capacity
The main idea of the proposed chunking mechanism is that the chunking clusters can selectively activate and suppress the stimulus clusters, so that at no point in time do more than a small number of stimulus clusters reactivate as population spikes, thus not exceeding the basic WM capacity. Due to synaptic augmentation, stimulus clusters that are currently suppressed by the chunking clusters still have stronger recurrent self-connections than the ones that were not active at a given trial as long as augmentation has not disappeared. Therefore, the network can retrieve temporarily suppressed items by sequentially switching off the chunking clusters, releasing the suppressed stimulus clusters within the corresponding chunk from inhibition.
To demonstrate the chunking mechanism, we simulate a network of 16 clusters (both stimulus and chunking), 6 of which are activated consecutively with transient external input (presentation stage, the shades in Fig. 1(d)). We first consider continuous presentation of 6 inputs to the stimulus clusters with no chunking activated. At the end of the presentation, 4 of the corresponding clusters remain active in the form of periodic population spikes while two other clusters drop out of WM, corresponding to a WM capacity of 4 for the chosen values of parameters, similar to [26] (the top panel of Fig. 1(d)). Now consider presenting the same six memory items, but with a slightly longer interval between the presentation of the 3rd and 4th items, during which a chunking cluster is activated (shown in red in the bottom panel of Fig. 1(d)). We assume that the chunking cluster quickly inhibits the three stimulus clusters that were presented before it (the three blue colors) and remains the only cluster active until the items of the next chunk are presented to thenetwork (shown in green). A second chunking cluster is then activated, shown in purple. This way, the network effectively binds the stimulus clusters in each chunk to their corresponding chunking cluster (Fig. 1(b)). Such group-specific binding is akin to gating [37], where the activity of each chunking cluster gates the entire chunk of stimulus clusters via inhibition.
We assume that the fast inhibition between chunking clusters and corresponding stimulus clusters happens through strengthening the existing dense but weak inhibitory synapses between them (Fig. 1(a)). After all stimuli are presented, the network maintains reactivations of two chunking clusters while the synaptic variables of the stimulus clusters slowly decay to their baseline values. However, if the chunking cluster is suppressed within the augmentation time-window τA, the items that were inhibited by it will bounce back (Fig. 1(d) bottom panel, the blue colors in the retrieval stage). At this point in time, four clusters are active: the second chunking cluster and three stimulus clusters from the first chunk, with all items from the first chunk being successfully retrieved. When the second chunk is to be retrieved, the first chunking cluster is again activated by control input while the second chunking cluster is suppressed, allowing the stimulus clusters from the second chunk to activate. This chunking scenario allows the retrieval of all six memory items while at any given moment in time, the network maintains no more than four active clusters, not exceeding basic WM capacity. In this way, chunking increases effective working memory capacity by reducing the concurrent load on working memory, at the expense of activating higher-level representations (chunking clusters).
Above, we chose to illustrate the chunking mechanism in the periodic activity regime because the mechanistic effects of chunking clusters are most apparent with regular firing traces. Nevertheless, our proposed chunking mechanism applies to both the persistent-activity and periodic-activity regimes, with chunking clusters serving the same function in each. Note that, although we model the chunking cues here as slight pauses between presentations, in general chunking can be triggered by other cues, such as tonic variations and semantic meanings. The idea that chunking reduces the load on working memory was first introduced in the psychology literature [9, 14, 38]. Subsequently, neuroimaging studies observed that chunking reduces neural activity in upstream brain regions that process raw stimuli but increases activity in downstream regions associated with higher-level representations [18, 39, 40], which is consistent with our proposed mechanism.
Hierarchical chunking predicts a new capacity
Our model assumes that several stimulus clusters are grouped into chunks by chunking clusters. A natural question then arises: Can chunks also form meta-chunks? If so, is there a limit to how many levels of such hierarchical representations in working memory can be formed? Here we argue that the answers to both questions are affirmative and moreover, one can derive a surprisingly simple formula for the largest possible number of items in WM (Methods Sec. B):

where C is the basic WM capacity in the absence of chunking. As mentioned above, C corresponds to the number of active clusters that can be maintained in the RNN model (the top panel of Fig. 1(d) illustrates the case of C = 4), and it depends on all the synaptic-level parameters (Methods Sec. A)[26, 28].
Eq. (1) is a direct consequence of the limited amount of activity that the working memory network can sustain (Methods Sec. B) and does not depend on specific STP mechanisms. Therefore, we expect M ∗ to hold in working memory models with similar architecture but possibly different microscopic implementation from Methods Sec. A. Eq. (1) defines a new capacity for working memory that accounts for hierarchical chunking. Thus, we refer to M ∗ as the new magic number, in the original spirit of Miller [14].
Below we illustrate how the limited number of C clusters in the network constrains the total number of memory items that can be maintained and retrieved in WM. Let us consider the example corresponding to C = 4, with a capacity of M ∗ = 24−1 = 8. In this case, the optimal chunking structure is a binary tree with three levels (Fig. 2(a)).

Memory retrieval from a hierarchical structure.
(a) Top: Schematic of an emergent hierarchy of three levels. The top node (black) denotes the global inhibitory neural pool. The first two levels represent chunking clusters, and the lowest level represents stimulus clusters. Grey stripes denote the clusters that need to be suppressed to retrieve the 1st chunk. Blue dashed circles represent clusters that are active during the retrieval of the 1st chunk during the retrieval stage. Bottom: Architecture of the underlying recurrent neural network. (b) Simulation of the network in (a). R(k): activity trace of firing rates, color-coded to match the corresponding clusters in (a). The time-course of the traces is labeled as chunks (stimulus clusters), pauses (chunking clusters), and long pauses (meta-chunking clusters). Ib(k): activity traces of background input currents. Decreasing the background input to a cluster at level k suppresses its reactivation and removes the inhibition on its children clusters at level k − 1.
Eight memories are loaded as four chunks of two into the working memory network (the third panel in Fig. 2(b)): a slight pause in-between items of different colors (such as the 2nd and 3rd items) serves as the chunking cue to activate the chunking clusters (the second panel in Fig. 2(b)), which binds item clusters in pairs of two, similar to the chunks in the bottom panel of Fig. 1(d). However, here we introduce a slightly longer pause in-between the 4th and 5th items, during which a chunking cluster binding items 3 and 4 into a chunk is first activated, which is quickly followed by the activation of another chunking cluster to group the first two chunks into a meta-chunk (the first panel in Fig. 2(b)). In this way, after the presentation of the eight items, we have two meta-chunks, giving rise to a tree-like hierarchical structure of three levels (Fig. 2(a)).
To differentiate clusters at different levels of the hierarchy, we denote the ith stimulus clusters at the k = 3 level as


















As the retrieval begins (at t ≳ 8 s in Fig. 2(b)),








Experimental evidence for the existence of chunking clusters
Segmentation of sensory stimuli in human memory has been extensively studied in behavioral experiments from the early days of cognitive neuroscience and psychology [14, 15], but its neural correlates have not been explored until recently [18, 41, 43–45]. The key assumption in the hierarchical working memory model is the existence of chunking clusters that segment stimuli into chunks. Our model predicts that chunking reduces the load on working memory through inhibition. Upon the firing of the chunking clusters, we expect to see a decrease in the average firing rate of the stimulus clusters. Furthermore, as stimuli continue to be presented after chunking, the average firing rate should gradually increase after the drop. Overall, the hierarchical working memory model predicts two qualitative features in the firing rates of the cluster of neurons that encode stimuli (such as in the bottom panel of Fig. 1(d)): (1) there should be a “dip” in the activities of stimulus clusters upon the firing of the chunking clusters; (2) there should be a continuous “ramping-up” of activities following the dip.
Thanks to advances in single-neuron recording technologies, we can now test our hypothesis using data collected from drug-resistant epilepsy patients [41]. Consider the experiment reported in [41], where subjects are asked to watch a series of movie clips, each consisting of two episodes separated by a “cut” in the middle of the movie. Such movie cuts serve to induce cognitive boundaries for event segmentation in episodic memory. The authors in [41] identified a group of neurons in the medial temporal lobe that fire selectively at these boundaries and termed them “cognitive boundary” neurons. If these neurons segment episodic memories in a manner similar to how chunking clusters segment working memory in our model, then we should also observe a decrease in the firing rates of the stimulus neurons upon the firing of the cognitive boundary neurons. In [41], although the boundary neurons can be unambiguously identified by aligning their responses to movie cuts, it is difficult to pinpoint stimulus neurons due to the continuous nature of the visual stimulus. Therefore, we study the putative effect of boundary neurons on the rest of the system by aggregating neurons that are detected but not classified as boundary neurons. We align all the neurons to the movie cuts. Upon averaging over subjects and trials, we find that after the peak in the firing rate of boundary neurons (top panel of Fig. 3 (a)), about ~ 130 ms later, there is a dip in the average activities of the rest of the recorded neurons (bottom panel of Fig. 3 (a)). Further-more, there is a continuous ramp-up of activities following the dip. This trend is also evident at the level of individual subjects (Fig. 3 (b)), and qualitatively agrees with the prediction of our hierarchical working memory model. As a control, within the same recorded population we label the subset of neurons that respond to the onset of the movie clip as “onset” neurons. Aligning firing rates to the movie onset, we observe a peak in the on-set neurons as reported in [41]; however, unlike Fig. 3 (a), the remaining neurons (including boundary neurons) do not exhibit the dip-then-ramp pattern (Fig. 3 (c)). This indicates that the dip and ramp-up are specific to boundary neurons and suggests an internal network mechanism rather than simple inhibitory feedback or statistical artifacts.

Cognitive boundary neurons in the medial temporal lobe.
(a) Average firing rate from single-neuron recording data in [41]. The mean z-score firing rates are plotted in solid lines, with one standard deviation included as the shades. Firing rates are averaged over all subjects and trials, and the relative time zero is chosen to be the location of the movie cut. Two qualitative features in the firing rates of the non-boundary neurons: a dip followed by a ramp, are predicted by the hierarchical working memory model. Top: Boundary neurons. Bottom: Non-boundary neurons. (b) Average firing rates of non-boundary neurons over all trials for individual subjects. Subjects are sorted based on the location of the dip. A trend similar to panel (a) is observed for each subject. For individual 2D plots, see Fig. S3. (c) Average firing rates of neurons aligned to the onset of the movie (relative time zero). After the peak in onset-specific neurons, the non-onset-specific neurons do not exhibit the dip-then-ramp pattern seen in panel (a). Top: onset-specific neurons. Bottom: Non-onset specific neurons.
Experimental tests of the new magic number
An important prediction of the hierarchical working memory model is the existence of an absolute limit M ∗, beyond which perfect retrieval is impossible (Eq. (1)). One of the earliest studies to quantify this transition is the experiment performed by Miller and Selfridge [42] on the statistical approximation of language. In this experiment, the authors constructed n-gram approximations to English, where n refers to coherent occurrences with the previous n− 1 words. For example, a 1-gram approximation would consist of words randomly chosen from a corpus. In a 2-gram approximation, each word would appear coherently with the previous word, but coherence for any sliding window of three words is not required. As n increases, the constructed text gradually approaches natural text. In [42], subjects were presented with verbal materials constructed from such n-gram approximations and asked to recall the words. The fraction of recalled words f decreases with the length L of the material and increases with the degree of approximation n (Fig. 4(a) inset). Here, we are interested in the critical length Lc beyond which retrieval begins to be imperfect, i.e., f (Lc) = 1. Since the defining feature of working memory is the ability to perfectly retrieve items that are sustained in the memory, Lc is a measure of working memory capacity.

The new magic number bounds perfect-recall performance on verbal memory.
(a) Fraction of recalled words as a function of the length of the presented text. Different shades of blue correspond to different n-gram approximations. Black color represents natural text. Inset: Original data as presented in [42]. Main: Different n-gram approximation curves become straight lines in a semi-log plot and can be collapsed into a single universal curve (red dashed line) by adjusting the offsets on the individual intercepts. (b Critical length of perfect recall as a function of n-gram approximations. The location of the critical length Lc is determined by extrapolating the individual n-gram approximation curves to where f (Lc) = 1 using the universal slope. Different colored lines represent experiments in different languages. The grey dashed line corresponds to M ∗ = 2C−1 for C = 4.
In [42], the fraction of reported words for smallest stimulus length was less than one. To estimate Lc, we replotted the data from [42] in a semi-log plot (with f as a function of log2 L) and observed that all the different n-gram curves are well approximated by straight lines. We hence collapsed all the curves into a common line by adjusting the individual intercepts (red dashed line in Fig. 4(a)). We then used the slope of this line to extrapolate each n-gram approximation curve to its critical length Lc. We plot Lc as a function of n in Fig. 4(b). Lc increases with n as expected but starts to plateau around n = 4, saturating at roughly the predicted value of 8. Note that n = 0 corresponds to words randomly chosen from a dictionary, and is dominated by rare words many of which may not be familiar to the subjects. Therefore, the capacity for n = 0 is expected to be lower than that of common words as in the case for n = 1. The same analysis of two replicates of the Miller-Selfridge experiment in Danish and Hindi [46, 47] reveals similar trends. As n increases, the verbal material becomes more structured, which allows for the construction of hierarchical representations. Naively, one might expect that the number of perfectly recalled items Lc would continue to increase with n, as more structured materials are generally easier to remember. However, we observe that the performance plateaus around n ~ 4. This may be due to the fact that longer sentences need to be broken into smaller chunks to be stored in working memory, and there exists an optimal chunk size beyond which storage becomes inefficient and no longer improves memory. This observation qualitatively agrees with our theory in Eq. (1), and the value n ~ 4 at which capacity saturates could correspond to the size of a meta-chunk in the optimal hierarchical scheme illustrated above. Furthermore, our prediction that natural texts are chunked into pairs of two meaningful words resembles the empirical observation of collocations in language, such as adjective-noun, verb-noun, and subject-verb pairs, etc [48–51].
Notably, in Fig. 4(b) for all three languages, Lc saturates within the region predicted by M ∗ = 2C−1, when substituting for C = 4 [4]. Therefore, we conclude that the recall performance of verbal materials from working memory agrees with the prediction of our new magic number.
Chunking is classically believed to be a crucial process for overcoming extremely limited working memory capacity. In the current contribution, we suggest a simple mechanism of chunking in the context of the synaptic theory of working memory. The proposed mechanism relies on the ability of the system to temporarily suppress groups of items without permanently erasing them from WM, which is enabled by the longer-term form of synaptic facilitation, called synaptic augmentation. For chunking to work properly in the model, the system has to utilize separate neuronal clusters, which we call “chunking clusters” that effectively combine groups of several items each into distinct chunks. Moreover, the activity of chunking clusters has to be controlled in order to allow the suppression and reactivation of subsequent chunks at the right times to avoid saturating working memory capacity at any given moment. In particular, each chunking cluster has to be activated right after all of the corresponding stimuli are presented and later suppressed for them to be retrieved. Our model has no explicit mechanisms for this hypothesized control of chunking clusters; we speculate that it could be triggered by corresponding cues, e.g., chunking clusters could be activated by extra temporal pausing or intonation accentuation, and suppressed by internally generated retrieval signals. While further experimental and theoretical studies are needed to elucidate these suggestions, the existence of specialized chunking neurons has some recent neurophysiological support in electrical recordings in epileptic patients, where neurons responding to cuts in video clips were identified. We analyzed the data collected in these experiments and found that the activity of these and other neurons during clip watching is broadly consistent with our model predictions.
Apart from proposing the biological mechanism of chunking in working memory, we considered the question of whether the hierarchical organization of items in working memory could emerge from the subsequent chunking of chunks. Indeed, we demonstrated that the model allows for such a hierarchical scheme; however, due to working memory capacity, the overall number of items that can be retrieved is still constrained even for the optimal chunking scheme. We derived the universal relation between capacity and the maximal number of retrievable items, which we call a magic number following the classical Miller paper [14]. In particular, this relation predicts the new magic number of 8 for a working memory capacity of 4, which is currently accepted as the best estimate of capacity. The chunking scheme achieving this limit corresponds to dividing the inputs into 4 chunks of 2, with two “meta-chunks”, each consisting of two chunks. We reanalyzed the results of a memory study where subjects were presented with progressively higher-order approximations of meaningful passages for recall, and found that indeed the average maximal number of words that could be fully recalled was close to the predicted value of 8, and that this number saturated for a 4th order approximation of meaningful passages, corresponding to the size of a “meta-chunk” in the optimal chunking scheme predicted by the model. While encouraging, more studies should be performed to elaborate on this issue, in particular to more directly demonstrate the ability of subjects to form chunks of chunks during working memory tasks.
Our theory and the proposed neural network mechanism attempt to bridge the microscopic level of neural activities and the macroscopic level of behaviors in the context of hierarchically-structured memories. Our analytical results and data analysis methods offer new perspectives on classical results in cognitive neuroscience and psychology. The proposal of a hierarchical structure in working memory can open many new directions. For instance, long-term memory is usually organized in a hierarchical manner, as reflected in our ability to gradually zoom into increasingly fine details of an event during recall [52]. While working memory underlies our ability to construct such hierarchical representations, little is known about how the transient tree-like structure in working memory is related to the hierarchy in long-term memory. Furthermore, one of the hallmarks of fluid intelligence — the ability to compress and summarize information — is also related to re-coding information in a hierarchical manner [53]. Understanding how our mind is capable of making use of hierarchical structures for complex cognitive functions such as summarization and comprehension remains an important open question.
A. RNN model for hierarchical working memory
As illustrated in Fig. 1(a), the recurrent network that implements WM has 3 functionally distinct types of neuronal populations: stimulus clusters that encode different items (indexed by i below), chunking clusters (indexed by m), and a single inhibitory neural pool indexed by I. WM implementation is based on the previously introduced synaptic theory of working memory [24, 26, 28]. All stimulus and chunking clusters exhibit short-term synaptic plasticity in the recurrent self-connections, such that the instantaneous strength of connections for cluster µ (µ = (i, m)) is given by

where A is the amplitude of the recurrent strength, u is the probability of release, and x is the fraction of available neurotransmitters; all three factors depend on time via the following dynamical equations reflecting different STP processes:



where Rµ is the activity of cluster µ; U is the baseline value of release probability; τf, τd and τA are time constants of synaptic facilitation, depression and augmentation, correspondingly; Amin, Amax and κA are parameters of synaptic augmentation that distinguish this model from earlier versions. Apart from self-connections, each stimulus and chunking cluster is reciprocally connected to the inhibitory pool, and some of the chunking clusters develop quick inhibition on groups of stimulus clusters as explained below. The activity of each cluster is determined as a non-linear gain function of its input, and all inputs satisfy the following standard dynamics:


where R(h) = α ln(1+exp(h/α)) is a soft threshold-linear gain function mentioned above. Ib stands for external background inputs from other regions of the brain that reflect the general level of activity in the network, and Ie is the external input used to load memory stimuli. wEI and wIE define the strength of feedback inhibition between stimulus and chunk clusters and the global inhibitory cluster. Furthermore, we assume that when a chunking cluster m gets activated by a chunking cue at tc during the presentation, the weak inhibitory synapses are selectively strengthened between the chunking cluster and the stimulus clusters i in the same chunk presented before it:

See Fig. S1 for an illustration of the synaptic matrix before and after chunking. For the hierarchical structure in Fig. 2(b), we generalize Eq. (8) to higher-level chunking clusters, such that the kth level chunking clusters inhibit all the lower-level clusters presented before them (both chunking and stimulus).
The detailed synaptic mechanism for behavioral time scale plasticity such as Eq. (8) is subject to much active research [54–58]. Here in the RNN model, we do not attempt to explain its mechanism but rather assume that it takes place via external control. The microscopic implementation of Eq. (8) is not crucial to the proposed chunking mechanism, and in Methods Sec. D, we present additional RNN simulations that adopt a possible implementation of Eq. (8) and achieve similar activity traces as in Fig. 1(d) and Fig. 2(b).
B. The new magic number
At any given moment, the network cannot maintain more than C active clusters (Fig. 1(d) top panel illustrates the case of C = 4), and we refer to C as the basic working memory capacity. Even though we can potentially encode an arbitrarily deep hierarchical representation, C nevertheless constrains how many stimulus clusters can be retrieved. To understand the consequence of this constraint, we abstract away from the recurrent neural network and consider the effective hierarchical representation entailed by its activity (Fig. 2(a)).
Let us denote the size of the mth chunk at the kth level (1 ≤k≤ K) as ckm, which is the same as the branching ratio of its parent level. For example, the effective treelike hierarchical structure in Fig. 2(a) has four chunks of two stimulus clusters at the k = 3 level. It proves to be instructive to first consider a slightly simplified setting, where at a given level k all the chunk sizes are the same horizontally, ckm = ck for all chunks m (e.g., c2m = 2 for all four of the k = 3 level chunks in Fig. 2(a)). Later, we will relax this assumption and show that the result we derive below still holds.
To retrieve a chunk from the bottom of the hierarchy, i.e., the stimulus clusters that encode actual memories, we need to suppress nodes upstream of the desired chunk. As a result, children of the suppressed node will become reactivated. A series of suppressions from the top to the bottom of the hierarchy requires the working memory to simultaneously maintain cK stimulus chunks from the bottom level, as well as ck − 1 chunking clusters from each of the kth level above (1≤ k < K) that were not suppressed but become active due to the suppression of their parent. However, the total number of clusters that can be maintained must not exceed C (e.g., the total number of clusters enclosed by the blue dashed circles in Fig. 2(a) should not exceed 4),

Meanwhile, the total number of stimulus clusters encoded in the hierarchical structure is

To achieve maximum capacity, we maximize Eq. (10) subject to the constraint in Eq. (9). Using the arithmetic and geometric mean inequality, we arrive at

where the equality is saturated when the branching ratio (chunk size) ck at all levels are equal,

We notice that Mc(K) monotonically increases with K. Since the chunk size considered here ck needs to be an integer, we have the optimal level K∗ and optimal branching ratio c∗

Substituting Eq. (13) into Eq. (11), we arrive at the ca-pacity

Next, let us consider relaxing the simplifying assumption of ckm = ck. Without loss of generality, suppose that at the kth level, ck m> ckm+1. In order to retrieve the mthchunk at this level, the WM needs to at least maintainckm clusters, which implies that when trying to retrieve the (m + 1)th chunk the WM is not saturated because all the levels above the kth are identical for the mth and (m + 1)th chunk. This is sub-optimal since our goal is to maximize M. Therefore, ckm+1 can be increased to at least as large as ckm. The same logic can be applied recursively to all levels of the hierarchy, which demands that the optimal hierarchical structure for maximum M has ckm = ck, so we again arrive at M ∗ in Eq. (14).
C. RNN simulations
Activity traces of all the dynamical variables in Eq. (3)-(8) are shown in the Fig. S1. In particular, the synaptic matrix Jµv before and after chunking in Fig. 1(d) is shown for comparison. All simulation parameters are reported in Table I. All the external inputs Ie used for loading the memories are rectangular functions with support only at the presentation time, and have an amplitude of 750 Hz, and all the background input Ib has amplitude of |Ib| = 10 Hz. Additionally, the timing of the external control signals are summarized in below.
Fig. 1(d) top panel: Stimulus starts to load at t = 1 s for a duration of 0.025 s with an interval of 0.45 s. Background input Ib has a constant value of 10 Hz.
Fig. 1(d) bottom panel: Stimulus starts to load at t = 1 s for a duration of 0.025 s with an interval of 0.45 s. Chunking clusters are loaded for a duration of 0.025 s with an interval of 0.3 s. Background input Ib has a constant value of 10 Hz during the presentation stage and switches between 10 Hz and− 10 Hz for a duration of 1.35 s during the retrieval stage.
Fig. 2(b): The k = 3 level stimulus clusters start to load at t = 1 s for a duration of 0.15 s with an interval of 0.45 s. k = 2, 3 level chunking clusters load for a duration of 0.01 s with an interval of 0.2 s. Background input Ib has a constant value of 10 Hz during the presentation stage and switches between 10 Hz and− 10 Hz for a duration of 0.8 s during the retrieval stage.
D. Additional simulations
Eq. (8) assumes that chunking clusters can quickly bind with the stimulus clusters from the same chunk. For such binding to be selective, the synapse of the stimulus clusters need to be able to maintain a memory trace of its past activities. In this section, we attempt to provide a possible mechanism. We assume that there is a time-delayed Hebbian-like strengthening on the inhibitory synapses from the chunking clusters to the stimulus clusters. Such strengthening integrates back in time over a window τs (τf≪ τs ≪ τA) for stimulus clusters that were presented before the activation of the chunking cluster, and strengthens the originally present but weak synapses between them. Given a stimulus cluster i presented within τs before the chunking cluster m, the strength of the inhibitory synapses Jim between them gets strengthened according to

where

We expect Eq. (15) to work in the regime where the external input to the network during presentation is much stronger than the subsequent reactivations, which is typically the case. Here, the reactivations are filtered out so that they do not contribute to the binding process and form cross-linking between different chunks. Eq. (15) only strengthens the binding between the chunking cluster m and the stimulus cluster i that were presented within the τs time window, but not the stimuli that were presented outside of τs but reactivate during τs, which have much weaker amplitudes. As a result, the time-delayed augmentation effectively binds the chunking cluster with the stimulus clusters presented before it within τs. Time-delayed synapses were first introduced in the context of memory sequences [59–61], and are found to be related to behavioral time scale synaptic plasticity through dendritic computation [56, 57, 62].
As a potential detailed mechanism of Eq. (8), we perform additional RNN simulations with Eq. (15). We find that Eq. (6)-(3) with Eq. (15), instead of Eq. (8), is able to approximate the activity traces as in Fig. 1(d) and Fig. 2(b) (see Fig. S2). However, it requires fine-tuning between the presentation time and the integration window τs, as well as the threshold θ0. We report the additional parameters used in Eq. (15) below.
Parameters that are independent of the presentation times: τJ = 75 s, Jmin = 0, Jmax = 10, κJ = 1 Hz. Parameters that depend on the presentation times: Fig. S2) (a)-(b): τs = 1.8 s and θ0 = 7000 Hz. Fig. S2) (c): threshold θ0 is chosen to be proportional to the duration of the loading time with the external input: θ0 = 25600 Hz for J (2)⊣(3) and J (1)⊣(3), but for J (1)⊣(2) is reduced by a factor of five, where we use J (k)⊣(l) to denote synaptic matrix components that correspond to the inhibition from level k to l; Integration window τs is chosen such that adjacent levels are shorter than skip levels: τs = 1.9 s for adjacent levels (k = 1 to k = 2 and k = 2 to k = 3) and τs = 3.1 s for skip level (k = 1 to k = 3).
E. Cognitive boundary neurons
Two types of boundary neurons are reported in [41]: neurons that code for soft boundaries (change of camera position after the cut) and neurons that code for hard boundaries (change of movie content after the cut). In the present study, we do not distinguish between the two types of neurons and classify both as boundary neurons. In Fig. 3, we pool together the raw firing rates of all the boundary (or non-boundary) neurons from a subject, then perform the z-score averaging across different subjects. We have excluded four subjects out of eighteen in [41] from our analysis, because in those subjects either no neurons responding to the onset of the movie were detected, or no neurons responding to the onset of the cut were detected. The z-score firing rates of non-boundary neurons from individual subjects are shown in the Fig. S3. Data analyzed in Fig. 3 is downloaded from the DANDI Archive at https://dandiarchive.org/dandiset/000207/0.220216.0323.

Full activity trace of the bottom panel in Fig. 1(d).
(a) Activity traces of all variables. From top to bottom: firing rates Rµ, background input currents



Additional RNN simulations with delayed Hebbian plasticity.
(a) Approximating the chunking dynamics in Fig. 1(d) using Eq. (15) instead of Eq. (8). Top: activity traces of the firing rates. Bottom: activity traces of the inhibitory connections from chunking clusters to stimulus clusters JSC. (b) Snapshot of the synaptic matrix after chunking, resulting from the dynamics described in Eq. (15). (c) Approximating the chunking dynamics in Fig. 2(b) using Eq. (15) instead of Eq. (8). Synaptic matrix components that correspond to the inhibition from level k to l are collectively denoted as J (k)⊣(l). First three panels: firing rate activity traces of the clusters in Fig. 2(a). Fourth and fifth panels: inhibitory connections between adjacent levels J (1)⊣(2) and J (2)⊣(3), inhibitory connections between skip levels J (1)⊣(3), resulting from the dynamics described in Eq. (15).

Individual 2D plots of Fig. 3(b).
Individual subjects’ z-score firing rates of the non-boundary neurons are shown in blue, with one standard deviation included as shades. Black dashed lines denote t = 0 s where the movie cut occurs. Red dashed lines denote the location of the maximum firing rate of the boundary neurons. Results are pooled from the raw firing rates of all non-boundary neurons from that subject. Subject IDs are presented according to the data in [41]. While some subjects do not exhibit the qualitative trend as predicted (e.g., the firing rate of subject P64CS does not have a ramp, and TWH120 does not have a dip), most of the subjects’ firing rates follow the same qualitative trend as observed in the average plot in Fig. 3(a).
Continue Reading
-

Governor Moore Celebrates Major Terminal Enhancement at BWI Thurgood Marshall Airport – Press Releases – News
ANNAPOLIS, MD — Governor Wes Moore today opened Baltimore/Washington International Thurgood Marshall Airport’s Concourse A/B Connector and Baggage Handling System project. Opening for passenger and airline use tomorrow, the $520 million improvement project marks a major milestone in the airport’s commitment to support future growth and elevate the passenger experience. It is the largest capital project in the history of BWI Marshall Airport.
“We celebrate this project that will serve our passengers, support airline growth, and continue driving economic development for our state,” said Gov. Moore. “By modernizing our airport, we’re showing the world that we are making this Maryland’s Decade and committed to providing an outstanding travel experience for residents, businesses, and visitors.”
The Concourse A/B Connector and Baggage Handling System project includes a two-story building addition with 142,000 square feet of new construction and 78,000 square feet of renovations to existing space. The new in-line screening baggage handling system can process nearly 3,500 bags per hour – a significant increase over the previous 2,100 bags per hour. Planning for the project began in 2017, and construction officially kicked off in early 2022.
Southwest Airlines, the largest airline partner at BWI Marshall Airport, will utilize the new Concourse A/B Connector and Baggage Handling System. BWI Marshall Airport is one of the largest airports in the Southwest system, and the largest on the East Coast. The terminal enhancements offer Southwest Airlines added capacity to continue its growth at BWI. Southwest flew more than 18 million passengers at BWI Marshall in fiscal year 2025, with approximately 230 daily departures to 82 domestic and international destinations. The airline employs more than 5,000 employees in the BWI Marshall Airport market.
“This added gate capacity ushers the opportunity to add more service and prioritizes the airport experience for our Customers using BWI Marshall Airport,” said Southwest Airlines Chief Operating Officer Andrew Watterson. “Southwest launched our first international flights from here more than a decade ago; more recently, we welcomed our first cross-country redeye arrivals and connected our first interline Customers traveling overseas through BWI. We’re delivering more in 2026 with added comfort and choice, including assigned seating. Our longstanding partnership with the Maryland Aviation Administration positions BWI as much at the Heart of our future as it has in the decades we’ve served as the airport’s largest carrier.”
Key elements of the Concourse A/B Connector and Baggage Handling System Project include:-
A direct connection between concourses A and B, speeding passenger movements.
-
Five modernized, relocated airline gate areas featuring adjustable accent lighting, glass passenger boarding bridges, high-tech electrochromic glass for energy performance control, and comfortable new seating with integrated charging ports.
-
A sophisticated new in-line baggage handling system for Southwest Airlines that increases processing speed, improves reliability, and utilizes seven Explosive Detection System machines, with planned space for one additional machine.
-
Replacement of five existing, and the installation of one additional, baggage claim carousels. The new, modern equipment will improve baggage service and help meet future demand.
-
New state-of-the-art restrooms with upgraded lighting and clean technology to match the award-winning facilities in other parts of the airport.
-
14,000 square feet of open market space for new food and retail concessions, with an additional 28,000 square feet of shell flex space for future concessions.
-
Sustainability upgrades, including energy-efficient systems and environmentally responsible materials like glulam engineered wood beams that offer a lower carbon footprint than steel.
“As a vital transportation hub for Maryland, it is essential that BWI and its infrastructure is up-to-date to keep passengers safe and flights on time. This modernization project will help deliver a better travel experience for all from door to gate,” said Senator Chris Van Hollen.
“BWI Thurgood Marshall Airport is an indispensable nexus of commerce, culture, and travel in our state, and this new A/B Terminal Connector will make a marked improvement in the travel experience for both Marylanders and all those who wish to visit our state,” said Congressman Kweisi Mfume. “This project is a major step towards ensuring our state’s transit infrastructure is modernized, convenient, and able to handle the demands of a growing economy.”
“The Baltimore Washington International Thurgood Marshall Airport’s new A/B Terminal Connector is an exciting new investment here in the Third District that modernizes our airport and improves the traveler experience for Marylanders and visitors from around the globe,” said Congresswoman Sarah K. Elfreth. “The BWI airport has been a transit hub for 75 years, and I am thrilled to see this next phase of growth and connectivity.”
“The opening of the A/B connector is a major milestone for BWI Marshall Airport and for Maryland’s future,” said Maryland Department of Transportation Acting Secretary Kathryn Thomson. “This project strengthens BWI’s role as one of Maryland’s key international gateways—supporting economic growth, innovation and global connectivity—while delivering a more efficient, convenient experience for passengers and meeting the evolving needs of our airline partners.”
BWI Marshall Airport serves as a vital travel hub for Maryland and the National Capital region, connecting travelers to destinations around the globe. The airport offers approximately 300 daily nonstop departures to about 90 domestic and international destinations. BWI Marshall Airport generates a total economic impact of $11.3 billion annually. The airport and visitors produce and support more than 107,000 jobs throughout Maryland and the region.
“This multi-year project is a major investment that will shape the future of the airport for years to come,” said Baltimore/Washington International Thurgood Marshall Airport Executive Director and Chief Executive Officer Shannetta Griffin. “We are excited to welcome our customers into a brighter, more efficient and more modern terminal.”###
Continue Reading
-
-

Govt fixes dollar rate, shifts to KIBOR for 5G
ISLAMABAD:The Ministry of IT and Telecom has acknowledged long-standing demands of the telecom sector by easing payment terms and fixing exchange and interest rates in its policy directive for the upcoming next-generation mobile spectrum auction, a move that clears the way for the Pakistan Telecommunication Authority to issue the Information Memorandum for existing operators and new entrants to participate in the process.
Under the approved framework, the spectrum fee has been denominated in US dollars, but the exchange rate will be calculated at the National Bank of Pakistan’s TT selling rate prevailing at the close of business on the day preceding the auction date. At least 50% of the spectrum price will be payable within one year of the licence issuance date, while the remaining 50% will be paid in five equal annual instalments carrying interest at the KIBOR offer rate plus three percentage points.
The directive also revises the benchmark used for deferred payments. Unlike the 2021-era policy that linked instalments to the London Interbank Offered Rate, the current framework shifts to a domestic interest rate structure, a change sought by operators amid global rate volatility. Each new spectrum licence will be valid for a period of 15 years.
According to the policy, the PTA will auction multiple frequency bands, including 15 MHz of paired spectrum in the 700 MHz band, 3.6 MHz paired in the 1800 MHz band, 20 MHz paired in the 2100 MHz band, and unpaired spectrum of 50 MHz in the 2300 MHz band, 190 MHz in the 2600 MHz band, and 280 MHz in the 3500 MHz band. Base prices range from $6.5 million per MHz for paired 700 MHz spectrum to $0.65 million per MHz for unpaired 3500 MHz spectrum.
At the same time, the IT ministry has sought federal measures, in consultation with stakeholders, to address industry concerns. It proposed tax reductions to promote local manufacturing of 5G smartphones and duty-free imports of 5G equipment to accelerate adoption. The ministry also recommended industrial power tariffs for telecom operators through a joint task force.
Continue Reading
-
(Re)Empowering Fiduciaries in Proxy Voting
Good afternoon.
Thank you, Vadim [Avdeychik] for that kind introduction.
Before I begin, I must – as always – inform you that my remarks today are provided in my official capacity as the Securities and Exchange Commission’s Director of the Division of Investment Management, but do not necessarily reflect the views of the Commission, the Commissioners, or other members of the staff.
I will also point out that, while I will be speaking for about 10 minutes straight, I do have on my hippopotamus cufflinks. If you follow my social media or read my last speech, you know what that means and I hope that, after these prepared remarks, I can do more listening than talking.
That being said, it’s a privilege to be here today to speak with you about a topic that is current and consequential in our regulatory landscape: proxy voting by registered investment advisers.
A Thumbnail History
Many practitioners trace today’s proxy voting practices to the Department of Labor’s 1988 “Avon Letter,” which asserted that “the fiduciary act of managing plan assets that are shares of corporate stock includes the voting of proxies” and that proxy voting determinations by pension plan managers are fiduciary acts that must be made for “the exclusive benefit of plan participants.”
Read on its face, this is not a particularly controversial position. Is anyone really going to say that a fiduciary should not be voting a client’s shares for anything other than the client’s benefit?
However, this common-sense position on conflicts of interest (which was picked up by the SEC and enshrined in our 2003 proxy voting rule) metastasized over time across the regulatory landscape. While it took a few decades, investment adviser proxy voting policies now almost universally reflect the coupled mantras of “votes have value” and “we will vote all proxies.”
This created a lucrative business opportunity for proxy advisory firms. Proxy advisors scaled their product offerings from limited-scope, non-discretionary research to today’s end-to-end proxy voting “solutions,” which not only handle the mechanics of the voting process, but provide substantive “recommendations” on corporate policy matters that can effectively become industry-wide fiats.
This evolution gave rise to a small oligopoly of proxy advisory firms with de facto power to impose their views on social and political matters upon a large portion of the American capital markets. In short, proxy advisors have acquired the ability to influence corporate policy and public company management, without having to buy a single share of stock, and have done so over time under the cover of a fundamental regulatory tenet that votes must be made in the best interest of the client.
And who pays the price for this dysfunctional system? Well, no surprise here, but it is the investor, often the retail American investor, who ultimately pays the price.
In the interests of transparency, I will save you industry veterans the trouble of having to point out that the SEC contributed to this situation. Our past actions, even if undertaken with the best of intentions, may have contributed to investment advisers viewing proxy advisory services as a de facto regulatory safe harbor, as well as the most economically efficient way to operate in a “vote all proxies” environment. We even provided something of a road map through a series of – now-withdrawn – no-action letters that indicated investment advisers could avoid their own conflicts of interest by “outsourcing” their voting duties to proxy advisors,[1] but we did not step in quickly enough when this practice extended – in many cases – to ordinary course voting.
An Opportunity to Reset
But I don’t want to focus on the past this afternoon. Instead, I would like to focus on how we should be empowering investment advisers to reconsider their proxy voting policies and processes.
Unless you were on a desert island for the past year, you have undoubtedly noticed that proxy voting is a focus of the SEC’s overall regulatory agenda. Among other steps:
- Last April, under Acting Chairman Uyeda, our colleagues in the SEC’s Division of Corporation Finance rescinded Staff Legal Bulletin No. 14L and reiterated the Commission’s longstanding view that a public company should look at its specific business circumstances in permitting or excluding shareholder proposals.
- In October, Chairman Atkins called to “de-politicize shareholder meetings” and shift the focus back to director elections and significant corporate matters.
- And in November, CorpFin halted substantive reviews for most exclusions of shareholder proposals, limiting its review of requests for no-action to proposed exclusions based on state law.
But a seismic shift came a few weeks ago, when President Trump issued an executive order[2] addressing the influence that proxy advisors and their related consultancies wield to promote “radical politically-motivated agendas.”
That E.O. directs the SEC Chairman to consider several points, including:
- Whether to require proxy advisors to register with the SEC as investment advisers;
- Whether to require proxy advisors to provide increased transparency on their recommendations, methodology, and conflicts of interest, especially regarding “diversity, equity, and inclusion” and “environmental, social, and governance” factors;
- If and when the common use of a proxy advisor by investment advisers results in the formation of a Section 13(d) group; and
- Examining whether registered investment advisers engaging proxy advisors to advise on (and following the recommendations of such proxy advisors with respect to) non-pecuniary factors (including DEI and ESG factors) is inconsistent with their fiduciary duties.
Obviously, this is a big assignment – stay tuned for how we address it.
Proxy Voting Policies and Processes
With that backdrop, I thought that it might make sense to share my thoughts on the proxy voting landscape. And, again, I will remind you of my opening disclaimer – I am speaking only for myself in my capacity as director here.
I often hear investment advisers say that they feel compelled to vote on matters they do not deem important to their investment programs and that they would welcome more clarity that they need not vote all proxies. Many investment advisers engage a proxy advisor and let the proxy advisor’s recommendations serve as the investment adviser’s default voting instructions. The investment adviser can override the default, to be sure, but we all know how much effort it takes, in any situation, to override a default setting.
It also appears to me that many investment advisers would welcome a broader consensus on the answers to two basic proxy voting questions:
- Must I vote client proxies?
- If I elect to – or am required to – vote, can I (or “must I?”) still use a proxy advisor?
Question 1: Must I Vote Client Proxies?
If you look into this topic, the widespread, but superficial, view is that an adviser must vote client proxies. In fact, in the 2003 adopting release for the SEC’s proxy voting rule, the Commission stated that the fiduciary duty of care requires an adviser “to monitor corporate actions and vote client proxies.”
However, in that same paragraph, the Commission also stated that “We do not suggest that an adviser that fails to vote every proxy would necessarily violate its fiduciary obligations.” The Commission, rather, pointed out that:
There may even be times when refraining from voting a proxy is in the client’s best interest … [such as] where the adviser determines that the cost of voting the proxy exceeds the expected benefit to the client.
The Commission’s June 2019 Fiduciary Interpretation[3] stated the position that an adviser and its client may vary their fiduciary relationship by agreement, “provided that there is full and fair disclosure and informed consent.” In considering how this applies to proxy voting, the Commission went out of its way not to reduce the scope of an adviser’s discretion, simply stating that the release “does not address the specifics of how an investment adviser might satisfy its fiduciary duty when voting proxies.”
But, two months later, the Commission issued guidance on proxy voting considerations, stating that:
the client and the investment adviser may instead agree [that] … the investment adviser would only assume the authority to vote on behalf of the client in limited circumstances or not at all.
The Commission then provided two pages of examples of permissible arrangements to limit or eliminate an adviser’s obligation to vote proxies.
Not voting makes sense in many situations. Look, for example, at quantitative and systematic managers, who often operate models that merely seek exposures to identified sources of alpha. Many investment advisers managing quantitative and systematic strategies will even say that voting on board members, management policies, or on precatory social and political matters is irrelevant to their strategy and imposes costs without conferring any measurable benefit to investors. Yet many systematic managers continue to vote proxies (often using a proxy advisor’s default settings) because it is perceived as being “safer” than not voting.
Index funds present an interesting situation. Many mutual funds and ETFs purport to track a reference index, and the core mandate for the investment adviser is to replicate the performance of the reference index in the fund. No more, no less. But many index funds, like some systematic funds, vote proxies, notwithstanding their passive investment mandate. I suspect that some (perhaps many) of these investment advisers vote proxies – often according to some formula created by or in conjunction with a proxy advisor – because they feel pressured or obliged to do so. But it may be appropriate for these categories of investment advisers (and the Boards that exercise oversight over this function) to consider whether taking positions on fundamental corporate matters, or on precatory proposals, is consistent with their investment mandates.
But I do not want to leave you with the impression that I think that voting is not important. Because, for the overwhelming number of investment advisers, it is.
Fundamental managers can and generally should be voting on fundamental corporate matters. It would be unusual, absent a conflict of interest, for an activist, a private equity, or a venture fund manager not to vote on matters involving a portfolio company. I would think that traditional fundamental managers are in the same boat, at least for their core positions.
And investment advisers to passive or systematic strategies may deem some kind of neutral (or neutral-ish) voting policy to be essential for quorum and similar reasons.
So, there is no stock answer to the “Must I vote?” question… Instead, it is important that advisers and clients have a fair amount of latitude to decide what works in their individual cases.
Question 2: How Must I Vote?
This is an easy one to answer, at least at a certain level of abstraction: An adviser is a fiduciary and should cast ballots in the client’s best interests, on an informed basis.
In terms of how to get there in the real world, questions on how much of the deliberative process can be outsourced to proxy advisors are frequently raised. That’s a good question to ask, but one that, in my experience, winds up being situationally dependent. So, as a general principle, I think that we regulators should let advisers and clients have the first crack at deciding that.
Because when we do—when we step out of the way of market participants—innovation flourishes. Take, for example, those fund managers—including index fund managers—who right now are spearheading programs that enable their investors to express their voting preferences and direct their proportionate share of voting power. This is exactly the type of innovation we don’t want to inadvertently slow down: so long, of course, as they offer investors a sufficient number of options, accompanied by clear disclosure as to how shares would be voted under those options.
And let me be clear: there is nothing inherently wrong with an investment adviser using a proxy advisor. When operating pursuant to specific instructions within a tailored mandate and subject to periodic review, a proxy advisor can provide valuable research, analysis, and logistical support to an investment adviser.
But shouldn’t clients and investors be concerned when an investment adviser’s track record on non-routine matters is nearly identical to a proxy advisor’s standard voting policies and positions? In such a case, are clients and investors benefitting from the investment adviser’s expertise? And are the votes cast in the best interest of clients? Again, the answers will differ in each individual situation, but this is a topic that might be worth a review.
And if we are raising issues for consideration, I will also mention, because the President did, that there is real concern out there that habitual adherence to a proxy consultant’s recommendations could pull an adviser into a Section 13(d) group.
So Where Do We Go From Here?
“Here” is pretty clearly an unsatisfying locale.
“Here” is a place where retail and institutional investors are directly and indirectly supporting a system where an oligopoly of proxy advisors exercise influence over voting decisions for a large portion of the investment management industry. What happens “here” contributes to the de facto imposition of external political and social ideologies on US-listed public companies through the proxy voting process.
But we do not have to stay “here.”
Proxy voting should not be a rote box-checking exercise. It is a discretionary act within a relationship of trust that can influence corporate behavior, shareholder value, and client outcomes. A fund manager should be free to ask itself tough questions and to act in accordance with the honest answers.
Investment advisers that determine proxy voting is not required by, or may even be inconsistent with, their investment program should not be afraid to take that position. Assuming that such a determination is consistent with all relevant client agreements and is effectively disclosed to investors – and, of course, otherwise satisfies the adviser’s fiduciary duties of care and loyalty – I would find it hard to second-guess the adviser and the client.
Investment advisers that do vote, on the other hand, should be empowered to utilize their best judgment and whatever resources they deem appropriate under the circumstances when making that vote. At the same time, to the extent that the underlying investment mandate seeks passive exposure, those advisers should (re)confirm that they are comfortable with their authority to vote, both as a general matter and, in particular, when a vote reflects an investment adviser’s or a proxy advisor’s personal view or opinion on a social or political matter.
And in assessing proposed votes, investment advisers might utilize the Fiduciary Interpretation’s concept of a “reasonable inquiry into the client’s objectives.” If an investment adviser routinely follows a proxy advisor’s stock recommendations without a tailored engagement or independent analysis, is this “reasonable inquiry?” Maybe, but it is certainly worth thinking about. And, to go back to the first question, if the voting process is so burdensome that it requires extensive external resources, why is the adviser voting at all?
Is AI the (AN) Answer?
Finally, I want to insert a plug for artificial intelligence.
As advisers grapple with the scale and complexity of proxy voting—especially across large portfolios—AI tools like large language models and agentic AI, offer a compelling opportunity.
Imagine an AI agent that can review dozens or hundreds of proxy statements, assess them against your expressed values, and efficiently generate a large quantity of principled voting recommendations. And, pretty much, for free. This isn’t science fiction—it’s a near-term reality.
Of course, with great power comes great responsibility. AI agents need to be trained and their output needs to be reviewed. Any adviser’s use of AI in proxy voting would also need to take into consideration principles of transparency, auditability, and consistency with fiduciary duties.
But done right, AI can be a valuable tool that enhances—not replaces—human judgment, and that helps advisers better serve their clients.
In Conclusion
In conclusion, if you are an adviser and you and your clients are content with your tailored proxy voting arrangements, great. I am not here to force you to change your approach.
But if you are dissatisfied with your current proxy voting arrangements, or if you have not reconsidered them in a while, this is a great time to re-evaluate and reassess – and perhaps to redirect.
And to the extent that you find that Division or Commission action would be helpful, please give us a call or come in for a chat. And if you want to chat on the matters flagged in the President’s Executive Order, we are all ears.
Thank you for your time, and thank you for your continued commitment to serving investors with excellence and accountability.
Continue Reading